91

x

1

&

1

S

&

y

&

1

z

P

&

&

Рис. 3.6

Сложность (размер) схемы из функциональных элементов – это число функциональных элементов в этой схеме.

Приведённая на Рис. 3.6 схема имеет сложность (размер) 9.

§ 21. Функциональная декомпозиция

Пусть задана произвольная булева функция f(x1,x2,...,xn). Обозначим Х= (x1,x2,...,xn), тогда исходную функцию можно записать: f(Х).

Декомпозицией булевой функции f(Х) называется представление ее в виде f(Х)=g0(Х0,g1(Х 1),...,gk(Хm)),

где k≥1, m≥1, Хi - некоторое подмножество множества переменных Х, т.е. Хi = ( xi1 , xi2 ,...,xik( i ) ) , 1≤ ij≤ n, , 1≤ j≤ k(i), 1≤ k(i)≤ n, 1≤ i≤ m; gl(Хi) - некоторая булева функция, зависящая от множества переменных Х i, 1≤ l≤ k, 1≤ i≤ m.

Рассмотрим пример. Пусть f(x,y,z)=x y&z; Х={x,y,z} ; Х0= {x}, Х1 ={y, z}. Тогда f(x,y,z) = g0(Х0, g1(Х1)) =g0(x, g1(y,z)), где g0(x,y) = x y, g1(x,y)=x&y.

В зависимости от введенных выше чисел m и k, а также от способа разбиения множества Х на подмножества Хi различают несколько видов функциональной декомпозиции.

Если булева функция f(Х) допускает декомпозицию при k=1 и m=1, т.е. f(Х)= g0(Х0, g1(Х 1)), то такая декомпозиция называется простой.

Число множеств Х i называется размерностью декомпозиции, а число k- кратностью декомпозиции. Размерность декомпозиции равна m+1.

Если декомпозиция выполняется при условии, что Х i∩Х j = для любых i, j, i≠j, то декомпозиция называется разделительной. Если хотя бы одно пересечение подмножеств Х i и Х j не пусто, то декомпозиция называется

неразделительной.

92

Подробно

рассмотрим

x1

двумерную

разделительную

x2

декомпозицию

кратности

один,

X0

f(X)

которая

является основой

при

исследовании

других

видов

xs

g0

декомпозиции. Пусть f(Х)= g0(Х0,

g1(Х1)),

Х0∩Х1= .

xs+1

Структурная

(функциональная)

xs+2

схема двумерной разделительной

X1

декомпозиции

кратности

один

g1

имеет

вид,

изображенный

на

xn

рис.3.7. Для этой декомпозиции

заданное

множество аргументов

разбивается

на

Рис. 3.7

непересекающиеся множества Х0

= (x1,x2,...,xs), Х1 =(xs+1,xs+2,...,xn).

Ясно,

что

возможны и

иные

разбиения Х на Х0 и Х1. Для выяснения возможности декомпозиции строится декомпозиционная матрица, входами для столбцов которой являются всевозможные значения Х1, а входами для строк - всевозможные значения Х0. На пересечениях строк и столбцов записываются значения функции f.

Рассмотрим пример построения декомпозиционной матрицы. Пусть имеем булеву функцию f1(x1,x2,x3,x4)=(x1≡ x4) x2&x3 и пусть Х0 = (x1,x4), Х1

=(x2,x3). Построим для этой функции сначала таблицу истинности.

x1	x2	x3	x4	f1(x1,x2,x3,x4)	f2(x1,x2,x3,x4)
0	0	0	0	0	1
0	0	0	1	1	1
0	0	1	0	0	0
0	0	1	1	1	0
0	1	0	0	0	0
0	1	0	1	1	0
0	1	1	0	1	1
0	1	1	1	1	1
1	0	0	0	1	1
1	0	0	1	0	1
1	0	1	0	1	0
1	0	1	1	0	0
1	1	0	0	1	0
1	1	0	1	0	1
1	1	1	0	1	1
1	1	1	1	1	1

= (x1,x4)

93

Теперь построим декомпозиционную матрицу для Х0 = (x1,x4) и Х1 =(x2,x3). Эта матрица для функции f1(x1,x2,x3,x4) имеет вид:

Х0 \ Х1	00	01	10	11
00	0	0	0	1
01	1	1	1	1
10	1	1	1	1
11	0	0	0	1

Можно доказать следующую теорему.

Теорема 3.25. Булева функция f(Х), зависящая от n переменных, допускает двумерную разделительную декомпозицию кратности один тогда и только тогда, когда декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х0 и Х1, содержит не более двух различных столбцов значений функций.

Из этой теоремы следует, что в рассмотренном примере функция f1 допускает требуемую декомпозицию, ибо декомпозиционная матрица имеет только два различных столбца значений функции f1 для заданных Х0

и Х1 =(x2,x3). Ясно, что имеем: f1(x1,x2,x3,x4)=g0(X0,g1(X1)),

где

g0(X0,s)=(x1≡x4) s, g1(X1)=x2&x3.

Рассмотрим ещё функцию f2(x1,x2,x3,x4)= x1&x4 (x2 x3) (x2≡ x3).

Положим, что Х0 = (x1,x4) и Х1 =(x2,x3). Значения этой функции приведены в записанной ранее таблице истинности. Тогда декомпозиционная матрица для f2(x1,x2,x3,x4) имеет следующий вид:

Х0 \ Х1	00	01	10	11
00	1	0	0	1
01	1	0	0	1
10	1	0	0	1
11	1	0	1	1

Построенная декомпозиционная матрица содержит три различных столбца значений функции f2 поэтому эта функция не допускает двумерную разделительную декомпозицию кратности один при заданных Х0 = (x1,x4) и Х1

=(x2,x3).

Двумерной разделительной декомпозицией кратности k функции f

является ее представление в виде:

f(Х)=g0(Х0,g1(Х1), g2(Х1),...,gk(Х1 )).

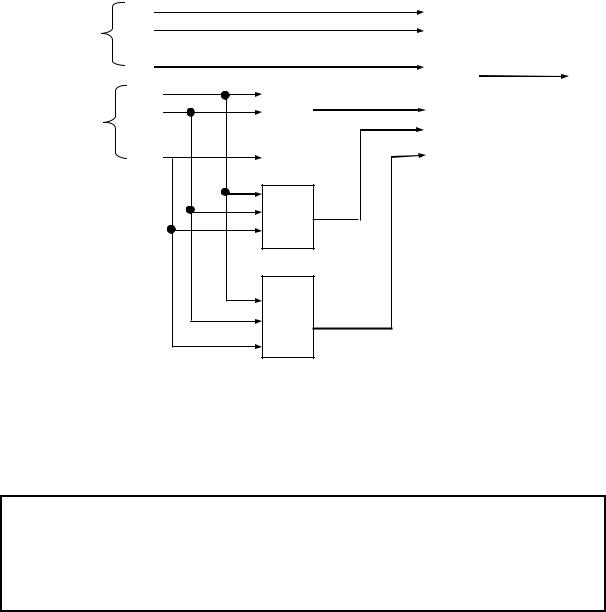
Структурная (функциональная) схема ее представлена на рис.3.8.

	94
x1
x2
X0
xs				f(X)
xs+1			g0
	g1
X1
xs+2
xn

g2

…

gk

Рис. 3.8

Можно доказать следующую теорему.

Теорема 3.26. Булева функция f(Х), зависящая от n переменных, допускает двумерную разделительную декомпозицию кратности k тогда и только тогда, когда декомпозиционная матрица функции f(Х), соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х0 и Х1, содержит не более чем 2k различных столбцов.

Для функции f2(x1,x2,x3,x4) = x1&x4 (x2 x3) (x2≡ x3) при Х0 = (x1,x4) и

Х1 =(x2,x3) её декомпозиционная матрица содержит три различных столбца значений этой функции, т.е. не более чем 22 различных столбца. Следовательно, f2 допускает двумерную разделительную декомпозицию кратности 2 для заданных Х0 = (x1,x4) и Х1 =(x2,x3). Ясно, что имеем:

f2(x1,x2,x3,x4)=g0(X0,g1(X1), g2(X1)),

где

g0(X0, s, t)=(x1&x4) s t, g1(X1)=x2 x3, g2(X1)=x2≡ x3.

В настоящее время получены критерии и для некоторых других видов как разделительной, так и неразделительной декомпозиций.