165
Алгоритм Дейкстры. begin
for каждой v V do begin
d[v]:= (А,v); PUTH(v):=A;
end
Отметить вершину А;
while остаются неотмеченные вершины do begin
u:=неотмеченную вершину с минимальным расстоянием от А;
Отметить вершину u;
for каждой неотмеченной вершины v с условием u,v Х do
begin
d*:= d[u]+ (u,v); if d*< d[v] then
begin
PUTH(v):= PUTH(u), v; end
end
end
end
Цепь не крепче своего самого слабого звена.
Английская пословица
§ 19. Потоки в сетях
Деятельность современного общества тесно связана с разного рода сетями – транспортные сети, электрические сети, сети нефтепроводов и т.д. Если различна пропускная способность элементов сети, то можно ставить вопрос о максимизации потоков в сетях. Например, есть сеть дорог, ведущих из Владивостока в Санкт-Петербург; известна пропускная способность каждой ветки; требуется определить максимальный поток грузов, допустимых для заключения договора о доставке контейнеров из Японии в Европу.
Сетью S (или транспортной сетью) называется орграф, обладающий следующими свойствами:
1)существует единственная вершина v0, называемая входом или источником, в которую не заходит ни одна дуга (полустепень захода вершины v0 равна нулю);
166
2)существует единственная вершина vk, называемая выходом или стоком, из которой не исходит никакая дуга (полустепень исхода вершины vk равна нулю);
3)каждой дуге х поставлено в соответствие неотрицательное действительное число ψ(х), называемое пропускной способностью
дуги.
Вершины в транспортной сети S, отличные от источника и стока,
называются промежуточными.
Потоком ϕ в сети называется действительнозначная функция ϕ, определенная на множестве дуг графа и удовлетворяющая следующим свойствам:
1)для любой дуги х, ϕ(х)≥ 0;
2)ϕ(х)≤ ψ(х) – поток по любой дуге х не превосходит ее пропускной способности;
3) для любой |
промежуточной вершины v выполняется |
равенство: ∑ ϕ( x ) − |
∑ϕ( x ) = 0 , где U v− ,U v+ - множество дуг графа, |
− |
+ |
x Uv |
x Uv |
соответственно заходящих в промежуточную вершину v и выходящих из нее. Это условие называется условием сохранения: в любой промежуточной вершине поток не создаётся и не исчезает.
Условие 3) можно сформулировать и следующим образом: сумма потоков по дугам, заходящим в произвольную промежуточную вершину сети, равна сумме потоков по дугам, исходящим из этой вершины.
Дуга называется насыщенной, если поток по ней равен её пропускной способности.
Притоком на выходе vk сети называется величина ϕv |
= |
∑ϕ( x ) . |
|
k |
− |
|
|
x Uv |
|
|
k |
Пусть A V - такое подмножество вершин сети, что v0 A, vk A. Разрезом сети U A− относительно множества вершин А называют
множество дуг, исходящих из вершин, не принадлежащих А, и заходящих в вершины А.
Пропускной способностью разреза U A− называют число ψ (U A− ) = ∑ψ (x) ,
x U A−
равное сумме пропускных способностей дуг разреза U A− .
Разрез с минимальной пропускной способностью называется
минимальным разрезом.
Поток в сети называется максимальным, если его величина принимает максимальное значение по сравнению с другими допустимыми потоками в данной сети.
Любой элемент, движущийся от v0 к vk, обязательно пройдет по какойлибо дуге разреза U A− , каков бы ни был этот разрез. Можно доказать следующую теорему.
167
Теорема 5.25. Для любой (транспортной) сети величина максимального потока равна наименьшей пропускной способности разрезов.
Эта теорема является подтверждением английской пословицы: «цепь не крепче своего самого слабого звена». Если хотя бы для одного разреза её пропускная способность мала, например равна р, то максимальный поток не больше р.
Алгоритм нахождения максимального (полного) потока в
(транспортной) сети. Пусть имеем (транспортную) сеть S и пусть поток ϕ в сети и пропускные способности дуг принимают целочисленные значения. Для нахождения максимального потока в сети S выполняем следующие действия.
Шаг 1. Полагаем, что начальный поток ϕ равен нулю, т. е. для любой дуги х сети ϕ(х)=0. Полагаем S*= S.
Шаг 2. Удаляем из орграфа S* все дуги, являющиеся насыщенными при потоке ϕ в сети S*. Полученный орграф вновь обозначим через S*.
Шаг 3. Ищем в S* простой путь Z(v0,vk) из v0 в vk . Если такого пути нет, то ϕ - искомый поток в сети S. Иначе идем к следующему шагу.
Шаг 4. Увеличиваем поток ϕ(х) на каждой дуге х из Z(v0,vk) на одинаковую величину а, a>0, такую, что, по крайней мере, одна дуга из Z(v0,vk) оказывается насыщенной, а потоки по остальным дугам из Z(v0,vk) не превышают их пропускных способностей. При этом величина потока ϕ также увеличивается на а и поток ϕ остается в S допустимым. После этого переходим к шагу 2.
§20. Вопросы и темы для самопроверки
1.Основные типы графов.
2.Различные способы задания графа.
3.Изоморфизм графов.
4.Число ребер графа.
5.Цепи и простые цепи.
6.Связные компоненты.
7.Матрица смежности графа и орграфа.
8.Можно ли определить локальные степени вершин графа по её матрице смежности?
9.Операции над матрицами смежности.
10.Матрицы смежности и достижимости графа и орграфа.
11.Критерии изоморфизма графов.
12.Матрица инциденций графа и орграфа.
168
13.Что можно определить по матрице инциденций графа?
14.Деревья.
15.Основные свойства деревьев.
16.Ориентированные деревья.
17.Задача о минимальном соединении.
18.Эйлеровы графы.
19.Критерий эйлеровости графа.
20.Алгоритм построения эйлерова цикла.
21.Гамильтоновы графы.
22.Планарные графы. Непланарность графов К5 и К3,3.
23.Критерий планарности графов.
24.Задачи о кратчайшей цепи в графе с ребрами единичной длины.
25.Задача о кратчайшей цепи в графе с ребрами произвольной длины.
26.Алгоритм Дейкстры нахождения кратчайших путей в орграфе.
27.Потоки в сетях.
28.Нахождение максимального потока.
Упорство – благоприятно.
И. Цзин
§21. Упражнения
1.Построить всевозможные неизоморфные непомеченные графы с тремя вершинами.
2.Построить всевозможные неизоморфные непомеченные орграфы с тремя вершинами. Сколько их и сколько среди них направленных графов?
3.Построить всевозможные неизоморфные графы с тремя помеченными вершинами.
4.Построить всевозможные неизоморфные орграфы с тремя помеченными вершинами.
5.Определить максимально возможное число ребер в графе с n вершинами.
6.Дан граф с 2n (n ≥ 2) вершинами, перенумерованными числами 1, 2, …, 2n. Смежными являются только вершины с нечетными номерами, и только они. Сколько ребер в этом графе?
7.Пусть граф состоит из вершин и ребер тетраэдра. Определите локальные степени его вершин. Является ли граф полным?
8.Пусть граф состоит из вершин и ребер куба. Сколько ребер нужно добавить, чтобы получить полный граф?
9.Построить полный граф с 5 вершинами; с 7 вершинами.
10.Пусть дан граф G = (V, X), представленный на рис.5.17. Задать его:
1)перечислением множества вершин и множества ребер;
2)перечислением списков смежностей.
169
11.Пусть граф состоит из вершин и ребер четырехмерного куба. Сколько вершин и сколько ребер имеет этот граф?
12.Используя принцип Дирихле, докажите, что если граф G имеет более одной вершины, то у него найдутся, по крайней мере, две вершины одинаковой степени.
13.Изоморфны ли графы, представленные на следующем рисунке?
14.Изоморфны ли графы, представленные на следующем рисунке?
15.Изоморфны ли графы, представленные на следующем рисунке?
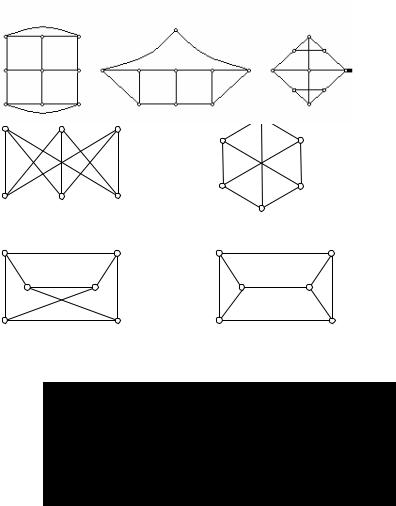
16.На следующем рисунке даны графы, представленные своими диаграммами. Определите, изоморфны ли эти графы.
17.Постройте однородный (регулярный) граф степени 3 с 4 вершинами; с 6 вершинами; с 8 вершинами. Можно ли построить однородный граф степени 3 с 5 вершинами?
18.Пусть дан граф G, представленный на рис. 5.29. Постройте для G:
а) матрицу смежности; б) матрицу инцидентности.
19. Логическая матрица смежности орграфа G имеет вид:
|
Л |
И |
|
|
|
|
|
М = |
Л |
Л |
|
|
Л |
Л |
|
|
|
||
|
|
|
|
|
И |
Л |
|
Вычислите М 2, М 3 и М 4.
ЛЛ
И |
Л |
||
Л |
И |
. |
|
|
|||
|
|
||
Л |
Л |
||
Найдите матрицу достижимости М*.
170
20. Дана матрица АG смежности графа G. Постройте диаграмму графа
G. |
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
1 |
||
АG = 1 |
1 |
0 1 |
0 |
|||
|
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
||
21. Дана матрица инцидентности IM графа. Постройте диаграмму графа.
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
||
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
IM = |
0 0 1 0 0 0 0 |
|
||||||
0 |
0 |
0 |
1 |
0 |
0 |
1 |
||
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|||||||
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
||
22.Задайте различными способами определённые далее графы:
а) G1 имеет вершинами вершины тетраэдра, а рёбрами – рёбра тетраэдра;
б) G2 имеет вершинами вершины тетраэдра, а рёбрами являются рёбра тетраэдра и петли во всех вершинах тетраэдра;
в) G3 имеет вершинами вершины куба, а рёбрами – рёбра куба; г) G4 имеет вершинами вершины октаэдра, а рёбрами – рёбра октаэдра;
23.Постройте матрицы инциденций и смежности полного графа с пятью вершинами.
24.Постройте матрицы инциденций и смежности графа, состоящего из вершин и ребер куба.
25.Постройте полный двудольный граф: а) К2,3 ; б) К3, 4.
26.Постройте полный двудольный граф К4,4. Если удалить одну из вершин графа, то сколько ребер остается в полученном графе?
27.Сколько ребер имеет полный двудольный граф Кm,n?
28.Какое минимальное число ребер нужно удалить из графа Кm,n, чтобы получить граф с одной изолированной вершиной?
29.Покажите, что связный граф с n вершинами содержит не менее n – 1
ребер.
30.Каково минимальное число ребер в остовном связном подграфе графа с n вершинами?
31.При каких числах n и m в графе Кm,n существует гамильтонов цикл?
171
32.При каких числах n и m в графе Кm,n существует эйлеров цикл?
33.Пусть граф состоит из вершин и ребер тетраэдра. Будет ли он планарным?
34.Пусть граф состоит из вершин и ребер куба. Будет ли он планарным?
35.Является ли планарным граф К2,2; граф К2,3; граф К3,3; граф К3,4?
36.Является ли планарным граф К4; граф К5; граф К6?
37.Постройте все неизоморфные деревья: с 4 вершинами; 5 вершинами; 6 вершинами.
38.Постройте все неизоморфные ордеревья: с 3 вершинами; 4 вершинами.
39.Сколько ребер нужно отбросить в графе Кn,m, чтобы получить остовное дерево?
40.В графе К3,5 введите длины ребер так, чтобы любые два ребра имели различные длины. Постройте остовное дерево, сумма длин ребер которого наименьшая из возможных.
41.Требуется оповестить всех членов садоводческого общества о собрании. Пусть на один телефонный звонок требуется одна минута. Положим, что каждый оповещённый сразу последовательно звонит двум ещё не оповещённым членам садоводческого общества. Положим также, что все телефоны в нужный момент свободны и работают, а члены рассматриваемого общества оказываются у телефонов.
В начальный момент председатель общества звонит двум членам общества (последовательно сначала одному, затем другому, тратя по одной минуте). Каждый, получивший известие, поступает также, как и председатель, оповещая двух неоповещённых.
Сколько времени потребуется, чтобы оповестить: а) 600 человек? б) 3000000 (три миллиона) человек?
Сколько новых человек будут узнавать о собрании на k-й минуте после начала оповещения?
Указание: построить дерево оповещения, обращая внимание на уровни дерева и на то, что рёбра дерева имеют различную длину.
42.Члены клуба «Арстран» проводят регулярные встречи через равные промежутки времени. Каждый человек, вступающий в клуб «Арстран», должен внести взнос в сумме 26 400 рублей. После этого он получает статус партнёра 1-й степени и имеет право приглашать на встречи по одному гостю
–будущему партнёру клуба. Если А – партнёр 1-й степени лично вовлёк в клуб партнёров А1, А2, А3, А4,…, АN, N >2, (т.е. более двух новых партнёров), то он считается партнёром 2-й степени для членов А3, А4,…,АN. Для А1 и А2 он (партнёр А) является партнёром 1-й степени. Если А1 или А2 вовлёк в клуб партнёра С, то А является партнёром 2-й степени для С.
Распределение взносов в клубе осуществляется следующим образом. Если В приглашен партнёром 1-й степени, то взнос партнёра В
распределяется:
- 4 000 рублей получает В1 – его пригласитель (партнёр 1-й степени);
172
-8 000 рублей получает В2 – партнёр 2-й степени (для В), который лично приглашал партнёра В1;
-2 400 рублей получает консультант клуба;
-12 000 рублей поступают руководителям клуба.
Если В приглашен партнёром В2 2-й степени, который лично пригласил более двух новых членов, и В является более, чем вторым из приглашенных партнёром В2, то взнос партнёра В распределяется:
-12 000 рублей получает – его пригласитель В2 (партнёр 2-й степени);
-2 400 рублей получает консультант клуба;
-12 000 рублей поступают руководителям клуба.
Положим, что каждый член клуба желает компенсировать свой взнос, приглашая в клуб новых участников. Будем считать, что каждый член клуба приглашает на ближайшие встречи только двух человек (по одному на встречу по правилам клуба).
1.Пусть в городе проживает 489 395 взрослых, каждый из которых может (и согласен) заплатить по 26 400 рублей, и их вовлекли в члены клуба. Сколько среди них окажется людей, которые не смогут компенсировать свои взносы?
2.На какой по счёту встрече, при работе по принятой схеме (каждый приглашает двух на ближайшие встречи), вступившими в клуб окажутся: а) 1104 человека; б) 900140 человек (если есть столько возможных членов)?
3.Какое минимальное число новых членов надо вовлечь в клуб отдельному члену клуба, чтобы компенсировать свой взнос?
Указания: использовать схему решения предыдущей задачи.
Ответы для задачи 42: 1) 410744 (т.е. 83,93 % партнёров не смогут компенсировать свой взносы); 2а) - 12; 2б) - 23; 3) 2 (исходя из минимальности усилий других участников).