13
1)( A ) =A – свойство инволютивности;
2)A B=B A
3)A∩B=B∩A
4)A (B C)=(A B) C
5)A∩(B∩C)=(A∩B)∩C
6)A∩(B C)=(A∩B) (A∩C)
7)A (B∩C)=(A B)∩(A C)
8)A∩(А В)=A
9)A (А∩В)=A
10)A =A
11)A U = U
12)A∩=
13)A∩ U =A
14)A B= A ∩B
15)A∩B= A B
16)A A= U
17)A ∩A=
18)A A=A
19)A∩A=A
- законы ассоциативности;
– законы дистрибутивности;
и с U;
Докажем, например, равенство 1). Пусть х ( A ) . Имеем, что х ( A ) тогда и только тогда, когда х A . Последнее имеет место тогда и только
тогда, когда х А. Итак, ( A ) =А. Аналогичным образом можно доказать и остальные соотношения 2) - 19).
|
§ 3. Разбиение множества. Декартово произведение |
|
|
Семейство подмножеств {B1, B2, …, Bn}, образует |
B1 |
B2 |
|
разбиение множества А тогда и только тогда, когда |
|
|
|
1) |
Bi≠, 1≤ i≤ n; |
B3 |
|
2) |
Bi∩Bj = если i≠j; |
B4 |
|
3) |
B1 B2 … Bn=A. |
|
|
|
|
||
Пример разбиения приведен на рис. 1.6. |
Рис. 1.6 |
|
|
Пусть А и В – два множества и положим а А, b B, |
|
||
с А, d B. |
|
|
|
Упорядоченной парой называется объект a,b такой, что a,b = c,d тогда и только тогда, когда а=с и b=d. В упорядоченной паре a,b элемент а считается первым элементом, b – вторым.
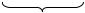
14
Декартовым (прямым) произведением двух множеств А и В называется множество упорядоченных пар a,b , таких, что а А и b B. Декартово (прямое) произведение обозначается через А×В. Итак:
А×В={ a,b : а А и b B}.
Пусть А={0,1}, B={a,b}, тогда А×В={ 0,a , 1,a , 0,b , 1,b }. Упорядоченной n-кой элементов a1, a2,…, an, a1 A1, a2 A2,…,an An,
называется объект a1,a2,…,an , такой что a1,a2,…,an = b1,b2,…,bn , b1 A1,
b2 A2,…,bn An, тогда и только тогда, когда a1=b1, a2=b2, …, an=bn.
Декартовым произведением множеств A1,А2,…,Аn называется множество упорядоченных n-ок:
A1× A2×…×An={ a1, a2, …,an : a1 A1 и a2 A2 и … и an An}.
Введём обозначение: An=A×A×…×A. n-раз
Можно доказать, что, например, выполняются следующие равенства:
(A B)×C =(A×C) (B×C);
(A∩B)×C =(A×C)∩ (B×C); (A\B)×C =(A×C)\(B×C) и т.п.
§ 4. Отношения
Бинарным отношением на (двух) множествах А и В называется подмножество R декартового произведения А×В.
Таким образом, если задано подмножество R множества А×В, т.е. некоторое подмножество упорядоченных пар a,b таких, что a A, b B, то говорим, что задано бинарное (двуместное) отношение R, и пишем
a,b R или aRb.
Последнее читается: элемент а находится в отношении R с b. Следовательно, изучение отношений сводится к изучению подмножеств множества A×B.
Отношение на множествах А и А, т.е. подмножество множества А×А
называется бинарным отношением на множестве А.
Рассмотрим пример. Пусть A=(-∞,∞). Рассмотрим А×А, т.е. плоскость и выберем: R1 – биссектрису первого квадранта,
R2 – полуплоскость выше R1,
R3 – полуплоскость ниже R1,
см. Рис. 1.7.
Очевидно, что R1, R2 и R3 есть следующие отношения: R1 – отношение равенства: y=x; R2 – отношение неравенства: y>x; R3 – отношение неравенства: y<x.
|
15 |
|
R1 |
R2 |
R3 |
|
Рис. 1.7 |
|
Областью определения бинарного отношения R называется множество |
||
DR={x А: существует такое y B, что xRy}. |
|
|
Областью значений бинарного отношения R называется множество |
||
ImR={y B: существует такое x A, что xRy}. |
|
|
Легко видеть, что область значений отношения R (R А В) совпадает с |
||
проекцией R на множество В, которое вводится как |
|
|
prBR={y B: существует такое x A, что x,y R}, |
|
|
т.е. prBR = ImR, а область значений R совпадает с проекцией R на A |
||
DR=prAR={x A: существует такое у В, что x,y R}, см. рис. 1.8. |
||
|
B |
|
|
R |
|
ImR=prBR |
|
|
JmR=prBR |
|
|
|
|
A |
|
DR=prBR |
|
|
DR=prAR |
|
|
Рис. 1.8 |
|
16
Образом элемента х А при отношении R называется множество ImR(x) элементов y B таких, что xRy, т.е.
ImR(x)={y B: x,y R}.
Прообразом элемента y B при отношении R называется множество kerR(y) элементов x A таких, что xRy, т.е.
kerR(y)={x A: x,y R}.
Единичным отношением Е (или I) называется бинарное отношение на множестве А такое, что
Е={ a,a : a A}.
Пустое отношение определяется пустым подмножеством множества
А В.
Универсальное отношение U на множествах А и В совпадает с А В:
U={ a,b : a A и b B}.
Способы задания отношения R:
1)перечислением упорядоченных пар x,y , принадлежащих R;
2)предикатом P: R={ x,y : P(x,y)};
3)порождающей процедурой: R={ x,y : x=f, y=ϕ};
4)бинарное отношение R на конечном множестве А можно задать
матрицей отношения. Пусть имеем множество A={a1, a2, …, an}, тогда матрица отношения R есть n n матрица MR =(mij) такая, что
1, если ąi ,a j R, mij = 0, если ąi ,a j R.
5)отношение R на конечных множествах А и В тоже можно задать n m
матрицей отношения MR =(mij), здесь n и m числа элементов в множествах А и В соответственно и
1, если ąi ,b j R, ai A, b j B, mij = 0, если ąi ,b j R, ai A, b j B.
6) отношение R на конечных множествах А и В можно задать n m (логической) матрицей отношения вида LR =(lij), здесь n и m числа элементов в множествах А и В соответственно и
И, |
если аi ,b j R, ai |
A, b j |
B, |
|
lij = |
Л, |
если аi ,b j R, ai |
A, b j |
B. |
|
||||
7)бинарное отношение R на конечном множестве А можно задать
графом. Пусть A={a1, a2, …, an}, тогда элементы ai (1≤ i ≤ n) рассматриваются как вершины графа. Если ai,аj R, то из вершины ai идёт дуга в вершину aj, иначе – из ai нет дуги в aj. В результате получим орграф, представляющий отношение R. Ясно, что бинарное отношение R на конечных множествах А и В тоже можно задать графом, выбирая в качестве вершин элементы из А В. При этом