149

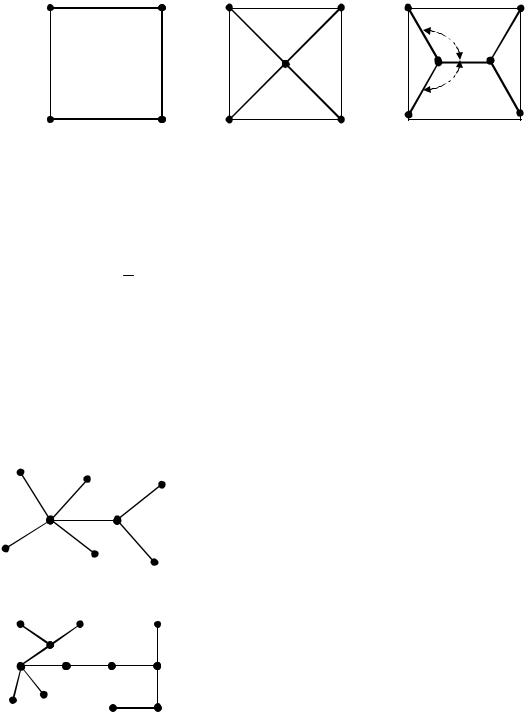
Поясним это на примере. Пусть задано, что четыре города расположены в вершинах квадрата с единичной стороной. В случае, если этот граф имеет ребрами только стороны квадрата, то остовное дерево с минимальной мерой представлено на рис. 5.22, а) и его мера (Т) = 3.

v1

v2

v1

v2

v3	v4	v3	v4
	а)		б)

v1	v2
	1200
	1200
v3	v4
	в)

Рис. 5.22

Введем новую вершину на пересечении диагоналей квадрата. Тогда остовное дерево с минимальной мерой представлено на рис. 5.22, б) и его мера (Т) =2 2 =2,828. Если ввести две новые вершины (точки разветвления), то оптимальное остовное дерево, представленное на рис. 5.22, в), имеет меру (Т) =2,732. Таким образом, нужно четко представлять цель исследования.

Нельзя судить о дереве по его коре.

Английская пословица

v

u

а)

v u

б)

Рис. 5.23

§ 12. Центры дерева

Пусть каждое ребро графа G имеет единичную длину. Длина цепи, соединяющей вершины v и u, в этом случае, равна числу ребер этой цепи. Пусть v – некоторая вершина дерева G, от которой можно прийти к любой другой вершине u, при этом длину цепи обозначим через d(v,u). Максимальное из этих величин d(v,u) по всевозможным u G называется

эксцентриситетом вершины v и обозначается как

е(v). Итак, эксцентриситет вершины v равен числу

е(v) = max d(v,u). На рис. 5.23, а) приведён граф

u G

(дерево), для вершин v и u которого, очевидно,

имеем: е(v) = 3, е(u) = 2.

Наибольший из эксцентриситетов вершин

150

графа G называется диаметром графа G, который обозначают d(G), d(G)=

max d(v,u). Таким образом, диаметр графа G равен длине наибольшей

v ,u G

простой цепи графа.

Радиусом r(G) называется наименьший из эксцентриситетов вершин

графа G: r(G) = = min e(u).

u G

Вершина v называется центральной вершиной графа G, если e(v)= r(G). Центр графа G – это множество всех центральных вершин. На рис. 5.23, б) построен граф, для которого d(G)=7, r(G)=4, а центр состоит из двух вершин v и u.

Теорема 5.14. Каждое дерево имеет центр, состоящий или из одной вершины, или из двух смежных вершин.

Доказательство. Утверждение очевидно для 1 и 2-х вершинных графов. Покажем, что у любого дерева Т те же центральные вершины, что и у дерева Т’, полученного из Т удалением всех его висячих вершин.

Ясно, что расстояние от данной вершины v любого дерева Т до любой другой вершины u может достигать наибольшего значения только тогда, когда u – висячая вершина.

Таким образом, эксцентриситет каждой оставшейся в Т’ вершине точно на единицу меньше эксцентриситета этой же вершины в Т. Отсюда следует, что вершины дерева Т, имеющие наименьший эксцентриситет в Т, совпадают с вершинами, имеющими наименьший эксцентриситет в Т’, т.е. центры деревьев Т и Т’ совпадают. Если процесс удаления висячих вершин продолжить, то получим последовательность деревьев с тем же центром, что и у дерева Т. В силу конечности Т обязательно придем к 1 или 2-х вершинному дереву. В любом случае все вершины дерева, полученного таким образом, образуют центры дерева Т, и этот центр состоит или из единственной вершины, или из двух смежных вершин.

Зри в корень.

К. Прутков

§ 13. Ориентированные деревья

Ориентированным деревом (или ордеревом, или корневым деревом)

называется орграф со следующими свойствами:

1)существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ордерева;

2)полустепень захода всех остальных вершин равна 1;

3)каждая вершина достижима из корня.

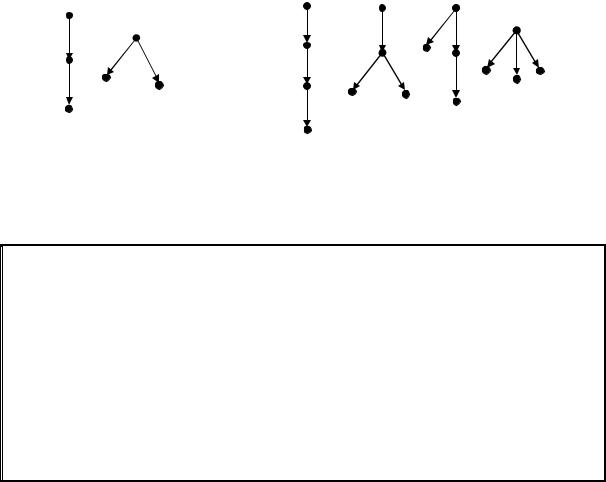
На рис. 5.24 приведены всевозможные ордеревья с тремя (рис 5.24, а) и с четырьмя (рис 5.24, б) вершинами.

151

а)

б)

Рис. 5.24

Пусть, как обычно, n – число вершин, а m – число дуг орграфа.

Теорема 5.15. Ордерево обладает следующими свойствами:

1)m = n – 1;

2)если в ордереве отменить ориентацию ребер, то получится дерево;

3)в ордереве нет контуров;

4)для каждой вершины существует единственный путь, ведущий в эту вершину из корня;

5)подграф, определяемый множеством вершин, достижимых из некоторой вершины v данного ордерева, является ордеревом с корнем v (это ордерево называется поддеревом вершины v);

6)если в свободном дереве любую вершину назначить корнем и ввести ориентацию ребер от корня к концевым вершинам, то получится ордерево.

Доказательство:

1.Каждая вершина достижима из корня и полустепени захода всех вершин кроме корневой вершины, равны единице, следовательно, m = n -1.

2.Пусть G – ордерево, граф G′ получен из G отменой ориентации

ребер, u – корень. Тогда для v1,v2 V существуют цепи Z(v1,u) и Z(u,v2) в графе G′, поэтому любые две вершины v1,v2 V соединены цепью Z(v1,v2)= Z(v1,u) Z(u,v2), следовательно, граф G ′ связен. Допустим, что G ′ содержит цикл С и v1,v2 различные вершины этого цикла. Тогда, кроме цепи Z(v1,v2)=

Z(v1,u) Z(u,v2), должна быть другая цепь Z*(v1,v2), соединяющая вершины v1 и v2. Следовательно, в графе G одна из вершин v1 или v2 должна иметь полустепень захода больше чем единица, что не может быть. Таким образом, допущение неверно и G ′ не имеет циклов, т.е. G′ - дерево.

3.Следует из 2.

4.От противного. Если бы в G существовали два пути из u в v, то в

G′ имелся бы цикл.

Утверждения 5) и 6) теоремы 5.15 оставляем читателю в качестве упражнений.

Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой

152

ветви. Уровень вершины ордерева – это расстояние от корня до выбранной вершины (если считаем, что все дуги имеют единичную длину). Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.

Для деревьев применяется ещё и «генеалогическая» терминология. Вершина v, достижимая из вершины u, называется потомком вершины u; вершина u называется предком для v. Если u и v - смежные вершины, то u

называют отцом (родителем) для v, а v - сыном (дитём) для u. Ясно, что лист не имеет потомков.

Как правило, при изображении дерева и ордерева корень располагают наверху и его ветви идут вниз, что естественно при использовании генеалогической интерпретации. Поэтому иногда при изображении ордерева не указывается ориентация ребер, ибо она всегда направлена от корня.

Ориентированное дерево называют бинарным, если полустепень исхода любой его вершины не больше двух.

Бинарное ориентированное дерево называют полным, если из любой его вершины, не являющейся листом, исходят ровно две дуги, а ярусы (уровни) всех листьев совпадают. Можно доказать, что в полном ориентированном дереве высоты h имеется ровно 2h листьев.

Всякое (свободное) дерево можно ориентировать, назначив одну из вершин (любую вершину) корнем.

	Где начало того конца, которым
	оканчивается начало?
	К. Прутков
	§ 14. Эйлеровы графы
	Рассмотрим упоминавшуюся в начале этой
А	главы задачу о кенигсбергских мостах. В
	Кёнигсберге (ныне Калининград) было два острова,
	соединенных семью мостами с берегами реки
С	D Преголя и друг с другом, как показано на рис. 5.1.
	Каждый мост имел свои названия: Лавочный,
	Зелёный, Пороховой, Кузнечный, Деревянный,
	Высокий и Медовый. Нужно выяснить, существует
В	ли маршрут прогулки, проходящий через каждый
	мост один и только один раз, и такой, что позволял

Рис. 5.25

бы, выйдя из произвольной точки города, вновь вернуться в эту же точку.

Части города, лежащие на северной и южной сторонах реки, обозначим соответственно через А и В. Западный остров обозначим через С, а восточный – через D. Так как нас интересуют только переходы по мостам, можно считать A, B, C и D вершинами некоторого графа, ребра которого отвечают соответствующим мостам. В результате получим граф, диаграмма

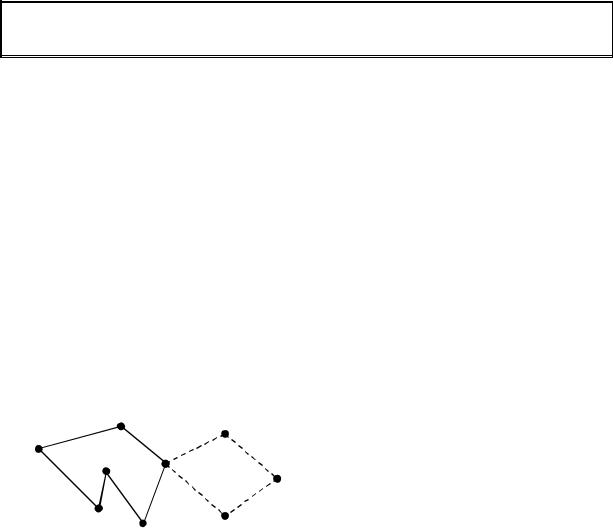
153

которого изображена на рис. 5.25. Эйлер показал, что этот граф не представляет единого цикла. Ибо если бы он существовал, то в каждой вершине графа было бы столько же входящих в нее ребер, сколько и выходящих из нее, т.е. в каждой вершине графа было бы четное число ребер.

Таким образом, из какой бы вершины не начинался обход, обойти весь граф и вернуться обратно невозможно, не проходя никакого ребра дважды.

Изложив решение задачи о кенигсбергских мостах, Эйлер в своей работе перешел к следующей общей проблеме теории графов: на каких графах можно найти цикл С, содержащий все ребра графа, причем каждое ребро в точности по одному разу? Такой цикл, т.е. цикл, содержащий все ребра графа в точности по одному разу, называется эйлеровым циклом, а граф, обладающий эйлеровым циклом – эйлеровым графом.

Теорема 5.17. Конечный граф G является эйлеровым графом тогда и только тогда, когда: 1) G связен; 2) все его локальные степени четны.

Доказательство. Необходимость условия 1) очевидна. Далее, каждый раз, когда эйлеров цикл проходит через какую-то вершину, он должен войти в нее по одному ребру и выйти по другому, поэтому условие 2) также необходимо.

Достаточность. Пусть условие 1) и 2) выполняется. Докажем, что граф эйлеров. Начнем цепь С в произвольной вершине v графа G и будем продолжать ее, насколько возможно, все время через новые ребра. Так как в каждой вершине число ребер четно, этот процесс может закончиться только в v, следовательно, цепь С будет циклом. Если C проходит через все ребра графа G, то цикл построен. Если же C содержит не все ребра графа G, то удалим из G ребра этого цикла С, в результате получим подграф G*. Графы С и G имеют четные локальные степени, следовательно, то же должно быть справедливо и для G*. Так как граф G связный, в C должна существовать вершина u, инцидентная ребрам из G*, см. рис. 5.26. Из вершины u можно построить новую цепь С*, содержащую ребра только из G*, и такая цепь может закончиться только при возвращении в u. Пусть S(v,u) и S(v,u) две

	цепи, из которых образован цикл С.
v	Тогда можно составить новый цикл:
u					который
	С1=S(v,u)	С*		S(v,u),
	возвращается в v и содержит больше
	ребер, чем С, см. рис. 5.26, где цикл С
	изображен сплошной линией, а цикл
	С* – штриховой. Если С1 не является
Рис. 5.26	эйлеровым циклом, то это построение
	повторяется.			Когда	процесс

закончится, эйлеров цикл будет построен. Теорема доказана.

154

Доказательство теоремы даёт и алгоритм нахождения эйлерового цикла. Для нахождения эйлерового цикла можно построить алгоритм в следующем виде:

Алгоритм построения эйлерового цикла:

Вход: эйлеров граф G(V,X), заданный списками смежности (L[v] – список вершин, смежных с вершиной v).

Выход: последовательность вершин эйлерова цикла. S:= {стек для хранения вершин}

select v V {произвольная вершина} v → S {положить v в стек S}

while S≠ do

v ← S; v → S {v - верхний элемент стека} if L[v] = then

v ← S; yield v else

select u L[v] {взять первую вершину из списка смежности} u → S {положить u в стек}

L[v]:= L[v]\ {u}; L[u]:= L[u]\{v} {удалить ребро v,u } end if

end while

Можно поставить аналогичную задачу для отыскания цепи, начинающейся в некоторой вершине v и заканчивающейся в другой вершине u, причем содержащей каждое ребро один и только один раз.

Теорема 5.18. Для того чтобы на связном графе имелась цепь S(v,u), содержащая все его ребра в точности по одному разу, необходимо и достаточно, чтобы v и u были единственными вершинами нечетной степени для этого графа.

Доказательство. Необходимость. Пусть имеется цепь S(v,u), проходящая по всем ребрам в точности по одному разу. Эта цепь начинается в вершине v, возможно, в дальнейшем снова заходит в v, и далее не один раз. Если цепь не заканчивается в v, то эта вершина должна иметь нечетную степень. Аналогично и для u, в то время как все остальные вершины графа должны быть четны.

Достаточность. Пусть v и u - единственные вершины с нечётной степенью. Добавим к графу G ребро (v,u), тогда все вершины будут иметь четную степень и согласно теореме 5.17 граф обладает эйлеровым циклом; если из этого цикла удалить ребро (v,u), останется искомая цепь S(v,u). Что и требовалось доказать.