5. Основные теоремы теории вероятности

1. Теоремы сложения вероятности

Пусть А, В – случайные события.

Определение:

Под суммой двух событий (А+В) понимается такое событие, которое имеет место произошло хотя бы одно из событий А или В (либо происходит А, либо происходит В, либо они происходят одновременно). Пример 1 (суммы двух событий).

Стреляем по мишени из двух орудий.

Пусть А – попали в мишень при стрельбе из 1^го орудия.

В – попали в мишень из 2^го орудия.

Тогда А+В – либо мы попали из 1^го орудия, либо попали из 2^го орудия, либо попали одновременно. Замечание. Если А и В – это несовместные события, то А+В – либо произошло А, либо произошло В. Не попадание – это будет противоположное событие к сумме.

Теорема 1 (теорема сложения вероятностей для несовместных событий).

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Р(А+В)=Р(А)+Р(В).

{ Пусть n – общее число всех возможных исходов, m – число элементарных исходов, благоприятствующих наступлению события А, k – число исходов, благоприятствующих наступлению события В. Тогда m+k – число исходов, благоприятствующих наступлению А+В. Используя определение классической вероятности, получаем:

Р(А+В) ==+= Р(А)+Р(В) }

Следствие. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий А₁, А₂, …А_n

P=

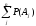
Пример 2. В урне находятся три белых шара, пять красных, два синих. Какова вероятность того, что шар, извлеченный из урны, не белый?

Обозначим:

{ А – шар не белый

В – шар, извлеченный из урны, красный

С – шар, извлеченный из урны, синий

Число всех исходов n=10, т.к. шаров всего 10.

Число благоприятствующих исходов для В равно 5.

Число благоприятствующих исходов для С равно 2, т.е.

P(B)==;P(C)==

Событие А=В+С, т.к. В и С – несовместны, следовательно, применим теорему 1.

Р(А) =Р(В)+Р(С)=+=}

Определение:

Произведением двух случайных событий А и В называется (А·В) событие, состоящее в том, что события А и В наступают одновременно.

Пример 3. А – деталь стандартная.

В – деталь окрашенная.

А·В – деталь стандартная и окрашенная.

Теорема 2 (теорема сложения для двух совместных событий)

Если события А и В совместные, то вероятность суммы этих двух событий равна сумме вероятностей этих событий без вероятности наступления произведения этих событий.

Р(А+В)=Р(А)+Р(В)-Р(А·В)

{ Рассмотрим все исходы, в которых появляются события А и В.

Возможны следующие события:

1. А·В (А наступило, В – не произошло)

2. Ā·В (В – происходит, А – не произошло)

3. А·В

Все эти три события уже несовместны, т.е. одновременно наступить не могут. Тогда

А+В=А·В+Ā·В+А·В

Так как события несовместны, то по теореме 1

Р(А+В)=Р(А·В)+Р(Ā·В)+Р(А·В) (*)

Так как Ā·В и А·В – несовместны, то событие В наступит, если имеет место либо Ā·В, либо А·В, поэтому В=Ā·В+А·В.

По теореме 1, Р(В)=Р(Ā·В)+Р(А·В), отсюда Р(Ā·В)=Р(В)-Р(А·В).

Аналогично, т.к. А·В и А·В – несовместны и А=А·В+А·В и по теореме 1 Р(А)=Р(А·В)+Р(А·В), значит

Р(А·В)=Р(А)-Р(А·В).

Подставим получившееся равенство в (*).

Р(А+В)=Р(А)-Р(А·В)+Р(В)-Р(А·В)+Р(А·В), т.е.

Р(А+В)=Р(А)-Р(А·В)+Р(В)

Теорема доказана. }

Пример 4. Найти вероятность того, что при подбрасывании игральной кости выпадает четное или кратное 3 число очков.

{ Обозначим

А – выпадение четного числа очков

В – число очков, кратных 3

Всего исходов 6. Наступлению событию А благоприятствует три исхода (выпадение 2, 4 либо 6). Наступлению событию В благоприятствует два исхода (выпадение 3 или 6).

Т.к. события А и В – являются совместными, то

Р(А+В)=Р(А)+Р(В)-Р(А·В)

Вычислим Р(А), Р(В), Р(А·В)

Р(А) ==

Р(B) ==

Р(А·В ) ==,поэтому

Р(А+В ) =+-==}

Теорема 3. Вероятность суммы полной системы событий равна 1.

{ Пусть А₁, А₂, …А_n – полная группа событий, тогда событие А₁+ А₂+…+ А_n - является достоверным событием.

По свойству вероятности имеем

Р(А₁+ А₂+…+ А_n)=1, поскольку

А₁, А₂, …А_n полная группа событий, то

Р(А₁+ А₂+…+ А_n)= Р(А₁)+Р(А₂)+…+Р(А_n), поэтому

Р(А₁)+Р(А₂)+…+Р(А_n)=1 }

2. Теорема умножения вероятностей

Определение:

Событие А называется независимым от события В, если вероятность события А не изменится от того, произошло событие В или нет. В противном случае, событие А называется зависимым от события В.

Определение:

Вероятность события А, вычисленная в предположении, что событие В произошло, называют условной вероятностью события А и обозначают Р(А\В), либо Р_В(А).

Пример 5. Бросают две игральные кости. Сумма выпавших очков равна 6. Вычислить вероятность того, что одна из цифр этих очков равна 2.

{ Будем обозначать через (а, в) возможные исходы из числа всех исходов, а – количество очков, выпавших на первой игральной кости, в – количество очков, выпавших на второй игральной кости.

Тогда возможные исходы:

(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)

А – сумма цифр, равная 6