
- •Глава 8. Исследование поведения функций
- •§ 8.1. Исследование поведения функций одной переменной
- •8.1.1. Условия монотонности функции
- •8.1.2. Локальные экстремумы функции
- •8.1.3. Наибольшее и наименьшее значение функции на отрезке
- •8.1.4. Выпуклость функции
- •8.1.5. Асимптоты графика функции
- •§ 8.2. Экстремумы функций нескольких переменных
- •8.2.1. Необходимое условие экстремума
- •8.2.2. Достаточное условие экстремума функции
- •§ 8.3. Глобальные экстремумы функции
- •8.3.1. Понятие глобального экстремума функции
- •8.3.2. Необходимое условие глобального экстремума
- •8.3.3. Метод Лагранжа отыскания
8.1.3. Наибольшее и наименьшее значение функции на отрезке
Если функция
непрерывна на отрезке
![]() ,
то из второй теоремы Вейерштрасса
следует, что среди точек отрезка
,
то из второй теоремы Вейерштрасса
следует, что среди точек отрезка![]() найдется точка, в которой
найдется точка, в которой
функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение. Если эти точки не совпадают с концами отрезка, то они являются точками локального экстремума и, значит, критическими точками функции (при условии, что функция имеет производную).
Если функция
![]() имеет на отрезке
имеет на отрезке![]() конечное число критических точек
конечное число критических точек![]() ,
то наибольшее
,
то наибольшее![]() и
наименьшее
и
наименьшее![]() значение функции
значение функции![]() на
на
отрезке
![]() находятся по формулам
находятся по формулам
![]() ,
,
![]() .
.
Примеры
6. Найти наибольшее
и наименьшее значение функции
![]() на отрезке
на отрезке![]() :
:![]() ,
,![]() .
.
Решение.
Функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() и имеет производную в каждой точке этого
отрезка, кроме точки
и имеет производную в каждой точке этого
отрезка, кроме точки![]() :
:
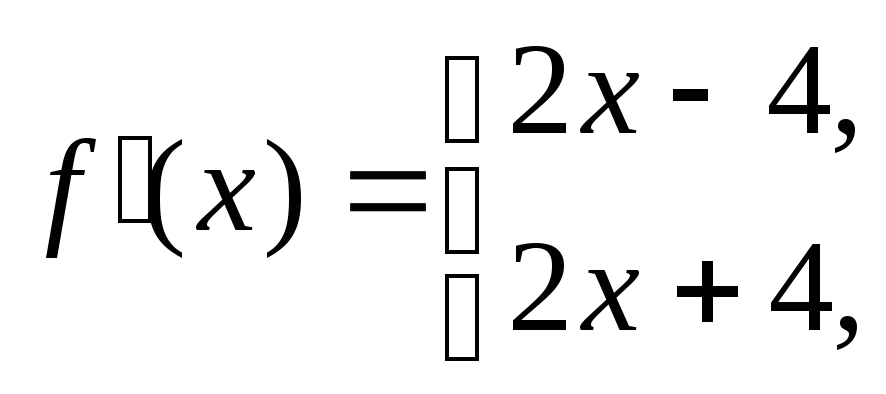
![]()
![]()
В точках
![]() и
и![]() производная функции
производная функции![]() равна нулю. Вычислим
равна нулю. Вычислим
значения
![]() в критических точках
в критических точках![]() ,
,![]() ,
,![]() и на концах отрезка
и на концах отрезка![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Отсюда следует,
что наименьшее значение функции
![]() на отрезке
на отрезке![]() равно
равно![]() ,
а наибольшее значение — равно
,
а наибольшее значение — равно![]() .
●
.
●
8.1.4. Выпуклость функции
Дифференцируемая
функция
![]() называетсявыпуклой
вверх
(вниз)
на интервале
называетсявыпуклой
вверх
(вниз)
на интервале
![]() ,
если график функции находится под (над)
касательной, проведенной в любой точке
интервала
,
если график функции находится под (над)
касательной, проведенной в любой точке
интервала![]() ,
т.е. для любой точки
,
т.е. для любой точки![]() выполняется условие:
выполняется условие:
![]()
![]()
![]() .
Заметим, что
.
Заметим, что
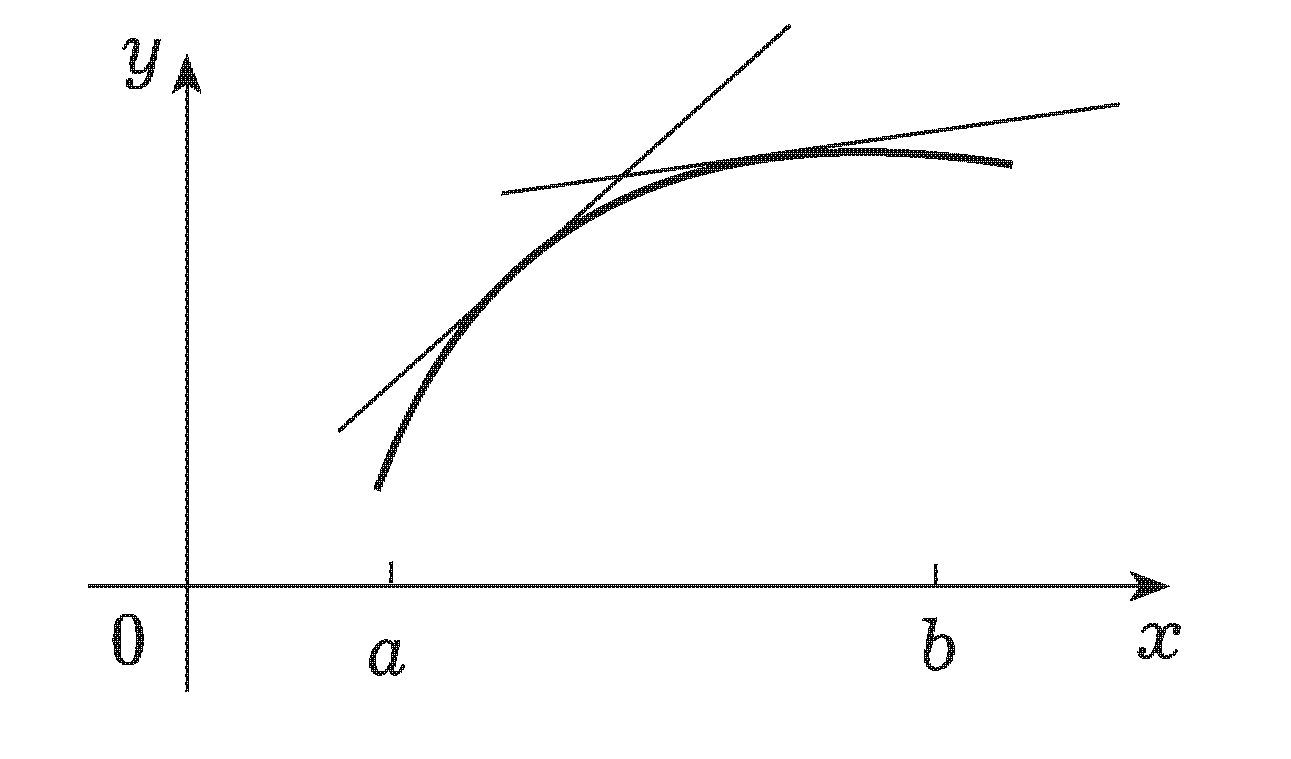
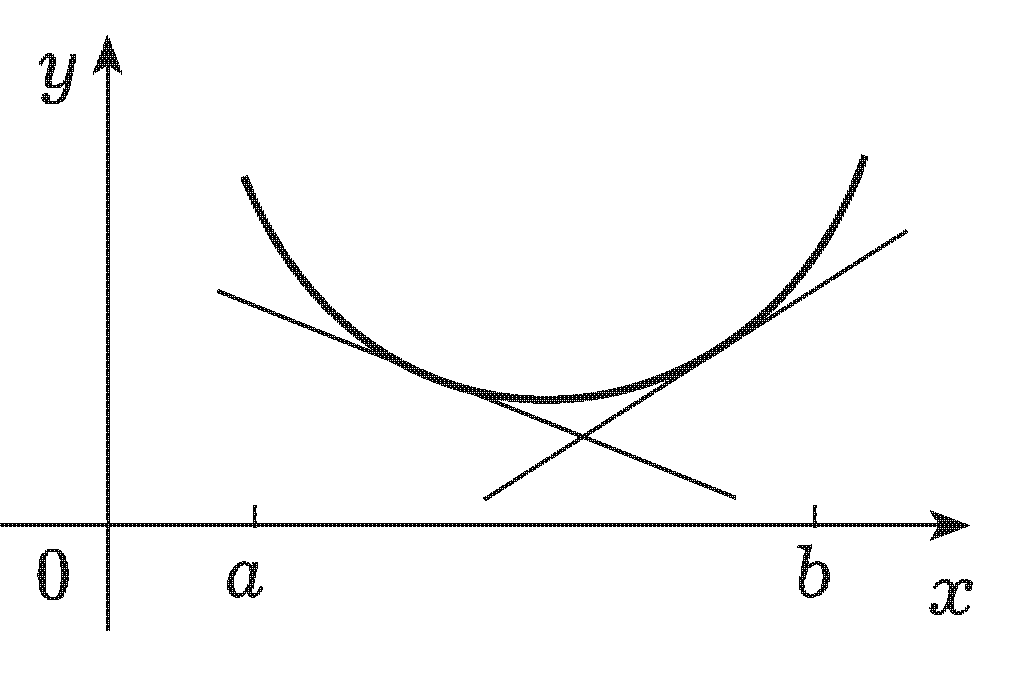
Рис. 8.1 Рис. 8.2
![]() является уравнением
касательной к графику функции
является уравнением
касательной к графику функции
![]() в точке
в точке![]() .
На рис. 8.1 (8.2) функция выпукла вверх
(вниз).
.
На рис. 8.1 (8.2) функция выпукла вверх
(вниз).
Теорема 8.4.
Функция
![]() дифференцируема на интервале
дифференцируема на интервале![]() .
Следующие
условия равносильны.
.
Следующие
условия равносильны.
1. Функция
![]() выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
![]() .
.
2. Производная
![]() не возрастает
(не убывает)
на интервале
не возрастает
(не убывает)
на интервале
![]() .
.
Доказательство
1![]() 2.Возьмем на
интервале
2.Возьмем на
интервале
![]() произвольные точки
произвольные точки
![]() .
Проведем
.
Проведем
касательную к
графику функции
![]() в точке
в точке![]() .
Тогда из выпуклости функции вверх (вниз)
следует
.
Тогда из выпуклости функции вверх (вниз)
следует
![]()
![]() (2)
(2)
Теперь проведем
касательную к графику функции
![]() в точке
в точке![]() .
Тогда из выпуклости функции вверх (вниз)
следует
.
Тогда из выпуклости функции вверх (вниз)
следует
![]()
![]() .
(3)
.
(3)
Сложим неравенства (2) и (3), и после простых преобразований получим
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Итак, если
![]() ,
то
,
то![]()
![]() ,
т.е. производная
,
т.е. производная![]() является невозрастающей (неубывающей)
функцией.
является невозрастающей (неубывающей)
функцией.
2![]() 1.Возьмем
произвольную точку
1.Возьмем
произвольную точку
![]() на интервале
на интервале![]() и покажем, что график функции находится
под (над) касательной, проведенной в
точке
и покажем, что график функции находится
под (над) касательной, проведенной в
точке![]() ,
т.е.
,
т.е.![]()
![]() для любой точки
для любой точки![]() .
Возможны два случая:
.
Возможны два случая:
![]() или
или
![]() .
.
Если
![]() ,
то, применяя теорему Лагранжа на отрезке
,
то, применяя теорему Лагранжа на отрезке![]() ,
получим
,
получим
![]() ,
,
![]()
![]() .
(4)
.
(4)
Так как производная
![]() является невозрастающей (неубывающей)
функцией, то из
является невозрастающей (неубывающей)
функцией, то из![]() следует
следует![]()
![]() .
Отсюда и равенства (4) имеем
.
Отсюда и равенства (4) имеем
![]()
![]()
![]()
![]()
![]() .
.
Если же
![]() ,
то, применяя теорему Лагранжа на отрезке
,
то, применяя теорему Лагранжа на отрезке![]() ,
получим
,
получим
![]() ,
,
![]()
![]() .
(5)
.
(5)
Так как производная
![]() является невозрастающей (неубывающей)
функцией, то из неравенства
является невозрастающей (неубывающей)
функцией, то из неравенства![]() следует
следует![]()
![]() .
Отсюда и равенства (5) имеем
.
Отсюда и равенства (5) имеем
![]()
![]()
![]()
![]()
![]() .
■
.
■
Следствие.
Функция
![]() дважды дифференцируема на интервале
дважды дифференцируема на интервале![]() .
Тогда равносильны условия.
.
Тогда равносильны условия.
1.
Функция
![]() выпукла вверх
(вниз)
на
интервале
выпукла вверх
(вниз)
на
интервале
![]() .
.
2. Вторая
производная неположительна (неотрицательна)
на интервале
![]() .
.
Доказательство. Используя теорему 8.4 и второе утверждение теоремы 8.1, в котором роль функции играет производная, получим следующую цепочку равносильных утверждений:
функция
![]() выпукла вверх
(вниз)
на интервале
выпукла вверх
(вниз)
на интервале
![]()
![]()
![]() производная
производная
![]() не возрастает (не убывает) на интервале
не возрастает (не убывает) на интервале
![]()
![]()
![]() производная
производная
![]()
![]() на интервале
на интервале
![]() .
■
.
■
Примеры
1. Функция
![]() выпукла вверх на интервале
выпукла вверх на интервале![]() ,
так как
,
так как
![]()
![]() .
.
2. Функция
![]() выпукла вниз на интервале
выпукла вниз на интервале![]() ,
так как
,
так как
![]()
![]() .
●
.
●
Точка
![]() называетсяточкой
перегиба графика
дифференцируемой функции
называетсяточкой
перегиба графика
дифференцируемой функции
![]() ,
если найдется такая окрестность
,
если найдется такая окрестность![]() этой точки, что на одном из интервалов
этой точки, что на одном из интервалов![]() ,
,![]() функция выпукла вверх, а на другом
выпукла вниз.
функция выпукла вверх, а на другом
выпукла вниз.
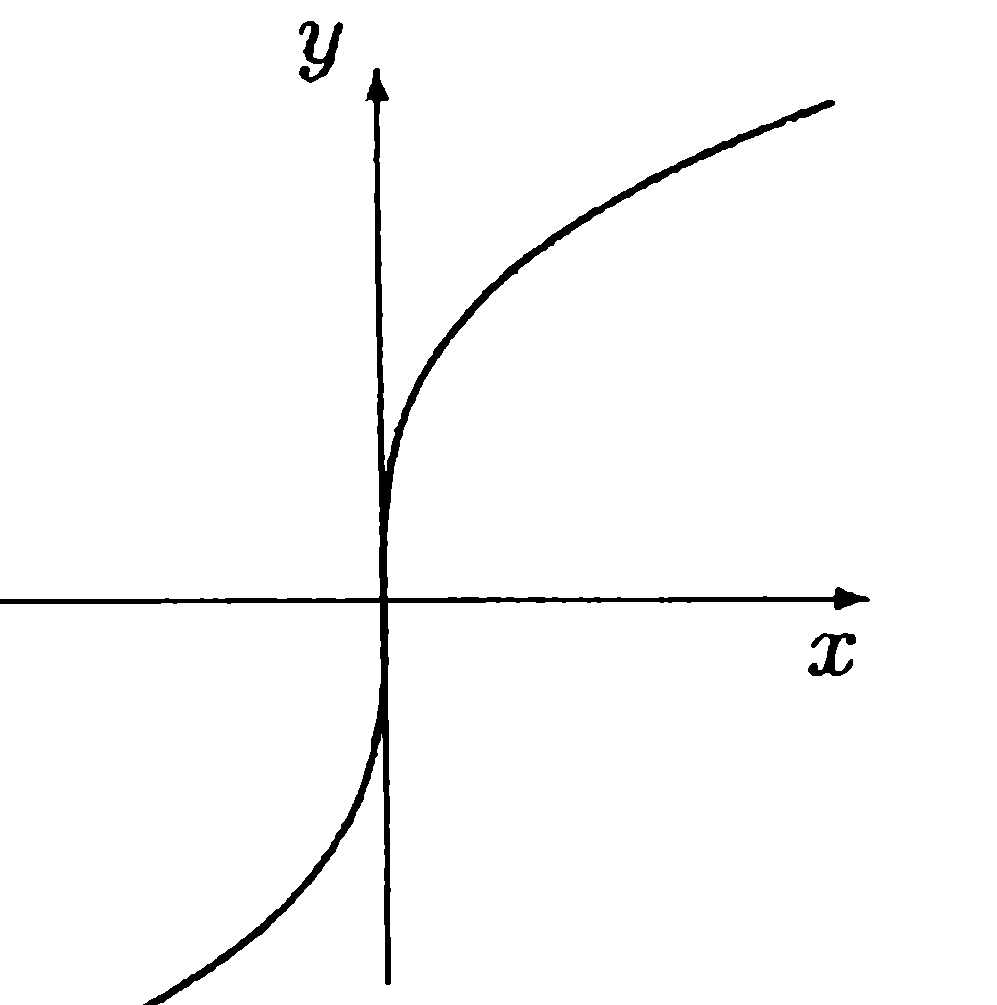
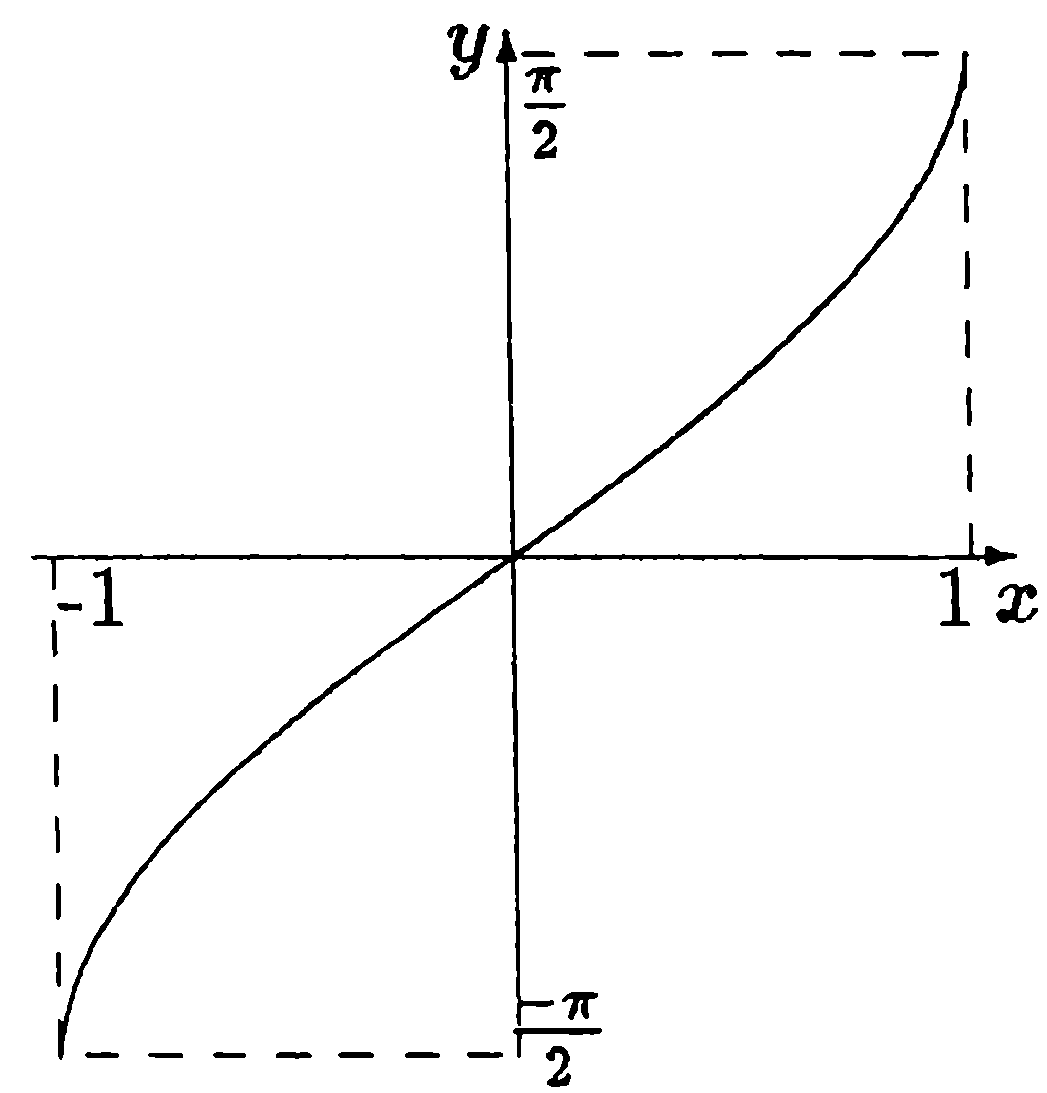
Рис. 8.3 Рис. 8.4
На рис. 8.3 точка
![]() является точкой перегиба графика функции
является точкой перегиба графика функции![]() ,
а на рис. 8.4 точка
,
а на рис. 8.4 точка![]() — точка перегиба графика функции
— точка перегиба графика функции
![]() .
Ниже эти утверждения будут доказаны.
.
Ниже эти утверждения будут доказаны.
Теорема 8.5.
Функция
![]() в точке
в точке![]() имеет непрерывную вторую производную.
Если
имеет непрерывную вторую производную.
Если![]() —
точка перегиба функции
—
точка перегиба функции![]() ,
то
,
то![]() .
.
Доказательство
теоремы
проведем методом от противного, т.е.
предположим, что
![]() .Тогда
.Тогда
![]() или
или![]() .
.
Если
![]()
![]() ,
то из теоремы 4.3 следует, что найдется
окрестность
,
то из теоремы 4.3 следует, что найдется
окрестность![]() точки
точки![]() ,
в которой
,
в которой
![]()
![]() .
Отсюда и из следствия к теореме 8.3
вытекает, что в этой окрестности
.
Отсюда и из следствия к теореме 8.3
вытекает, что в этой окрестности![]() выпукла вниз (вверх), т.е.
выпукла вниз (вверх), т.е.![]() не является точкой перегиба графика
функции
не является точкой перегиба графика
функции![]() .
Противоречие. ■
.
Противоречие. ■
Функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() .
Ее первая производная
.
Ее первая производная![]() в точке
в точке![]() равна 1, а вторая производная
равна 1, а вторая производная![]() в этой точке равна нулю. Так как слева
(справа) от точки
в этой точке равна нулю. Так как слева
(справа) от точки![]() функция
функция![]() (
(![]() ,
то из следствия к теореме 8.4 получаем,
что слева от точки
,
то из следствия к теореме 8.4 получаем,
что слева от точки![]() функция выпукла вверх, а справа — функция
выпукла вниз (рис. 8.4).
функция выпукла вверх, а справа — функция
выпукла вниз (рис. 8.4).
Заметим, что
условие
![]() является необходимым условием наличия
в точке
является необходимым условием наличия
в точке
![]() перегиба у кривой, но не является
достаточным условием, т.е. из условия
перегиба у кривой, но не является
достаточным условием, т.е. из условия
![]() не следует в общем случае, что точка
не следует в общем случае, что точка
![]() — точка перегиба графика функции
— точка перегиба графика функции![]() .
.
Например, вторая
производная функции
![]() ,
равная
,
равная![]()
![]() ,
обращается в нуль в точке
,
обращается в нуль в точке![]() .
Эта точка не является точкой перегиба,
так как из условия
.
Эта точка не является точкой перегиба,
так как из условия![]() и следствия к теореме 8.4 функция
и следствия к теореме 8.4 функция![]() выпукла вниз на всей числовой оси.
выпукла вниз на всей числовой оси.
В точке перегиба
функции
![]() функция
функция![]() может быть не определена. Рассмотрим
функцию
может быть не определена. Рассмотрим
функцию![]() ,
которая определена на всей числовой
прямой. Ее вторая производная
,
которая определена на всей числовой
прямой. Ее вторая производная![]() не существует в точке
не существует в точке![]() .
Так как на интервале
.
Так как на интервале![]() функция
функция![]() ,
а на интервале
,
а на интервале![]() —
—![]() ,
то на интервале
,
то на интервале![]() функция выпукла вниз, а на интервале
функция выпукла вниз, а на интервале![]() функция выпукла вверх (следствие из
теоремы 8.4). Следовательно, точка
функция выпукла вверх (следствие из
теоремы 8.4). Следовательно, точка![]() является точкой перегиба графика функции
является точкой перегиба графика функции![]() (рис. 8.3).
(рис. 8.3).
Только точки,
в которых вторая производная равна
нулю или не существует, могут быть
точками перегиба графика функции
![]() .
Эти точки называются критическими
точками 2-го рода.
.
Эти точки называются критическими
точками 2-го рода.
В нижеследующей теореме приводится условие, при котором критические точки 2-го рода являются точками перегиба графика функции.
Теорема 8.6.
Функция
![]() имеет в окрестности точки
имеет в окрестности точки![]() вторую производную
вторую производную![]() ,
кроме,
возможно,
самой точки
,
кроме,
возможно,
самой точки
![]() .
Если при переходе
.
Если при переходе![]() через точку
через точку![]() знак
знак![]() меняется, то точка
меняется, то точка![]() — точка перегиба графика функции
— точка перегиба графика функции![]() .
.
Доказательство.
Из следствия к теореме 8.4 следует, что
при переходе
![]() через точку
через точку![]() меняется выпуклость вверх кривой на
выпуклость вниз или наоборот. Отсюда
следует, что
меняется выпуклость вверх кривой на
выпуклость вниз или наоборот. Отсюда
следует, что![]() —точка
перегиба графика функции
—точка
перегиба графика функции
![]() .■
.■
Примеры. Найти
точки перегиба и интервалы выпуклости
кривой
![]() :
:
7.
![]() ,
8.
,
8.![]() .
.
Решение
1. Функция
![]() определена на всей числовой оси. Ее
вторая производная равна
определена на всей числовой оси. Ее
вторая производная равна![]() .
Находим критические точки 2-го рода:
.
Находим критические точки 2-го рода:![]() .
Эта точка разбивает область определения
на два интервала:
.
Эта точка разбивает область определения
на два интервала:
![]() ,
,
![]() .
В первом интервале производная
.
В первом интервале производная
![]() отрицательна, а во втором — положительна.
Следовательно,
отрицательна, а во втором — положительна.
Следовательно,![]() является точкой перегиба кривой
является точкой перегиба кривой![]() .
Она выпукла вверх на интервале
.
Она выпукла вверх на интервале![]() ,
а на интервале
,
а на интервале
![]() выпукла
вниз.
выпукла
вниз.
8. Функция
![]() определена
на всей числовой оси. Вторая производная
этой функции равна
определена
на всей числовой оси. Вторая производная
этой функции равна![]() .
Находим критические точки 2-го рода:
.
Находим критические точки 2-го рода:![]() .
Эти точки разбивают область определения
функции на три интервала:
.
Эти точки разбивают область определения
функции на три интервала:
![]() ,
,![]() ,
,![]() .
В первом и третьем интервалах производная
.
В первом и третьем интервалах производная
![]() положительна, а во втором — отрицательна.
Следовательно,
положительна, а во втором — отрицательна.
Следовательно,![]() являются точками перегиба данной кривой.
Она выпукла вверх на интервале
являются точками перегиба данной кривой.
Она выпукла вверх на интервале![]() ,
а на интервалах
,
а на интервалах![]() и
и![]() выпукла вниз.
выпукла вниз.
