§ 8.2. Экстремумы функций нескольких переменных

8.2.1. Необходимое условие экстремума

Функция определена на множествеи точка. Функцияимеетлокальный экстремум в точке , если найдется окрестность

этой точки, в которой справедливо неравенство

или .

В первом случае точка называется точкойлокального минимума, а во втором — точкой локального максимума.

Заметим, что будет точкой локального минимума (максимума) тогда и только тогда, когда в некоторой окрестности этой точки

.

Теорема 8.7 (необходимое условие экстремума). Функция имеет в точкелокальный экстремум. Тогда градиент функциив точкеравен нулевому вектору.

Доказательство. Так как

,

то для доказательства теоремы достаточно доказать, что все частные производные функции в точкеравны нулю. Полагаем значения всех переменных у функцииравными соответствующим координатам точки , кроме переменной . Тогда получим функцию, которая зависит от одной переменной и имеет в точкелокальный экстремум. Из теоремы 8.2 следует, что

, . ■

Точки, в которых градиент функции равен нулевому вектору, называются критическими точками функции. Так же, как и в случае функции одной переменной, не каждая критическая точка функции многих переменных является точкой локального экстремума функции.

Примеры

Найти критические точки функции:

1. ; 2..

Решение

1. После того, как найдем частные производные и приравняем их нулю, получим систему уравнений

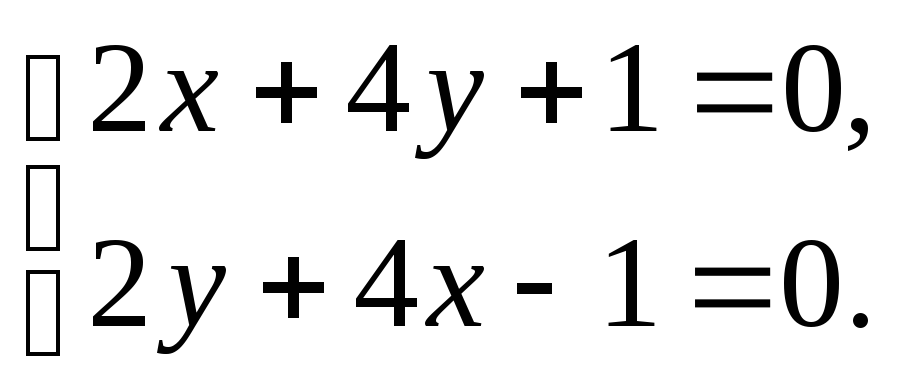
Решение этой системы уравнений является критической точкой функции.

2. Критическую точку функции находим из условий равенства нулю частных производных. Получаем систему уравнений

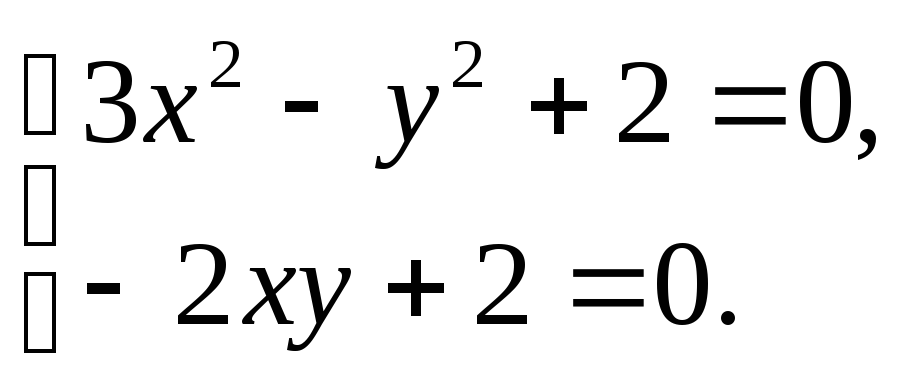
Решения иэтой системы уравнений являются критическими точками функции. ●

8.2.2. Достаточное условие экстремума функции

Исследование поведения функции в окрестности точки проведем, используя формулу Тейлора в форме Пеано (теорема 7.1):

, (1)

где ,,.

Второй дифференциал

(2)

функции в точкеявляется квадратичной функцией от переменных,, а числа — коэффициенты этой квадратичной функции.

Квадратичная функция называется положительно (отрицательно) определенной, если значение этой функции при любых значениях приращений , одновременно не равных нулю, положительно (отрицательно).Знакопостоянной будем называть квадратичную функцию, которая является положительно или отрицательно определенной. Знакопеременной называется квадратичная функция, которая принимает как положительные, так и отрицательные значения.

Лемма 1 . Если функция является знакопостоянной и

, то найдется такое число , что знак выражения

(3)

совпадает со знаком функции , если .

Доказательство. Перепишем формулу (2) в виде

.

Так как

,

то точка при любых значениях,…,,…,, одновременно не равных нулю, принадлежит сфере.

Квадратичная функция непрерывна при любых значениях

переменных, и значит, непрерывна на сфере, которая является замкнутым и ограниченным множеством (следствие из теоремы 4.9) . Так как функция является знакоопределенной, то >0 в каждой точке сферы.

Из 2-й теоремы Вейерштрасса следует, что функция принимает свое наименьшее значениев некоторой точке сферы, которое больше нуля, т.е.. Отсюда следует, что

. (4)

Так как , то из теоремы 3.11 вытекает, что если, то найдется такое число, что неравенствобудет справедливо, как только . Отсюда следует, что

.

Следовательно, знак выражения совпадает со знаком , как только . ■

Лемма 2. Точка , , принадлежит окрестноститогда и только тогда, когда.

Доказательство вытекает из следующей цепочки равносильных утверждений:

. ■

Теорема 8.8 (достаточное условие экстремума). Функция в окрестности критической точкиимеет непрерывные частные производные 2-го порядка. Справедливы следующие утверждения:

1. Если функция положительно определена, то — точка локального минимума функции.

2. Если функция отрицательно определена, то — точка локального максимума функции.

Доказательство. Градиент функции в точке равен нулю, так

как является критической точкой этой функции. В этом случае формула (1) будет иметь вид

.

Из леммы 1 и 2 следует, что найдется такая окрестность , в которой знак приращенияфункции совпадает со знаком второго дифференциала в точке этой функции.

1. Если функция положительно определена, то в окрестноститочки , т.е. в этой окрестности, значит,— точка локального минимума функции.

2. Если функция отрицательно определена, то в окрестноститочки , т.е. в этой окрестности, значит,— точка локального максимума функции. ■

Ниже докажем, что если функция является знакопеременной, то не является точкой локального экстремума. При доказательстве этого утверждения необходимо будет иметь явную зависимостьот вектора приращений. Для этого введем обозначение

.

Тогда приращение функции в критической точке будет иметь вид

, ,.

Лемма 3. Справедливы следующие утверждения, где .

1. Для любого числа верно, что .

2. Если ,, и , то найдется такое число, что неравенство

, .

будет справедливо, как только .

Доказательство

1. .

2. Так как , то. Используя 1-е утверждение леммы 3, получим

.

Отсюда и из 1-го утверждения леммы 1 следует 2-е утверждение леммы 3. ■

Теорема 8.9. Если функция является знакопеременной, то не является точкой локального экстремума.

Доказательство. Допустим противное, т.е. пусть является точкой локального экстремума функции. Тогда из определения локального максимума (минимума) следует, что найдется окрестностьточки, в каждой точки которой выполняется неравенство.

Так как функция является знакопеременной, то существует такой вектор приращений, что.

Рассмотрим вектор приращений ,. Из леммы 3 следует, что

найдется такое число , что если, то справедливо неравенство

. (5)

Обозначим символом . Тогда.

Если , то. Отсюда получаем, что выполняется неравенство (5), и, значит, справедливо неравенство

. (6)

Если , то. Теперь из леммы 2 вытекает, что точка, , принадлежит окрестности .

Из неравенства (6) следует , и. Значит, точкане является точкой локального максимума (минимума) функциив окрестности, что противоречит сделанному предположению. ■

Пусть функция имеет непрерывные производные второго порядка в окрестности точки. Тогда из теоремы о смешанных производных 7.1 следует, чтопри любых значенияхиотдо. Если ввести обозначения:, , то второй дифференциал будет иметь вид

, . (7)

Квадратичная функция (7) называется квадратичной формой.

Знакоопределенность и знакопеременность квадратичной формы можно установить при помощи приведения квадратичной формы к сумме квадратов. Каждая квадратичная форма может быть методом выделения полных квадратов приведена к виду (приложение 3)

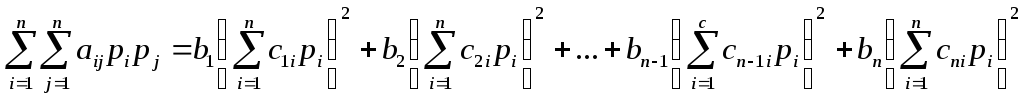. (8)

Справедливы следующие утверждения:

1. квадратичная форма (7) положительно определена тогда и только тогда, когда все коэффициенты в равенстве (8) положительны, т.е.

, , … ,.

2. квадратичная форма (7) отрицательно определена тогда и только тогда, когда все коэффициенты в равенстве (8) отрицательны, т.е.

, , … ,.

3. квадратичная форма является знакопеременной тогда и только тогда, когда среди коэффициентов в равенстве (8) имеется хотя бы два коэффициента разных знаков.

В качестве примера рассмотрим приведение к сумме квадратов второго дифференциала функции, имеющей непрерывные вторые производные. В этом случае процесс приведенияк сумме квадратов имеет вид (:

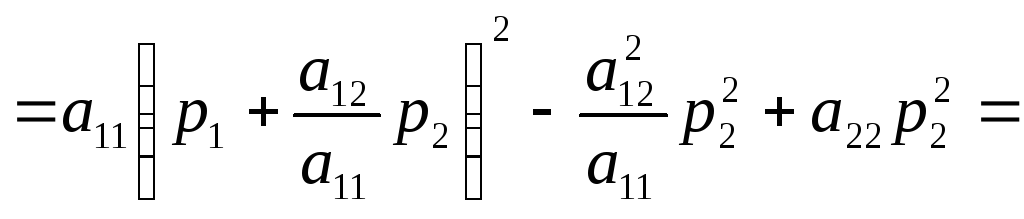
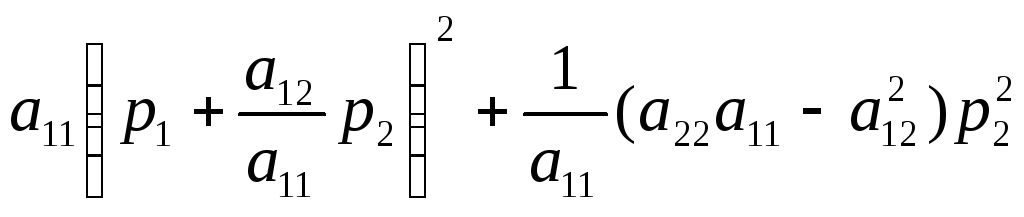. (9)

Отсюда следует, что если

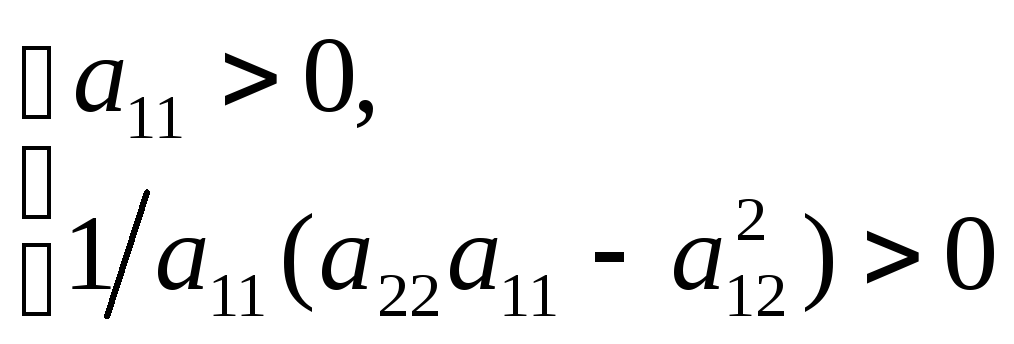
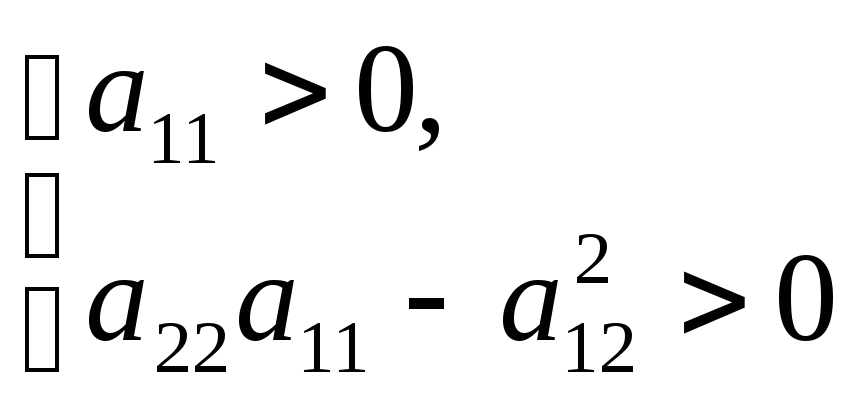
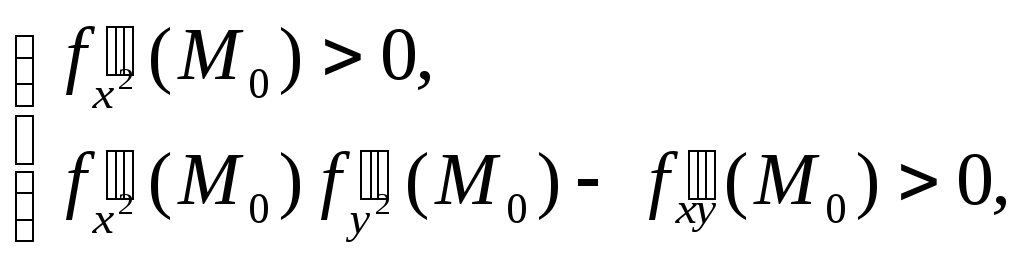(10)

то квадратичная форма положительно определена и, значит, в точке

функция имеет локальный минимум, а если

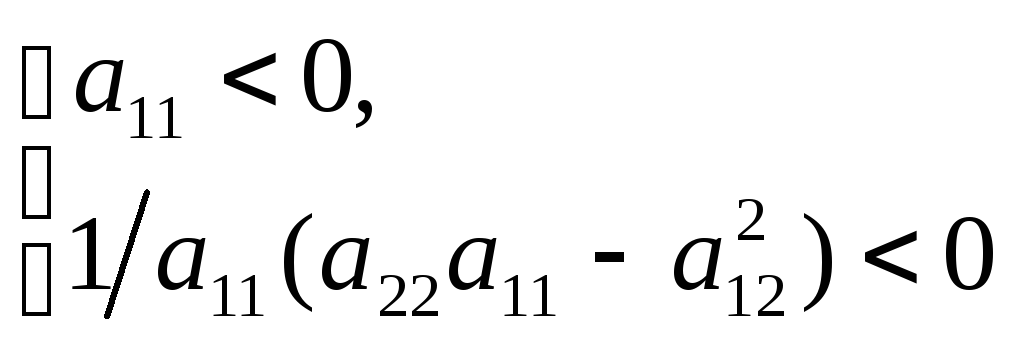
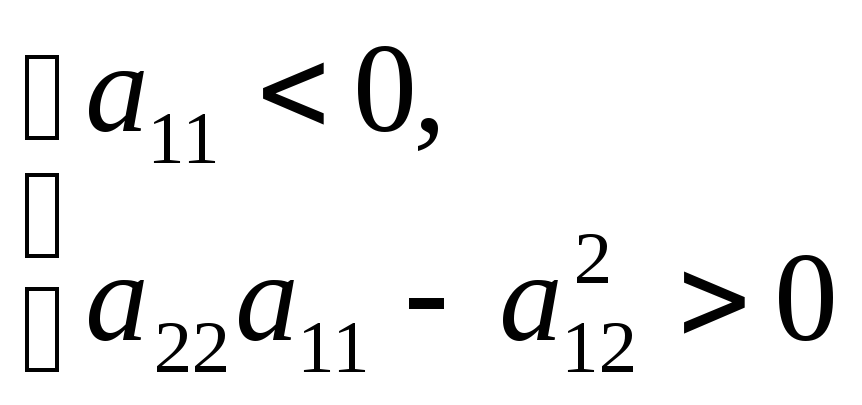
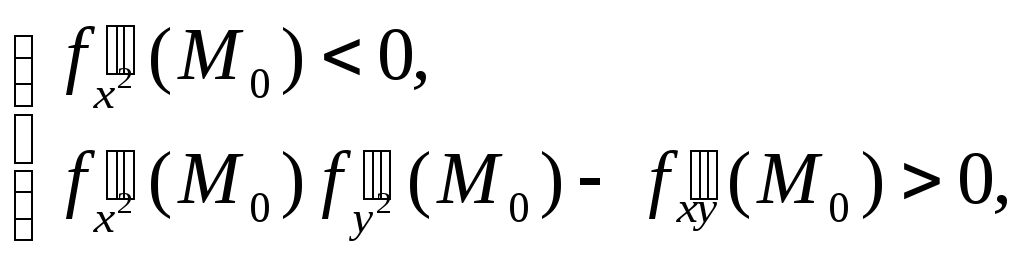(11)

то квадратичная форма отрицательно определена и, значит, в точке

функция имеет локальный максимум.

Если же выполняется условие

, (12)

то знаки коэффициентов при квадратах в выражении (8) будут разными, каков бы ни был знак числа . Следовательно, если выполняется условие (12), то квадратичная формабудет знакопеременной и в точкефункцияне имеет локального экстремума.

Критерий Сильвестра. Установить знакоопределенность квадратичной формы можно также при помощи критерия Сильвестра: квадратичная форма

, ,

а) положительно определена тогда и только тогда, когда

, , ,…, ;

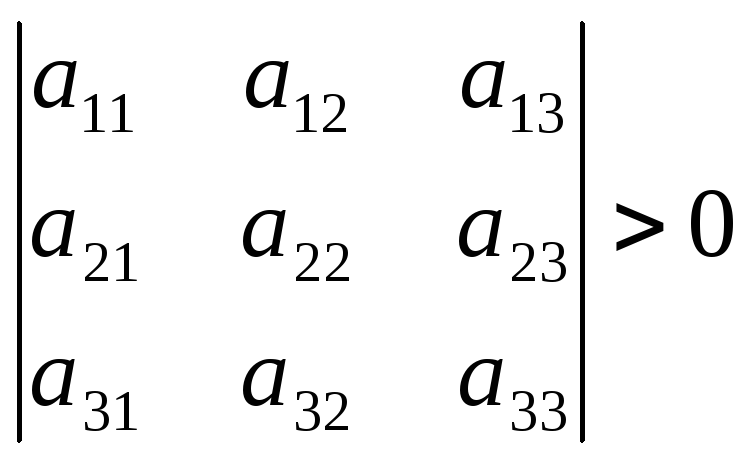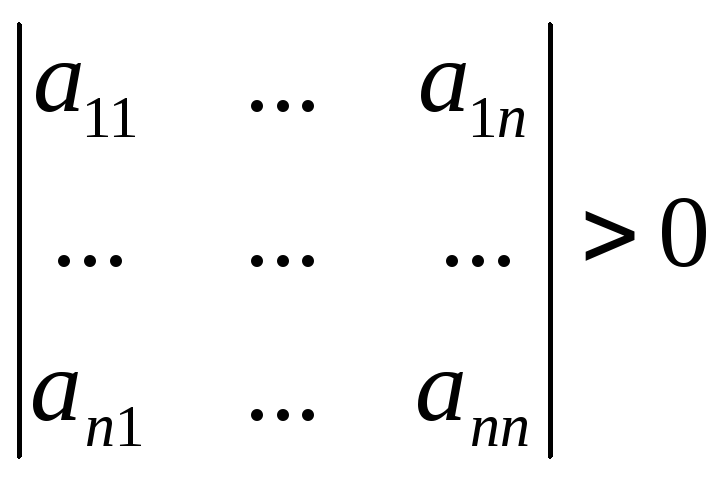б) отрицательно определена тогда и только тогда, когда

, , ,…, ,

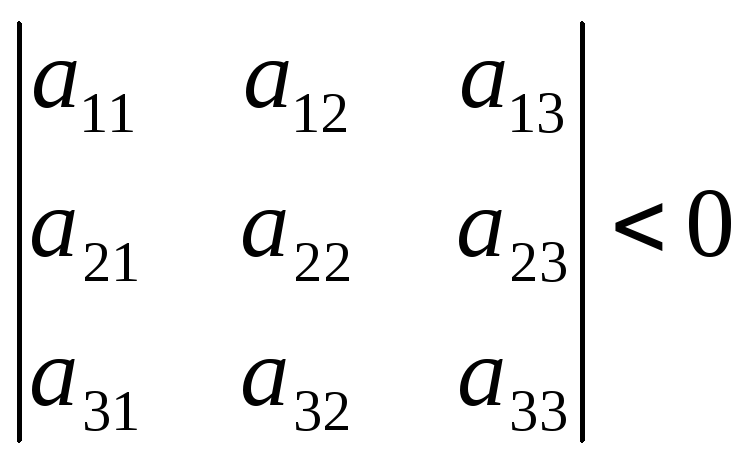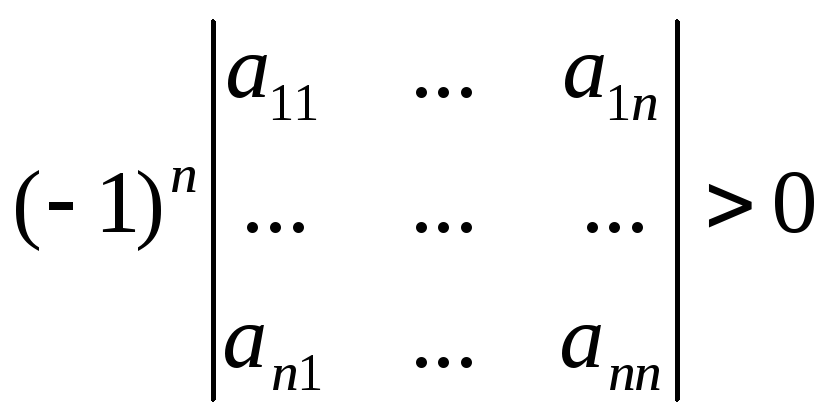в) является знакопеременной, если

.

Примеры. Исследовать на экстремум функции.

3. .

4. .

Решение

3. а). Находим критические точки функции, т.е. точки, в которых частные производные первого порядка равны нулю:

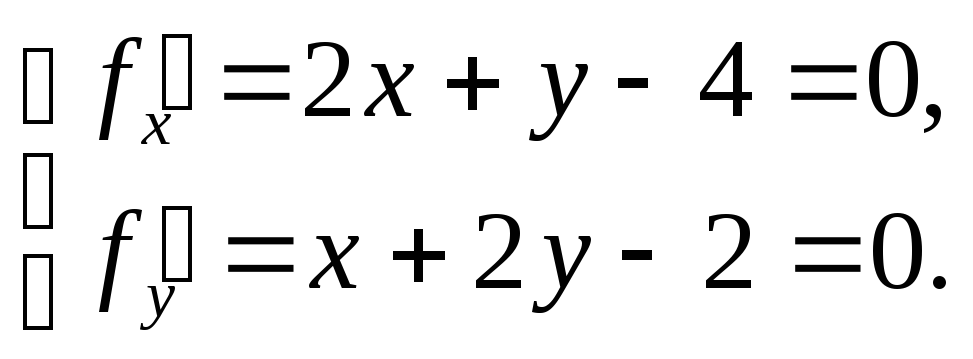
Решением этой системы является ,, поэтому точка— единственна критическая точка функции.

б). Вычислим вторые производные функции в точке :

, , .

Значения вторых производных не зависят от координат точки .

в). Проверим выполнение достаточного условия для точки . Начнем с определения знака выражения:

. (13)

Так как , то из условий (13) и (10) следует, что в точкефункция имеет локальный минимум.

4. а) Находим критические точки функции, т.е. точки, в которых частные производные первого порядка равны нулю:

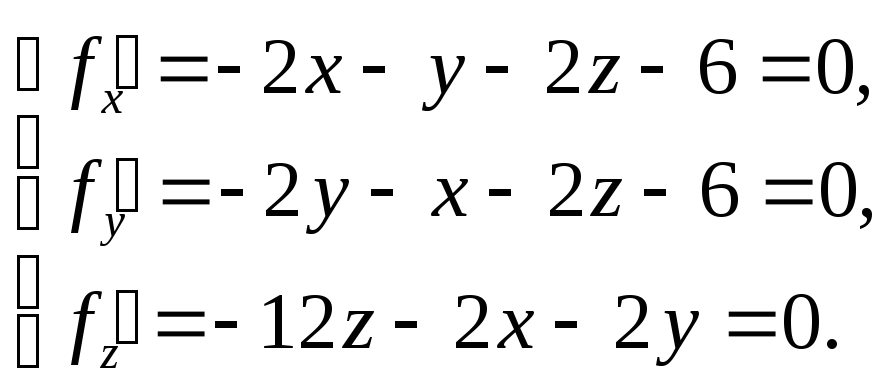
Решением этой системы является тройка чисел ,,, поэтому точка— единственна критическая точка функции.

б). Вычислим вторые производные функции в точке:

, , , , , , .

Значения вторых производных не зависят от координат точки .

в) Проверим выполнение достаточного условия для точек . Найдем знаки определителей (приложение 4):

, ,

.

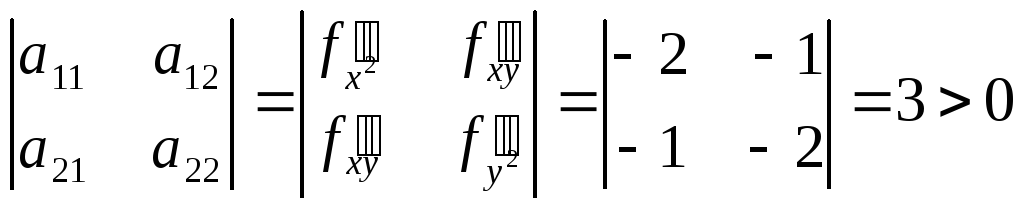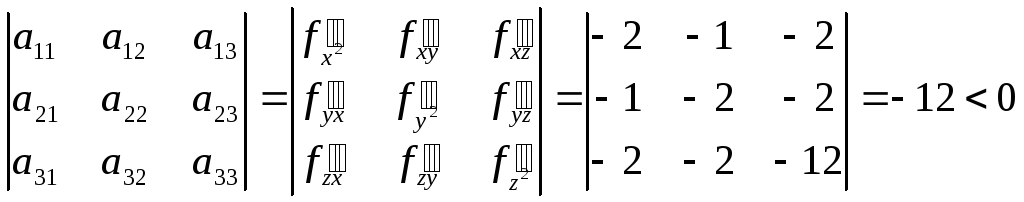Отсюда следует, что является отрицательно определенной квадратичной формой. Следовательно, в точкефункция имеет локальный максимум. ●

Замечание. Непрерывная функция может иметь локальный экстремум в точках, в которых функция не дифференцируема. Например, точка — локальный минимум функции, но в этой точке функция не имеет частных производных. На рис. 3.2 приведен график этой функции. ▲

Задачи

Исследовать на экстремум функции.

1. . 2..

3. . 4. .

5. . 6.

7. . 8..