
- •Глава 8. Исследование поведения функций
- •§ 8.1. Исследование поведения функций одной переменной
- •8.1.1. Условия монотонности функции
- •8.1.2. Локальные экстремумы функции
- •8.1.3. Наибольшее и наименьшее значение функции на отрезке
- •8.1.4. Выпуклость функции
- •8.1.5. Асимптоты графика функции
- •§ 8.2. Экстремумы функций нескольких переменных
- •8.2.1. Необходимое условие экстремума
- •8.2.2. Достаточное условие экстремума функции
- •§ 8.3. Глобальные экстремумы функции
- •8.3.1. Понятие глобального экстремума функции
- •8.3.2. Необходимое условие глобального экстремума
- •8.3.3. Метод Лагранжа отыскания
§ 8.3. Глобальные экстремумы функции
8.3.1. Понятие глобального экстремума функции
Рассмотрим
функцию
![]() ,
которая задана на замкнутом множестве
,
которая задана на замкнутом множестве![]() .
Точка
.
Точка![]() называется точкойглобального
максимума
или наибольшим
значением
функции на множестве
называется точкойглобального
максимума
или наибольшим
значением
функции на множестве
![]() ,
если
,
если
![]()
![]() .
.
Если же
![]()
![]() ,
то точка
,
то точка
![]() называется точкойглобального
минимума
или наименьшим
значением
функции на множестве
называется точкойглобального
минимума
или наименьшим
значением
функции на множестве
![]() .
.
Точка
![]() называется точкойглобального
экстремума
функции
называется точкойглобального
экстремума
функции
![]() на множестве
на множестве![]() ,
если точка
,
если точка![]() является глобальным минимумом или
глобальным максимумом функции
является глобальным минимумом или
глобальным максимумом функции![]() на множестве
на множестве![]() .
.
Если функция
непрерывна на замкнутом и ограниченном
множестве
![]() ,
то из теоремы Вейерштрасса следует,
что во множестве
,
то из теоремы Вейерштрасса следует,
что во множестве![]() найдутся точки глобального максимума
и минимума функции.
найдутся точки глобального максимума
и минимума функции.
Точки глобального
экстремума функции могут быть внутренними
точками множества
![]() или принадлежать границе множества
или принадлежать границе множества![]() .
Если точка глобального экстремума
является внутренней, то она является
локальным экстремумом функции.Отсюда
вытекает алгоритм отыскания глобальных
экстремумов функции
на множестве
.
Если точка глобального экстремума
является внутренней, то она является
локальным экстремумом функции.Отсюда
вытекает алгоритм отыскания глобальных
экстремумов функции
на множестве
![]() :
:
1. Во множестве
![]() найти все критические точки функции, а
также точки, в которых функция не
дифференцируема.
найти все критические точки функции, а
также точки, в которых функция не
дифференцируема.
2. Найти все точки,
в которых функция может принимать
наибольшее и наименьшее значения на
границе множества
![]() .
.
3. Вычислить значения функции в точках, найденных в пунктах 1 и 2.
4. Среди значений, найденных в пункте 3, выбрать наибольшее и наименьшее значения.
Примеры
1. Найти глобальный
экстремум функции
![]() на множестве
на множестве![]() .
.
Решение.
Множество
![]() является ограниченным, так
является ограниченным, так![]() и
и![]() .
Из теоремы 4.9. вытекает, что
.
Из теоремы 4.9. вытекает, что![]() является замкнутым множеством.
Следовательно функция
является замкнутым множеством.
Следовательно функция![]() на множестве
на множестве![]() имеет глобальный минимум и максимум.
Множество
имеет глобальный минимум и максимум.
Множество![]() представляет собой треугольник,
ограниченный осями координат и прямой
представляет собой треугольник,
ограниченный осями координат и прямой![]() (рис. 8.7).
(рис. 8.7).
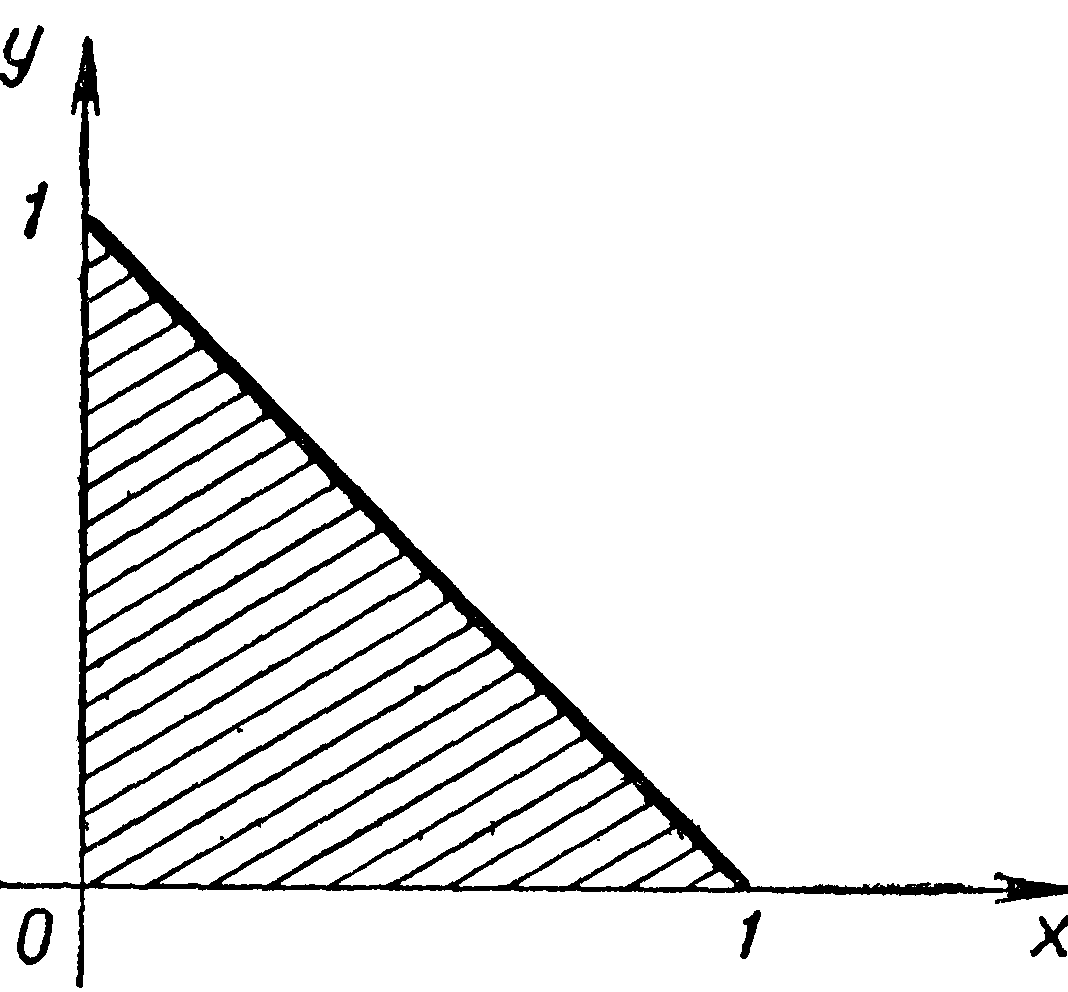
Рис.8.7.
Найдем критические
точки функции
![]() .
Так как
.
Так как
![]() ,
,
![]() ,
,
то функция
![]() имеет единственную критическую точку
имеет единственную критическую точку![]() ,
которая принадлежит множеству
,
которая принадлежит множеству![]() .
.
Исследуем функцию
на отрезке
![]() ,
,![]() .
Подставляя
.
Подставляя![]() в выражение для функции, получим
в выражение для функции, получим![]() .
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке
.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке![]() .
Отсюда следует, что на отрезке
.
Отсюда следует, что на отрезке![]() ,
,![]() функция принимает наименьшее и наибольшее
значение только в точках
функция принимает наименьшее и наибольшее
значение только в точках
![]() ,
,
![]() и
и![]() .
.
Исследуем функцию
на отрезке
![]() ,
,![]() .
Подставляя
.
Подставляя![]() в выражение для функции, получим
в выражение для функции, получим![]() .
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке
.
Функция принимает наименьшее и наибольшее
значение на концах отрезка и в критической
точке![]() .
Отсюда следует, что на отрезке
.
Отсюда следует, что на отрезке![]() ,
,![]() функция принимает наименьшее и наибольшее
значение только в точках
функция принимает наименьшее и наибольшее
значение только в точках
![]() ,
,
![]() и
и![]() .
.
Исследуем функцию
на отрезке
![]() ,
,![]() .
Подставляя
.
Подставляя![]() в выражение для функции, получим
в выражение для функции, получим
![]() .
.
Функция принимает
наименьшее и наибольшее значение на
концах отрезка и в критической точке
![]() .
Отсюда следует, что на отрезке
.
Отсюда следует, что на отрезке![]() ,
,![]() функция принимает наименьшее и наибольшее
значение только в точках
функция принимает наименьшее и наибольшее
значение только в точках
![]() ,
,
![]() и
и![]() .
.
В таблице 8.1 приведены значения функции во всех найденных точках.
Таблица 8.1
Из таблицы 8.1
следует, что
![]() и
и![]() —
точки соответственно глобального
минимума и максимума функция
—
точки соответственно глобального
минимума и максимума функция![]() ,
и
,
и
![]() ,
,
![]() .
●
.
●
Задачи
Найти глобальные
экстремумы функции
![]() на множестве
на множестве![]() .
.
1.
![]() ,
,![]() .
.
2.
![]() ,
,![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() ,
,![]() .
.
5.
![]() ,
,![]() .
.
Ответы
1.
![]() ,
,![]() .
.
2.
![]() ,
,![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() ,
,![]() .
.
5.
![]() ,
,![]() .
▲
.
▲
