Глава 2. Примеры решения задач Задача № 1
Предприятие специализируется по выпуску продукции трех видов P1,P2, иP3; при этом использует сырье трех типов:S1,S2иS3. Норма и объем расхода каждого типа сырья на 1 день заданы таблицей. Найти ежедневный объем выпуска каждого вида продукции.
Полученную систему уравнений решить матричным методом, методом Гаусса и методом Крамера.
|
Вариант№1. | ||||
|
Изделие |
Нормы расхода сырья у. е. |
Расход сырья на 1 день у. е. | ||
|
P1 |
P2 |
P3 | ||
|
S1 |
5 |
6 |
4 |
2700 |
|
S2 |
2 |
2 |
1 |
900 |
|
S3 |
3 |
4 |
2 |
1600 |
Решение
Пусть ежедневно фабрика выпускает x1штизделияS1,x2штизделияS2 иx3штизделияS3. Запишем это в видестолбца суточного выпуска продукции X. Далее выпишемматрицу технико-экономических коэффициентов A, а также столбецсуточного расхода сырья В
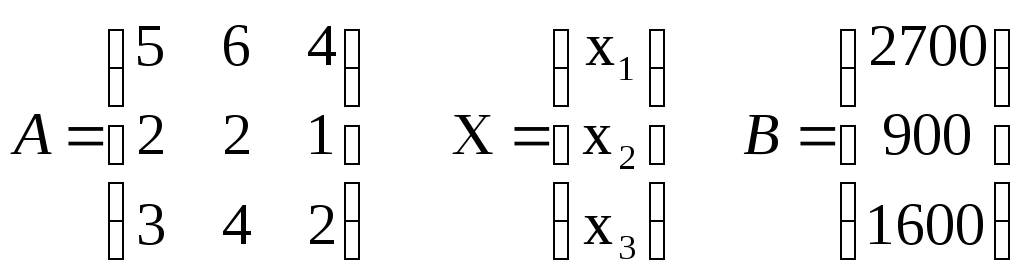
Найдем количество сырья S1 , затраченного на производство обуви:
.
Найдем количество сырья S2 , затраченного на производство обуви:
.
Найдем количество сырья S3 , затраченного на производство обуви:
.
В результате получаем следующую систему уравнений для определения суточного выпуска продукции:
Решение системы уравнений матричным методом.
1)Вычисляем определитель матрицыА, применяя теорему Лапласа к первой строке:
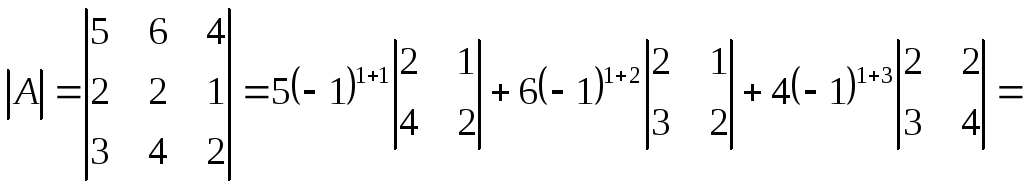
2)Выписываем транспонированную матрицуАТ:
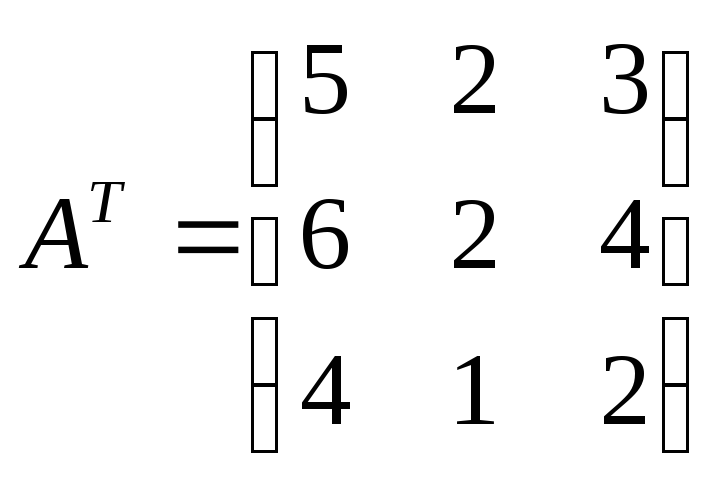
3)Строим присоединенную матрицу
.
Ее элементы представляют собой
алгебраические дополнения соответствующих
элементов транспонированной матрицыАТ.
Выписываем присоединенную матрицу:
4)Находим обратную матрицу по
формуле:
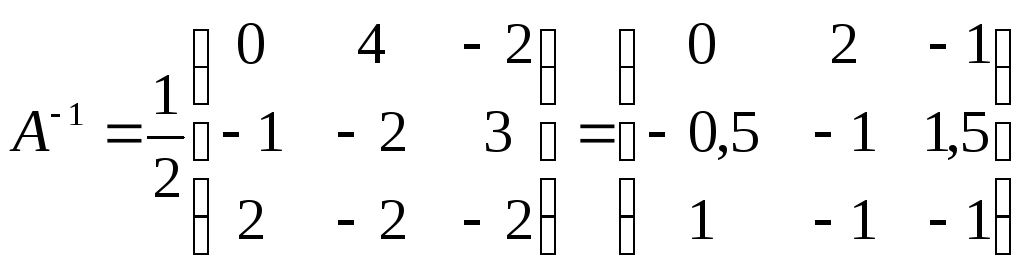
5)Вычисляем столбецX
по формуле:
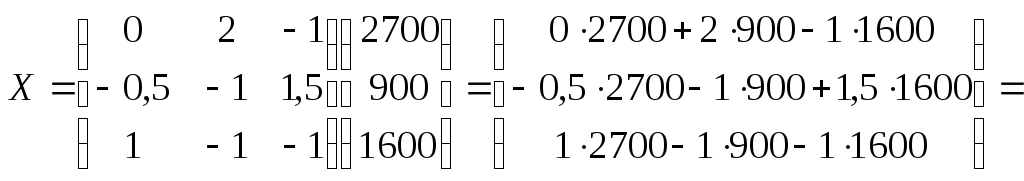
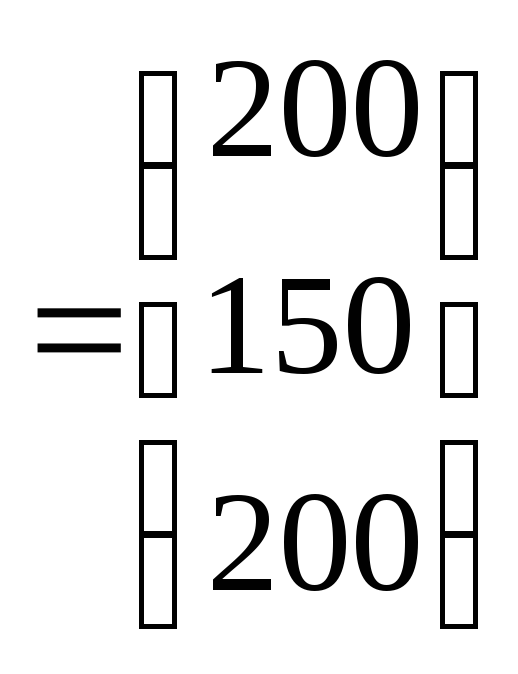
Решение окончено.
Решение системы уравнений методом Гаусса.
1. Пошаговый способ решения системы уравнений.
I шаг прямого хода:
1.1.Делим первое уравнение системы на коэффициент, стоящий передx1
1.2.Из второго уравнения вычитаем первое, умноженное на 2:
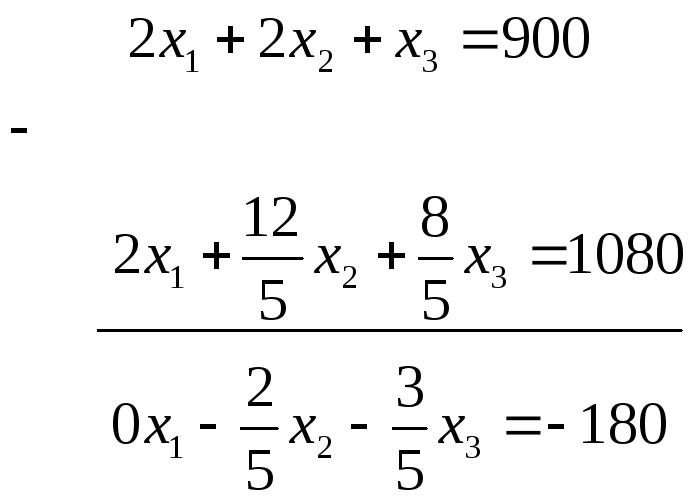
Или, умножая это уравнение на -5,
1.3.Из третьего уравнения вычитаем первое, умноженное на 3:
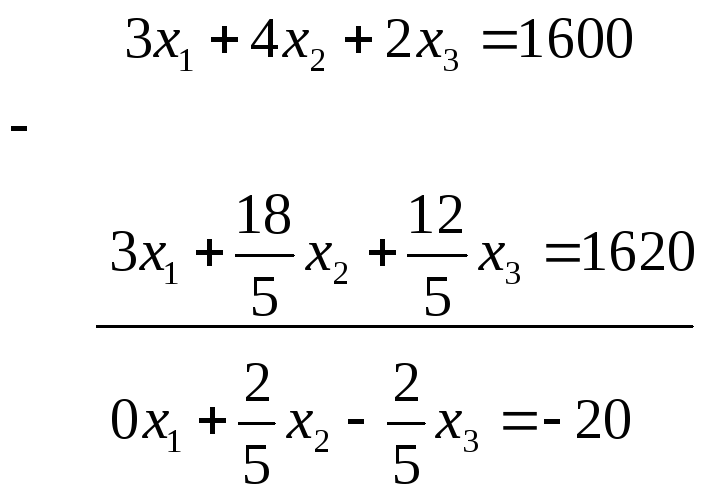
Или, умножая это уравнение на 5,
1.4.В результате получаем следующую систему уравнений:
II шаг прямого хода:
Из третьего уравнения вычитаем второе:
Обратный ход
Из второго уравнения получаем:
.
Из первого уравнения:
2. Способ решения с помощью расширенной матрицы.
Расширенная матрица системы имеет вид:
Шаг 1. Умножая первую строку расширенной матрицы на числа(-2/5), (-3/5) и прибавляя полученные строки соответственно ко второй , третей строке, исключаем переменную х1 из всех строк, начиная со второй
Получаем матрицу:
Шаг 2. Учитывая, что в полученной выше матрице а22=-а32складываем вторую и третью строки. Таким образом переменнаях2 исключается из третьей строки.
Получили расширенную матрицу треугольного вида:
,
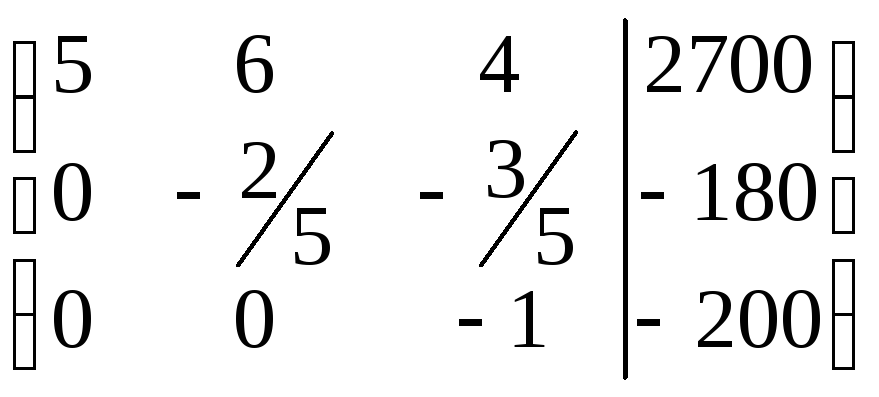которая соответствует равносильной
системе уравнений
,
откуда, используя обратный ход метода Гаусса(см.выше 1 способ), найдём из второго уравнения х2=150 ; из первого уравнениях1=200.
Замечание.Обратный ход метода Гаусса можно также провести с расширенной матрицей (треугольной формы) полученной системы. Для этого данную матрицу приводят к диагональному виду, что позволяет осуществить полное выделение переменных, удобное для их нахождения.
Если на прямом ходе с помощью первой, второй и т.д. строки мы добивались получения нулевых элементов ниже главной диагонали, то на обратном ходе с помощью последней, предпоследней и т.д. строки добиваемся получения нулевых элементов выше главной диагонали матрицы.
На примере данной задачи это будет выглядеть следующим образом:
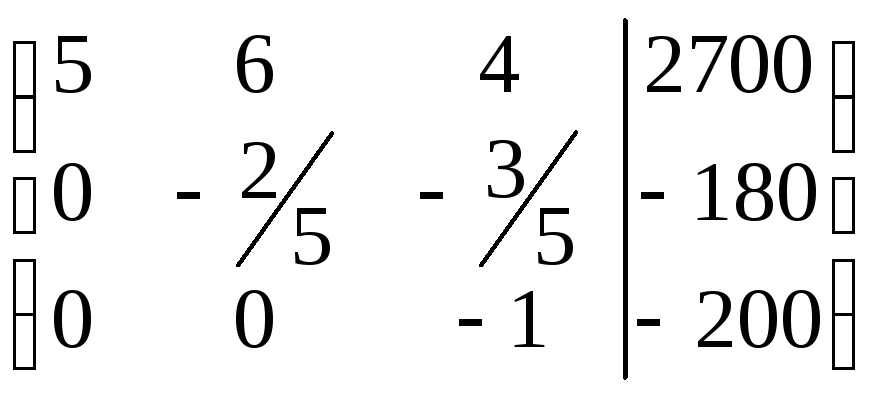
а) В полученной треугольной матрице умножаем третью строку
на (-3/5) и складываем со второй строкой, получаем равносильную матрицу:
б) умножаем третью строку последней матрицы на 4, вторую строку на 15. Полученные строки складываем с первой, получаем равносильную диагональную матрицу.
,
что равносильно системе уравнений
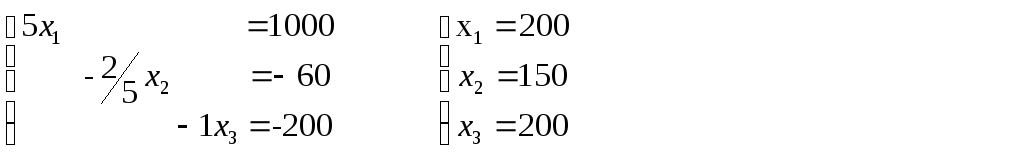
Решение окончено.