2.5. Динамические характеристики многомассовой механической системы

Во многих случаях кинематическая схема рабочей машины содержит упругие элементы: длинные валы, торсионы, упругие муфты, текстропные, канатные передачи и др.). В реальных схемах иногда приходится учитывать люфты и зазоры в зубчатых передачах и соединениях. В этих случаях кинематическую схему нельзя рассматривать как жесткую одномассовую систему. В особенности это касается высокоточных электроприводов и электроприводов, работающих в интенсивных динамических р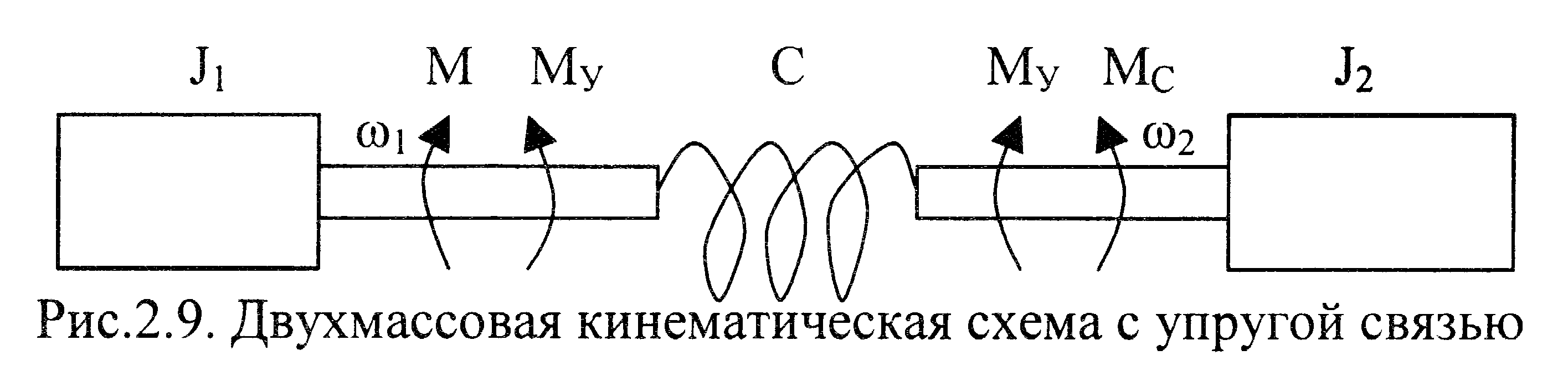ежимах.

Механические системы, в которых присутствуют явно выраженные упругие звенья, обычно приводят к двухмассовым или трехмассовым механическим системам. Рассмотрим двухмассовую электромеханическую схему (рис.2.9). В неразветвленной кинематической схеме обычно выделяют ротор двигателя и жестко связанные с нем элементы кинематической цепи. Приводя моменты инерции этих звеньев к скорости вала двигателя, получим первую массу J₁. Эта масса связана посредством упругого элемента, имеющего жесткость С, со второй массой J₂, которую образуют моменты инерции рабочего органа и жестко связанных с ним остальных элементов кинематической цепи.

Для составления расчетной механической схемы все моменты инерции звеньев, приложенные к ним моменты сопротивления движению М_Сi, упругость элементов и величины зазоров должны быть приведены к скорости вала двигателя. В упругом элементе возникают упругие моменты (усилия), которые выражаются законом Гука:

Для вращательного движения - ,

где: С – жесткость элемента, Н/рад;

- угол закручивания элемента (например, торсиона), рад;

Для поступательного движения ,

где: - растяжение элемента, м (С имеет размерность Н/м).

При деформации упругого элемента в нем запасается потенциальная энергия, которая соответственно для вращательного и поступательного движения равна:

Для приведения жесткости элемента к валу двигателя используется принцип равенства потенциальных энергий:

Если упругий элемент связан с поступательным движением, то его жесткость приводится по формуле

Будем считать (см. расчетную схему рис.2.9), что все элементы кинематической цепи приведены по своим параметрам к валу двигателя и разделены на две массы J₁ и J₂, связанные между собой упругим элементом с жесткостью С. К первой массе приложен момент двигателя М, ко второй – статический момент М_С.

Если затормозить второй вал, то возможно вращение первого вала в пределах, определяемых диапазоном упругой деформации элемента С. Если затормозить первый вал, то возможно с учетом указанного ограничения вращение второго вала. Таким образом, в отличие от одномассовой жесткой механической системы двухмассовая система обладает двумя степенями подвижности.

При анализе механических систем с двумя и более степенями подвижности целесообразно пользоваться математическим аппаратом, определяемым вторым уравнением Лагранжа:

(2.21)

Здесь - перемещение (угол поворота по каждой изi степеней подвижности);

- скорость перемещения (угловая скорость по каждой координате перемещения);

- внешние силы, действующие по каждой степени подвижности.

- функция Лагранжа, разность кинетической и потенциальных энергий данной механической системы.

Рассмотрим описание двухмассовой механической системы с упругим звеном на основе уравнения (2.21):

Поскольку система обладает двумя степенями подвижности, то получим на основе (2.21) два уравнения.

Частные производные от функции L по скоростям ибудут:

Соответственно, производные по времени от этих величин будут.

Частные производные от функции L по углу ибудут:

Подставляя найденные производные в (2.21), получим два дифференциальных уравнения, описывающих движение двухмассовой системы.

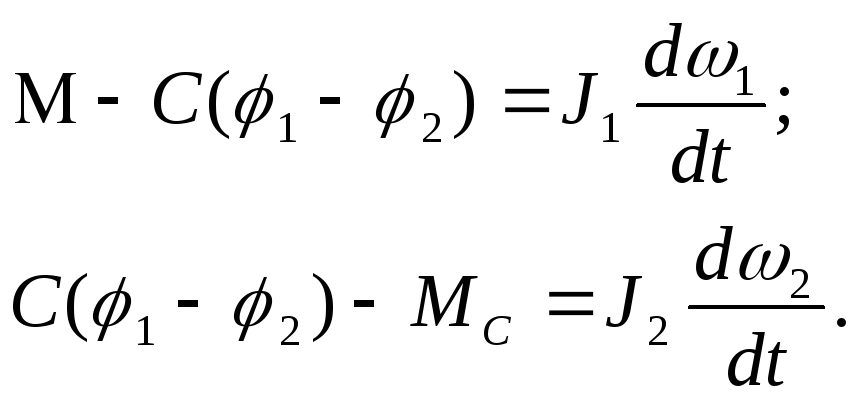(2.22)

Здесь - момент в упругом звене.

Физический смысл уравнений (2.22) уясняется из рассмотрения рис.2.9. Момент на валу двигателя М прикладывается к левому концу упругого элемента, вызывая его закручивание, что определяет появление упругого момента М_у. Разность моментов прикладывается к первой массеJ₁, определяя изменение скорости ее движения. Таким образом, первое из уравнений (2.22) – это уравнение движения электропривода для первой массы.

На втором конце упругого звена, стремящимся раскрутиться, создается момент М_у, который является движущим моментом для второй массы – рабочего органа машины. Этому моменту препятствует момент сопротивления движению М_С, прикладываемый к рабочему органу.

Разность моментов определяет изменение скорости второй массы. Второе из уравнений (2.22) есть уравнение движения электропривода для второй массы.

Решая совместно уравнения (2.22) и учитывая, что

и - угол закручивания, найдем:

(2.23)

Левая часть этого уравнения представляет собой уравнение идеального колебательного звена которое имеет период собственных колебанийи частоту собственных колебаний

(2.24)

Решение уравнения (2.23) - переходная функция двухмассового механического звена с упругостью – будет:

Т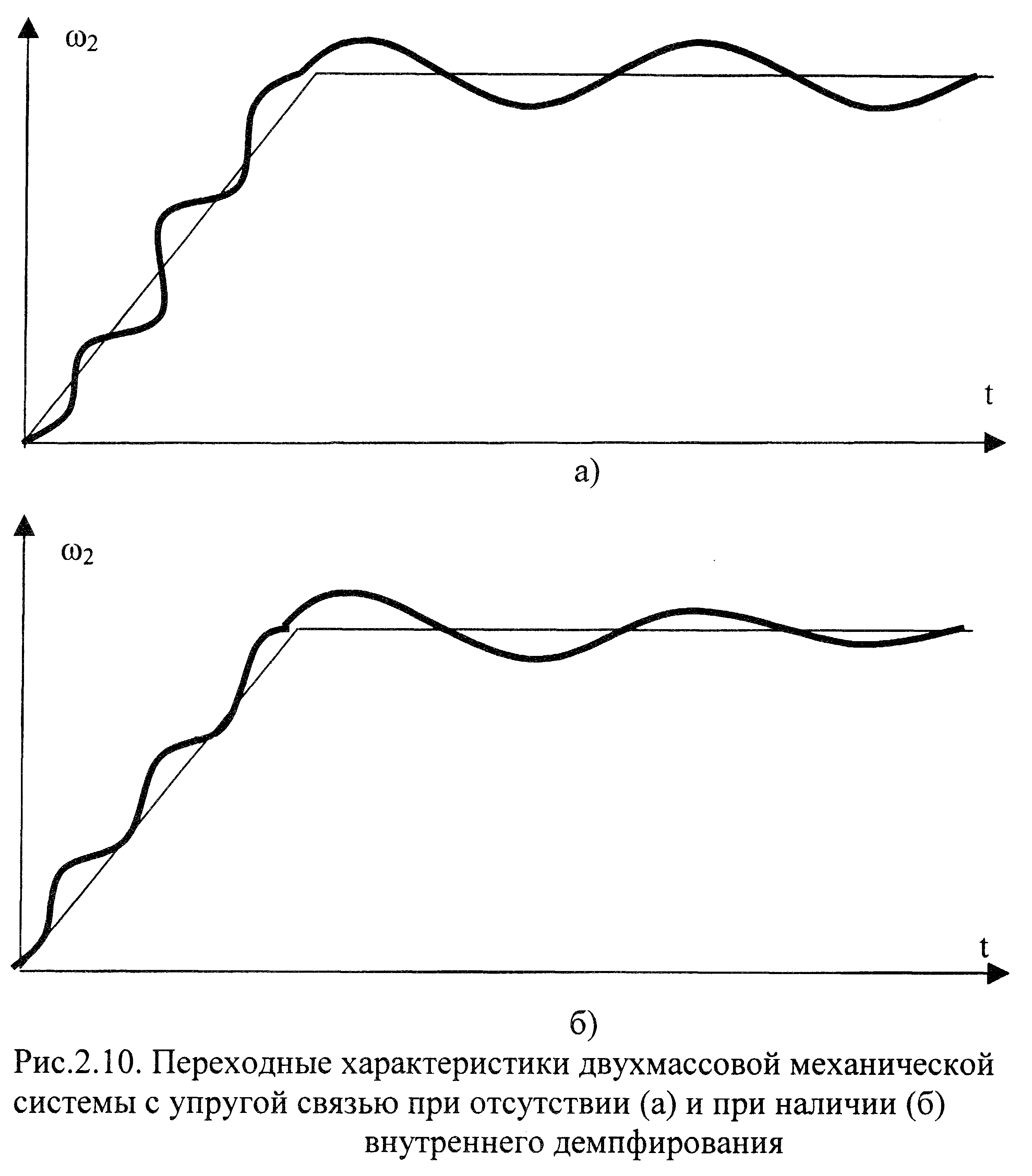аким образом, в первом приближении если мы не учитываем внутренние потери энергии (на вязкое трение, упругую деформацию), то двухмассовая механическая система, как объект регулирования представляет собой колебательное звено. Это означает, что если мы приложим к системе постоянный момент (например, при пуске двигателя), то механическая система будет иметь незатухающие колебания скорости около некоторого ее значения, определяемого средним ускорением(см.рис.2.10а).

Энергетически колебательность рассмотренной механической системы связана с тем, что периодически кинетическая энергии вращающихся масс переходит в потенциальную энергию, запасаемую в упругом элементе.

На основе уравнений (2.22), выразив их в операторной форме, можно составить структурную схему двухмассовой механической системы с упругим звеном (см.рис.2.11а). При составлении схемы учтем, что упругий момент равен .

Для того, чтобы получить передаточную функцию двухмассовой системы как объекта регулирования проведем преобразование структурной схемы, как показано на рис. 2.11б,в. Отсюда следует

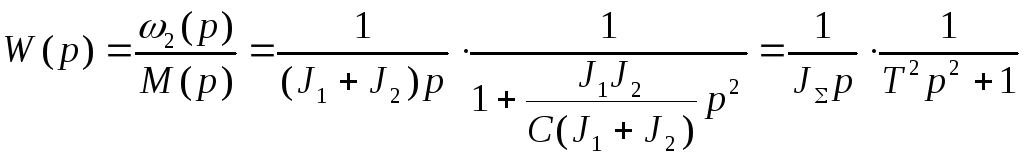. (2.25)

Таким образом, двухмассовая механическая система при отсутствии внутренних потерь (внутреннего демпфирования) может быть интерпретирована двумя последовательно соединенными динамическими звеньями: интегрирующим и колебательным. Переходная характеристика такой системы была показана на рис.2.10а.

Заметим, что, если жесткость С упругого звена достаточно велика, то механическая система может считаться жесткой и приводится к одномассовому механическому звену. При возрастании С второй член выражения (2.25) стремится к единице.

Важный практический вывод из анализа динамических свойств двухмассовой механической системы состоит в следующем. Если в составе момента двигателя или в составе статического моментаприсутствует периодическая составляющая с частотой, близкой к частотесобственных колебаний механической системы, то в системе возникают колебания с возрастающей амплитудой (явление резонанса), что может нарушить работу механизма и привести к его поломке.

Поэтому при конструировании электромеханических систем, склонных к колебаниям, необходимо определить собственную частоту колебаний механической системы и проанализировать, могут ли со стороны привода (моментМ) или механизма (момент М_С) возникнуть колебания с частотой, близкой к . В случае такого совпадения нужно развести частоты – изменить значение частоты собственных колебаний механической системы путем изменения соотношения моментов инерцииJ₁ и J₂.

В реальных механических системах всегда присутствует внутреннее демпфирование, определяемое вязким трением и потерями при деформации упругого элемента [2]. Момент сил вязкого трения пропорционален скорости. С учетом этих сил уравнения (2.22) примут вид.

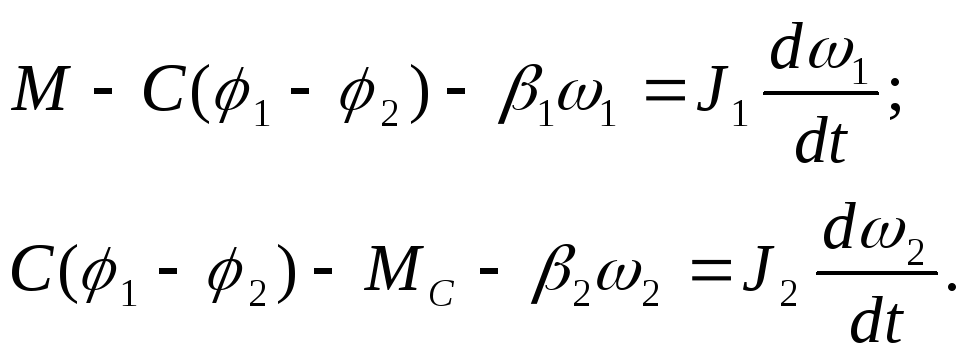(2.30)

где: - коэффициенты вязкого трения на соответствующих валах.

При учете вязкого трения колебания в двухмассовой механической системе будут носить затухающий характер (см. рис.2.10б).

В общем виде [1-2] механическая часть электромеханической системы представляет собой многомассовую систему с упругими звеньями и нелинейностями, обусловленными наличием зазоров и сухого трения. Чаще всего при анализе механических систем нет необходимости в полном учете всех факторов. В тех же случаях, особенно в прецизионных системах, когда необходим полный учет нелинейностей системы и внутреннего демпфирования целесообразно использовать математическое моделирование механической системы на ЭВМ.