3. Контрольные вопросы

1. Ориентированное и неориентированное дерево.

2. Части дерева и их свойства.

3. Примеры ситуаций, в которых необходимо построить минимальное остовное дерево.

4. Алгоритм Краскала.

4. Задания для самостоятельного решения

1. Написать программу, реализующую алгоритм Краскала.

2. Используя алгоритм Краскала, построить минмальное остовное дерево:

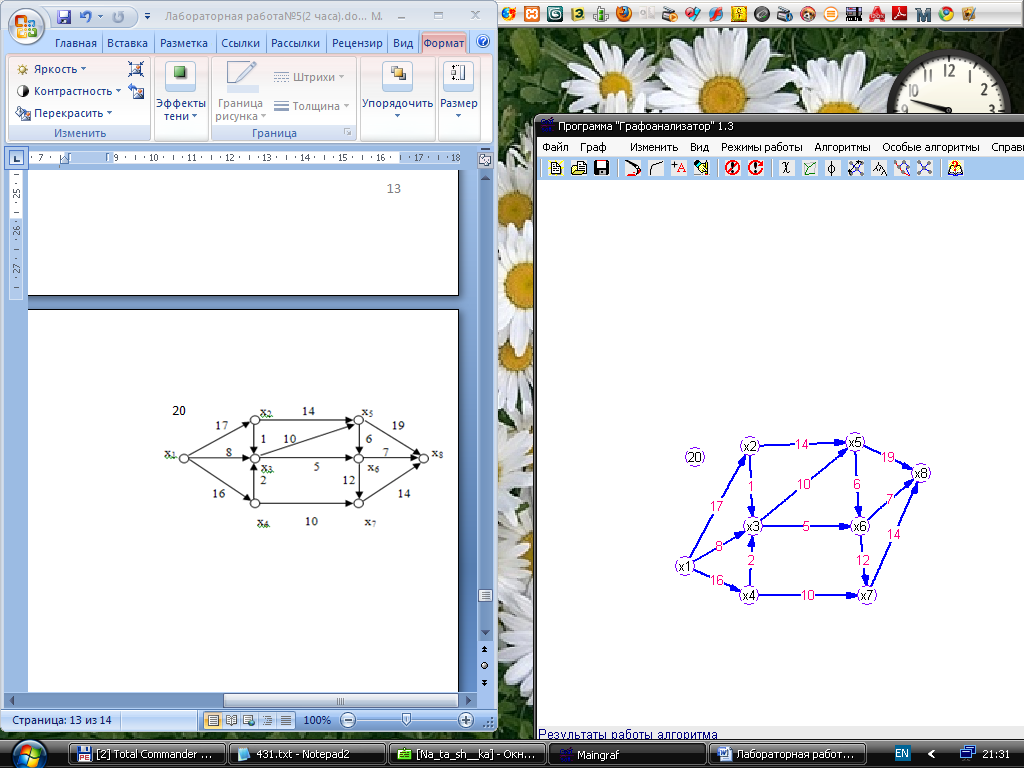
Лабораторная работа №6

Тема лабораторной работы: Нахождение кратчайшего пути. Алгоритм Дейкстры, алгоритм Форда - Беллмана.

Цели лабораторной работы:

• изучить задачу нахождения кратчайшего пути на практических примерах;

• изучить алгоритм Дейкстры и алгоритм Форда – Беллмана;

• написать программу, используя изученные алгоритмы;

• закрепить практические навыки программирования.

1. Теоретический раздел

Задача о нахождении кратчайшего пути состоит в нахождении кратчайшего пути от заданной начальной вершины до заданной конечной вершины, при условии, что такой путь существует.

Можно дать много практических интерпретаций задачи о кратчайших путях. Например, вершины могут соответствовать городам и каждая дуга - некоторому пути, длина которого представлена весом дуги. Мы ищем кратчайшие пути между городами. Вес дуги может соответствовать стоимости (или времени) передачи информации между вершинами. В этом случае мы ищем самый дешевый (или самый скорый).

Мы рассмотрим головоломку о трех бидонах.

Восьмилитровый бидон заполнен некой жидкостью, а два бидона емкостью 5 и 3 литра пусты. Необходимо разделить 8 литров жидкости на две равные части, используя только три имеющихся бидона. Какое минимальное количество переливаний из бидона в бидон надо сделать, чтобы достичь желаемого результата?

В этой сетевой модели каждый узел будет соответствовать объемам жидкости в 8-, 5- и 3-литровом бидонах. Начальным узлом будет (8, 0, 0), а конечным - (4, 4, 0). Новый узел получается из текущего при однократном переливании жидкости из одного бидона в другой.

На рис. 7 показаны различные маршруты, ведущие от начального узла (8, 0, 0) к конечному (4, 4, 0). Таким образом, наша головоломка сведена к задаче определения кратчайшего пути между узлами (8, 0, 0) и (4, 4, 0).

Рис. 7. Головоломка о трех бидонах как задача вычисления кратчайшего пути.

Оптимальное решение, показанное в нижней части рис. 7, требует семи переливаний из бидона в бидон.

2. Описание алгоритмов нахождения кратчайшего пути

2.1. Алгоритм Дейкстры нахождения минимального пути

Для нахождения минимального пути между двумя произвольными вершинами для случая, когда все с_ij > О можно воспользоваться простым алгоритмом Дейкстры

Алгоритм Дейкстры.

Шаг 1. Установка начальных условий.

Ввести число вершин графа n и матрицу весов С = (с_ij). Ввести номер начальной вер­шины s и номер конечной вершины f.

Для начальной вершины s положить M(s) = О и считать эту пометку постоянной. По­ложить M(x_i) для всех остальных вершин х_i≠ s равными достаточно большому числу (на­пример, 99999999) и считать эти пометки временными. Положить номер текущей вершины р = s. Сформировать множество П вершин с постоянной пометкой, вначале П= {р}, и множе­ство В вершин с временной пометкой, В ={Х\П}.

Шаг 2. Обновление пометок.

Заполнить множество вершин G(p), являющихся образом вершины р. Для всех вершин x_i G(p), имеющих временные пометки, т.е. для , изменить пометки сле­дующим образом:

М(х_i) - min (М(х_i), М(р)+с(р,х_i)).

Шаг 3. Превращение временных пометок в постоянные.

Из всех вершин, имеющих временные пометки, найти такую, для которой M(x*) = min(M(x_i)).

Считать пометку вершины х* постоянной. Положить р = х*.

Шаг 4. Проверка, является ли найденный путь минимальным.

Если р =f, то М(р) является длиной минимального пути; перейти к шагу 6. Иначе пе­рейти к шагу 5.

Шаг 5. Изменение множеств П и В.

Удалить номер вершины р из множества В и добавить номер вершины р в множество П. Перейти к шагу 2.

Шаг 6. Восстановление минимального пути.

Для любой вершины х_i, предшествующая ей вершина x_j определяется из соотношения:

M(x_j)+c(x_j,x_i)=M(x_i), х_j G^-1(x_i) ∩ П,

где G^-1(x_i) - прообраз вершины x_i.

Последовательно применяя это соотношение, начиная от последней вершины f, найдем минимальный путь.

Пример нахождения кратчайшего пути с помощью алгоритма Дейкстры.

Определим минимальный путь из вершины х₁ а вершину х₆ в нагруженном графе, изо­браженном на рис. 8.

Рис. 8

Рассмотрим подробно работу алгоритма Дейкстры для этого примера.

Шаг 1. Установка начальных условий.

Матрица весов имеет вид:

s=x₁; M(s)=0; p= x₁; П={ x₁}; В={ x₂, x₃, x₄, x₅, x₆}.

1-ая итерация.

Шаг 2. G(x₁)={x₂}; G(x₁)∩B={x₂}; M(x₂)=min{∞,0+1}=1.

Шаг 3. x*= x₂ ; p= x₂.

Шаг 4. x₂≠ x₆

Шаг 5. П={x₁,x₂};B={x₃,x₄,x₅,x₆}.

2-ая итерация.

Шаг 2. G(x₂)={x₃,x₄,x₆};G(x₂)∩B={x₃,x₄,x₆};M(x₃)=min{∞,1+5}=6;

M(x₄)=min{∞,1+2}=3; M(x₆)=min{∞,1+7}=8.

Шаг 3. x*= x₄; p=x₄.

Шаг 4. x₂≠ x₆

Шаг 5. П={x₁,x₂,x₄};B={x₃,x₅,x₆}.

3-ая итерация.

Шаг 2. G(x₄)={x₁,x₃,x₅};G(x₄)∩B={x₃,x₅};

M(x₃)=min{6,3+1}=4; M(x₅)=min{∞,3+4}=7.

Шаг 3. x*= x₃; p= x₃.

Шаг 4. x₃≠ x₆

Шаг 5. П={x₁,x₂,x₄,x₃};B={x₅, x₆}. 4-ая итерация.

Шаг 2. G(x₃)={x₆}; G(x₃)∩B={x₆}; M(x₆)=min{8,4+1}=5.

Шаг 3. x*= x₆; p= x₆.

Шаг 4. x₆ = x₆.

Переходим к шагу 6.

Прежде, чем перейти к восстановлению минимального пути, представим полученные результаты в виде таблицы, которой удобно пользоваться для расчетов (табл.1.)

Таблица 1.Восстановление минимального пути.

№ итерации	p	П	М(П)	В	М(В) старые	М(В) обновленные
0	1	1	0	2	∞	1
				3	∞	∞
				4	∞	∞
				5	∞	∞
				6	∞	∞
1	2	1	0	3	∞	6
		2	1	4	∞	3
				5	∞	∞
				6	∞	8
2	4	1	0	3	6	4
		2	1	5	∞	7
		4	3	6	8	8
3	3	1	9	5	7	7
		2	1	6	8	5
		4	3
		3	4
4	6

Шаг 6. Определим вершину, предшествующую вершине х₆

G^-1(x₆) ={x₂,x₃};

G^-1(x₆) ∩ П={x₂,x₃};

M(x₂) + c(x₂,x₆) =1+7≠M(x₆),

M(x₃) + c(x₃,x₆) = 4+1=5=M(x₆),

т.е. вершина x₃ предшествует вершине x₆.

Определим вершину, предшествующую вершине х₃

G^-1(x₃) ={x₂,x₄};

G^-1(x₃) ∩ П={x₂,x₄};

M(x₂) + c(x₂,x₃) =1+5≠M(x₃),

M(x₄) + c(x₄,x₃) = 3+1=4=M(x₃),

т.е. вершина x₄ предшествует вершине x₃.

Определим вершину, предшествующую вершине х₆

G^-1(x₄) ={x₂};

G^-1(x₄) ∩ П={x₂};

M(x₂) + c(x₂,x₄) =1+2=3=M(x₄),

т.е. вершина x₃ предшествует вершине x₃.

Определим вершину, предшествующую вершине х₂

G^-1(x₂) ={x₁};

G^-1(x₂) ∩ П={x₁};

M(x₁) + c(x₁,x₂) =0+1=1=M(x₂),

т.е. вершина x₁ предшествует вершине x₂.

Итак, x₁ x₂ x₄ х₃ x₆ есть минимальный путь из вершины х₁ в вершину х_6. Его длина равна 5.