ГОС / 6

6. Момент импульса системы частиц. Закон сохранения момента импульса и его связь с изотропностью пространства.

Пусть О - какая-либо неподвижная точка в инерциальной системе отсчета. Ее обычно называют началом или полюсом. Обозначим через радиус-вектор, проведенный из этой точки к точке приложения силы (рис. 1) .

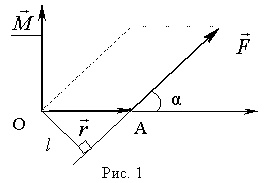Моментом силы относительно точки О называется векторное произведение радиус-вектора на силу : , , (1) - угол между векторами и ; направление выбирается так, чтобы последовательность векторов , , образовывала правовинтовую систему, т. е. если смотреть с конца вектора , то поворот по кратчайшему пути от первого сомножителя в (1) ко второму осуществляется против часовой стрелке, таким образом совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от к по наикратчайшему пути.

Моментом нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки (2)

Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора на импульс : (3)

Для системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала: 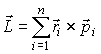. (4) Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем .

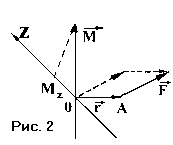При неподвижной точке О вектор , равный , параллелен и поэтому . Кроме того . Таким образом (5)

Это уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая под М момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что где - сила воздействия k-й материальной точки на i-ю. Кроме того, эти силы и , действуют вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате опять получается уравнение моментов типа (5) только для системы материальных точек, в котором определяется выражением (4), а - выражением (2) для внешних сил, т. е.

. (6)

Моментом силы механической системы относительно оси называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рис. 2). Соответственно, моментом импульса относительно оси называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси.

Можно доказать, что выбор точки на оси влияет на значения моментов импульса и относительно точки, но не влияет на значения соответствующих проекций моментов на эту ось. Если мы выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то имеем: (7)

Если система замкнута (т. е. внешних сил нет), то и, следовательно, согласно уравнению (6) вектор не изменяется со временем, т.е. . Отсюда вытекает закон сохранения момента импульса, который гласит, что

МОМЕНТ ИМПУЛЬСА ЗАМКНУТОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК ОСТАЕТСЯ ПОСТОЯННЫМ.

Момент импульса сохраняется и для незамкнутой системы, если сумма моментов внешних сил равна нулю. Момент импульса сохраняется во внешнем центрально-симметричном поле. Наряду с законом сохранения импульса и энергии закон сохранения момента импульса является одним из фундаментальных законов физики. Такой расширенный закон сохранения момента импульса уже не является теоремой механики, а должен рассматриваться как самостоятельный общефизический принцип.

Вывод закона сохранения момента импульса.

L – момент импульса . Здесь - радиус вектор i-ой точки, и соответственно ее масса и импульс.

Примечание. К сожалению, функция Лагранжа и момент импульса обычно обозначаются одной буквой L. Можно доказать закон сохранения импульса через изотропность пространства. Изотропность пространства означает, что если замкнутую систему повернуть на любой угол в пространстве, то это не повлияет на свойства системы.

Функция Лагранжа – функция, которая определяет состояние системы в данный момент времени. Она определяется по формуле , где T – кинетическая энергия системы, U – потенциальная. Функция Лагранжа зависит от обобщенных координат, обобщенных скоростей и времени.

Докажем закон сохранения момента импульса. Выберем обобщенную координату таким образом, чтобы ее изменение характеризовало поворот рассматриваемой системы, как целого в данном направлении. Примером такой координаты может служить угол в цилиндрической системе координат или угол Эйлера. Пространство изотропно, поэтому, если система замкнута, то ее поворот в целом на угол вокруг любой из осей (на рисунке приведена ось OZ) не влияет на состояние системы, тогда: . Запишем уравнение Лагранжа для координаты. . Отсюда (8).

Рассмотрим физический смысл этой величины . В классической механике потенциальная энергия от угловой скорости не зависит, поэтому . Отсюда . Поэтому 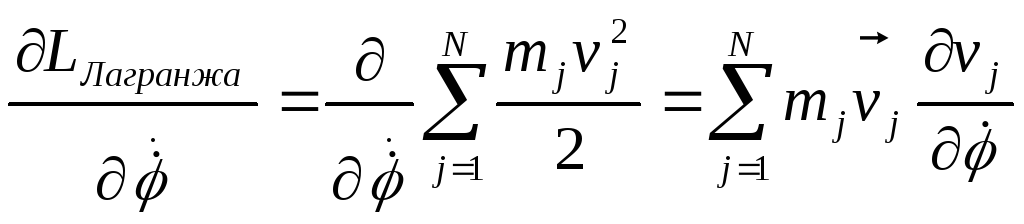(9),

j – номер материальной точки, входящей в систему , - скорость j-ой точки, - ее масса. Это выражение можно получить, используя правило вычисления производной функции, заданной параметрически. Вычислим , используя определение производной . Здесь величина переноса всей системы в целом вдоль оси х.

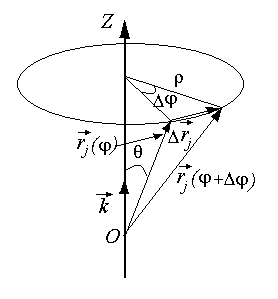Из рисунка видно, что . Учитывая направления, получим , где единичный вектор вдоль оси поворота OZ. Поэтому . Подставив полученное выражение в (9) получим 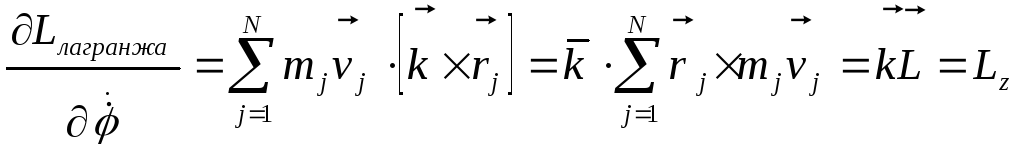. Здесь - вектор общего момента импульса системы, - его проекция на ось z. Согласно формулы (8) сохраняется в замкнутой системе. Если при доказательстве в качестве обобщенной выбрать не координату z, а координату х или у, то получим . Поэтому в целом общий момент импульса системы , что и требовалось доказать. Так как при доказательстве этого закона пользовались одним постулатом изотропности пространства, то закон сохранения момента импульса является следствием изотропности пространства.

3