Ovru-all

3.4. Чисельні розв’язки задач тепло- й масоперенесення

3.4.1.Різницеві схеми розв’язку задач тепло- й масоперенесення

Застосування ЕОМ для розв’язку задач тепло- й масоперенесення, у тому числі і для вирішення крайових задач росту кристалів, виявилося дуже ефективним. Література з цього питання обширна. Питанням вибору звичайно-різницевих схем для вирішення завдань теплопровідності присвячені книги [10-12]. Побудуємо для задачі Коші

∂u −	∂u = ϕ(x,t),	− ∞ < x < ∞, 0 < t < T,	(3.65)
∂t	∂x	,

u(x,0) = ψ(x)

одну із можливих різницевих схем, що її апроксимують. У якості сітки використовуємо сукупність точок перетину прямих:

x=mh, t=nτ, m=0, ±1, …….; n=0,1, …… ,[T/τ],

[T/τ] – ціла частина дробу [T/τ]. Вважатимемо, що крок значень часу τ пов'язаний з кроком h залежністю τ=rh, так що сітка Dh залежить тільки від одного параметра h. Шуканою сітковою функцією є таблиця [u]h=[u(mh,nτ)] значень розв’язку задачі (3.65) u(x,t) в точках сітки Dh.

Перейдемо до побудови різницевої схеми, що апроксимує завдання (3.65). Значення сіткової функції uh в точці сітки (xm,tn)= (mh,nτ)

позначатимемо unm. Замінимо похідні (дu/дt) і (дu/дx) різницевими відносинами:

(дu/дt)x,t ≈	u(x,t + τ) − u(x,t)	,	(дu/дx)x,t ≈	u(x + h,t) − u(x,t)	,
	τ
				h

а в початковий момент часу t=0 значення u0m визначаються крайовою умовою u(x,0)= ψ(x).

Шукатимемо сіткову функцію u(h)= unm = u(mh,nτ). Таке завдання

записують в загальному вигляді таким чином:
Lhu(h) = f (h) ,	(3.66)

де Lh – диференціальний оператор (3.65) для сіткової функції; f(h) – це пара сіткових функцій, одна з яких задана на двовимірній сітці

	un+1	− un		un	− un
	m	m	−	m+1	m	= ϕ(mh,nτ),	(3.67)
		τ		h
а інша – на одновимірній:				u0m=ψ(mh).
							101

Різницеве рівняння (3.67) можна розв’язати відносно un+1m, отри-

мавши
un+1m=(1–r) unm +r unm+1 +τϕ(mh,nτ).	(3.68)

Отже, знаючи значення unm, у точках сітки m=0, ±1,….., при t=nτ, можна обчислити значення un+1m у точках сітки при t=(n+1)τ. Оскільки значення u0m при t=0 задані рівністю u0m=ψ(mh), ми можемо крок за кроком обчислити значення розв’язку u(h) у точках сітки на прямих t=τ, t=2τ, тобто усюди на Dh.

Апроксимація

Різницева задача (3.66) апроксимує (3.65), якщо в рівності

Lh [u]h = f(h) + δf(h)

(3.69)

нев'язність δf(h) , що виникає при підстановці сіткової функції [u]h в різницеву крайову задачу (3.65) прямує до нуля при h→0. Припустимо, що рішення задачі (3.65) має обмежені другі похідні і скористаємося формулою Тейлора

u(xm + h,tn ) − u(xm ,tn )		=	∂u(xm ,tn )	+		h ∂2u(xm + ξ,tm )
			∂x					∂x2	,
h					2
u(xm ,tn + τ) − u(xm ,tn )		=	∂u(xm ,tn )	+		τ ∂2u(xm ,tm			+ η)
			∂t					∂τ2	,
τ					2

де ξ і η – деякі числа, залежні від m, n і h, що задовольняють нерів-

ностям 0<ξ<h, 0<η<τ. Тоді не важко переконатися (див. [16]), що нев'язність

δf (h) =		τ		∂2u(xm ,tm + η)		−	h	∂2u(xm + ξ,tm ) .
2					∂t2	2				∂x2
Отже,					∂2u(x,t)|+ sup|					∂2u(x,t)|)h .
|δf (h) |≤ (	r		sup|						1		(3.70)
2					∂t2	2				∂x2

Таким чином, розглянута різницева схема має перший порядок апроксимації відносно h на розв’язку u(x,t), якщо шукана функція має обмежені другі похідні.

Збіжність та стійкість. Різницева крайова задача (3.65) за визначенням стійка, якщо існують числа δ>0 і h0>0 такі, що при будьякому h<h0 і будь-якому δf(h) з F, що задовольняє нерівності

102

||δf(h)||F ≤δ, різницева крайова задача (3.65) має один і лише один розв’язок z(h), причому виконується умова

|| z(h) – u (h) ||U≤C||δf(h)||F,

(3.71)

де С – деяка стала, не залежна від h. Властивість стійкості можна трактувати як рівномірну відносно h чутливість розв’язку різницевої крайової задачі (3.66) до збурень f(h) у правій частині (3.69).

У разі лінійного оператора Lh сформульоване визначення рівносильне наступному:

Різницева крайова задача (3.66) стійка, якщо існує h0 >0 таке, що при h<h0 і будь-якому f(h) вона однозначно вирішувана, причому

|| u (h) ||U≤C||f(h)||F,

(3.72)

де С – деяка стала, не залежна від h і f(h).

Різницева схема (3.67) стійка при r<1 [12]. У випадку r>1 різницева схема (3.67) як і раніше апроксимує задачу (3.65), але в цьому випадку немає збіжності розв’язку u(h) до розв’язку u(x,t) диференціальної задачі (3.65).

У разі рівнянь з частинними похідними непридатність навмання взятої апроксимуючої різницевої схеми є правилом, а вибір стійкої (і, отже, збіжної) різницевої схеми - постійною турботою обчислювача.

Явні та неявні різницеві схеми.

Приведемо дві різницеві схеми, що апроксимують задачу Коші для рівняння теплопровідності:

	∂u −		∂2u = ϕ(x,t),			− ∞ < x < ∞, 0 < t < T,
	∂t		∂x2				(3.73)
	u(x,0) = ψ(x)
Найпростіша з них
		un+1 − un			un	− 2un	+ un
L(1)u(h) ≡		m	m	−	m+1	m	m−1	= ϕ(mh,nτ)
						h2
h			τ
при –∞<x<∞, 0<t <T							(3.74)
um0 = ψ(mh)			– ∞ <x<∞

одержується при заміні похідних різницевими співвідношеннями, в які входять значення сіткової функції на попередньому часовому проміжку.

Якщо для заміни другої похідної брати значення функції вже в наступний момент часу, прийдемо до іншої схеми

103

	un+1	− un			un+1	− 2un+1	+ un+1
L(2)u(h) ≡	m	m		−	m+1	m	m−1	= ϕ(mh,nτ)
		τ				h2
h
при – ∞<x<∞, 0<t<T							(3.75)
um0 = ψ(mh)		– ∞<x<∞.

Ці схеми істотно відрізняються. Обчислення рішення u (h) по першій з них не додає труднощів і проводиться по явній формулі

un+1m=(1–2r) unm +r (unm + unm+1) +τϕ(mh,nτ)

(3.76)

послідовно на кожному новому часовому шарі.

Друга схема позбавлена такої зручності. Оскільки в рівняння (3.75) входить багато значень сіткової функції на наступному часовому шарі, потрібно складати і розв’язувати системи алгебраїчних рівнянь. Проте, свого часу схему (3.75) застосовували дуже широко,

оскільки вона є стійкою при r >1. При τ =rh2, r =const обидві схеми мають другий порядок апроксимації відносно h, нев'язка ||δf(h)||F == O(h2) [12].

У випадку не дуже дрібних сіток (з порівняно невеликим числом вузлів) друга схема дає економію машинного часу за рахунок засто-

сування великого кроку τ за часом. З фізичної точки зору сітки повинні бути дрібними в області великих змінних градієнтів температури або концентрації і ділянок поверхні з великою кривизною. У разі ж рухомих поверхонь розділу фаз крок за часом, як правило, повинен бути істотно менше, ніж це визначається умовами стійкості для нерухомих меж.

Для розв’язку крайових задач тепло- і масоперенесення (рівняння з частинними похідними) застосовують різні сітки із змінним кроком по координатах і різні способи апроксимації. Аналіз збіжності в цих випадках, як правило, дуже ускладнений. Про якість вживаних схем судять за згодою з аналітичними розв’язками для окремих випадків із спрощеними граничними умовами або по здатності методу описати відомі фізичні явища і передбачити нові. Якщо є можливість, проводять складні експерименти з визначення теплових полів, фізичного моделювання течій в розплаві і порівнюють числові розв’язки з експериментальними даними. У разі збігу результатів з'являються підстави застосовувати спосіб апроксимації для подібних задач.

104

3.4.2. Проблема крайової умови на міжфазній межі при рості кристалів

Гранична умова типу (3.39) або (3.49) балансу тепла або речовини на міжфазній межі в загальному випадку двовимірних або тривимірних задач істотно ускладнює використання числових методів. При прямому їх обліку шляхом запису відповідних виразів в кінцевих різницях стійкий рахунок зазвичай отримати не вдається із-за некоректного завдання початкових умов. Це пов'язано з тим, що в крайову умову, що зв'язує швидкість росту з потоками, не входить інтервал часу. Тому в 60-70-х роках великого поширення набули однорідні різницеві схеми [13-16] з "розмазанням" теплоємності по температурі. У них теплота кристалізації враховується введенням для області, прилеглої до фронту кристалізації, деякої ефективної теплоємності. При цьому використовувалися переважно неявні схеми [16]. Такий підхід відноситься до так званих методів фазового поля, коли задача тепло- й масоперенесення розв’язується для якби однієї фази, а положення міжфазної границі визначається значенням деякого параметра, наприклад, температури плавлення.

Для розв’язку задач Стефана, що описують кристалізацію (плавлення) різних матеріалів, як правило, використовуються дві групи методів чисельного рішення задачі [17]. Перша група методів використовує узагальнений, або ентальпійний, запис прихованої теплоти кристалізації (плавлення) в самому рівнянні – метод фазового поля [16]. Це призводить до необхідності тієї або іншої апроксимації нелінійних членів в рівнянні або, іншими словами, до «розмазання» прихованої теплоти. Ці методи добре пристосовані до знаходження узагальненого розв’язку задачі Стефана, зокрема для опису двофазної зони (області, зайнятою і твердою, і рідкою фазами), якщо вона виникає. Друга група методів виходить з класичної постановки задачі Стефана і приводить до необхідності виділення фронту кристалізації тим або іншим способом [5, 6]. Обидві групи методів мають самостійне значення і повинні розвиватися незалежно, оскільки є випадки, коли розв’язок задачі в узагальненій постановці не співпадає з класичним розв’язком [17].

Таким чином, кожен з вказаних двох підходів чисельного розв'язку може дати якісно різні рішення задачі. Наприклад, перша група методів в принципі не може дати чисельного розв'язку з переохолодженням в розплаві і, навпаки, при другому підході не можна отримати розв'язки за наявності двофазної області.

105

У [15] розглянуті різні способи апроксимації нелінійних членів рівняння в узагальненій постановці задачі. Аналізувалася можливість отримання достатньо точного чисельного розв’язку задачі у випадку гладкого класичного фронту кристалізації. Аналіз проводився на модельній задачі кристалізації довгого циліндрового зразка при великих швидкостях кристалізації, коли фронт кристалізації має достатньо складну форму. Результати числових розрахунків різними методами порівнювалися з аналітичним розв’язком модельної задачі

водновимірному наближенні.

3.4.3.Перші числові розв’язки дифузійних задач росту кристалів

Числові розв’язки задачі про зростання включень β-фази в матри-

ці α- фази для випадків плоскої, циліндрової і сферичної поверхонь розділу фаз проведено в [18]. Автори використовували метод розв'я- зку в кінцевих різницях залежного від часу рівняння дифузії. Ними встановлено, що для отримання розв’язків високої точності необхідно вибирати достатньо малі інтервали по відстанях, на які розбивається кінцевий об'єм розчину. Інтервал за часом так само повинен бути порівняно малий – його величина повинна задовольняти умові

t≤Δx2/(2D)

(3.77)

( x – інтервал за відстанню, D – коефіцієнт дифузії). Малі інтервали за часом і відстані вимагають значних витрат машинного часу у випадку, якщо об'єм розчину не є малим. А задачі росту кристала з великого і малого об'ємів істотно розрізняються за результатами, оскільки в останньому випадку, помітно знижується середня концентрація розчину під час росту.

У [13] для розв’язку задачі з циліндровою симетрією на прямокутній сітці (межа коло) рівняння (3.37) записувалося у вигляді

c(U) (дU/дx)=div(κ(U) grad(U)) +f, (3.78)

f – потужність теплових джерел; U≡Т ; с(U)= cρρ.

Межа розділу визначається умовою, що U(r,t)=U*. З цього знаходять положення межі R(t). У загальному випадку рівняння для межі розділу має вигляд Ф(U(r,t))= Ф(r,t)= 0, grad(Ф) перпендикулярний

поверхні розділу фаз, і умову (3.39) можна записати так:
[κgradU1-κgradU2] gradФ+λ(дФ/дt)=0	(3.79)
(індекси 1,2 відносяться до різних фаз).

106

При U=U* питома об'ємна енергія w потерпає стрибок λ (ентальпія кристалізації)

U

w= ∫ c(U)dU +λη(U–U*);

0

c1(U) при U<U*

c(U)=

c2(U) при U>U*

U–U*=ξ; η(ξ)=1 при ξ>0; η(ξ)=0 при ξ<0.

Враховуючи, (3.78) у вигляді dw(ξ,t)/dt=div(κgradU)+f і умову dU(ξ,t)/dξ=δ(T) (дельта функція), можна записати:

[c(U)+λδ(U–U*)](дU/дt)=div(κ grad(U)) +f,

(3.80)

Причому рівняння (3.80) включає (3.78) і умову балансу тепла на межі (3.79).

Згладжування коефіцієнта [c(U)+λδ(U–U*)] полягає в заміні на інтервалі [U*– , U*+ )] розривної функції η(U– U*) безперервною функцією η(U–U*, ) такою, що η′(ξ, )=δ(ξ, ). Отже, вводиться згла-

джування або ефективна теплоємність сеф(U)=с(U)+λδ(U–U*, ) з умов

сеф(U)=с(U) поза інтервалом [U*–		, U*+	)]
U* +	U*	U* +
і ∫ сеф(U)dU = l +	∫ с1(U)dU	+ ∫	с2 (U)dU .
U* −	U* −	U*

Тепер рівняння (3.80) апроксимується однорідною різницевою схемою, придатною для наскрізного рахунку. Описана тут задача вирішувалася в [11] методом, що полягає в поетапному розв'язку для різних просторових змінних (х,у) одновимірних рівнянь теплопровідності за допомогою безумовних стійких неявних схем [2,13] .

3.4.4. Спосіб чисельного розв'язку задачі росту або розчинення кулястого або циліндрового кристала

В [18] автори враховували рух міжфазної межі, але концентрація на ній приймалася постійною, рівною рівноважній.

У [19] вирішувалася дифузійна задача для випадків виділення або розчинення сферичної і циліндрової частинок, причому в ряді

107

розв’язків враховувалася зміна поверхневої концентрації. Залежні від часу рівняння дифузії для сферичної або циліндрової симетрії записувалося в кінцевих різницях,

		∂2Сi-1		K ∂Сi-1
Сi	= D t	n	+		n	+ C′,	(3.81)
n		∂r2		r ∂r

де Сni – зміна концентрації в n-й точці за i-й проміжок часу, К= 1 або 2 відповідно до випадків циліндрової або сферичної симетрії.

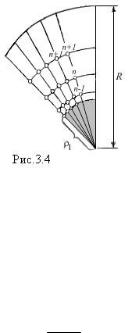
Інтервал r за відстанню між вузлами сітки вибирали не рівномірний, а такий, що зростає за арифметичною прогресією (рис.3.4);

rn= rn-1+δ, δ=2(R–ρ)/[N(N –1)], (3.82)

де ρ - радіус кристала; R - радіус кювети; N - число інтервалів, на які розбивається відрізок R−ρ. Це дозволяло апроксимувати розподіл концентрації на області, де вона швидко змінюється, великим числом дискретних значень. Далеко від кристала, де градієнти концентрації малі, згідно (3.82) задаються великі інтервали. У зв'язку із зміною радіусу частинки координати вузлів сітки на кожному кроці за часом (че-

рез інтервал t) розраховуються заново.

Після запису в кінцевих різницях похідних від концентрації:

∂Сi-1

Сi-1

− Сi-1

∂2Сi-1

Сni-+11 − Сni-1

−

Сni-1 − Сni--11

r

− r

r − r

n

=

n+1

n-1

,

n

=

n+1

n

n

n−1

,

∂r

r

− r

∂r2

0.5(r

− r

−1

)

n+1

n−1

n+1

n

а також поправки до концентрації, пов’язаної зі зміною координат всіх вузлів сітки при переміщенні міжфазної межі:

C' = ∂Сni-1 (rni − rni−1 ) можна розраховувати всі нові концентрації

∂r

послідовно у всіх вузлах сітки на кожному кроці за часом (методом прогонки).

i

i-1

∂2Сni-1

K ∂Сni-1

Сn

= Сn

+ D t

2

+

+

C′,

(3.83)

∂r

r ∂r

У разі постійної рівноважної концентрації на міжфазній межі (ріст не достатньо великого кристалика в дифузійному режимі) швидкість росту визначається виразом умови балансу речовини (3.51)

108

V(C		− С	n=1	) = D	∂C| ,		(3.84)
	К				∂r ρ
в якому похідна дС/дr записується як (Ci					− Ci	)/(ri − ρi ). Відповідно
				1	e		1

ρi = ρi−1 + Vi t .

Для виконання граничної умови, що виключає потік речовини через зовнішню межу розчину, вводиться додаткова сфера N+1, в якій концентрація не розраховується, а їй приписується значення, знайдене для N-1 сфери, доки концентрація у N-1 шарі не змінюється. Доки кристал набагато менше розміру сферичної кювети чисельний розв’язок відповідає випадку зростання з нескінченного розчину і може бути перевіреним шляхом порівняння з відповідними аналітичними рішеннями. При значній зміні концентрацій на краю кювети ми маємо випадок зростання з кінцевого об'єму розчину. Застосування нерівномірних інтервалів дозволяє на порядок зменшити число точок (шарів), для яких ведуться розрахунки, і вирішувати такі завдання при порівняно малих витратах машинного часу. При необхідності аналізу зростання кристала в широкому інтервалі розмірів можна, як це було запропоновано в [20] вибирати об'єм кювети спочатку невеликим, але ввести процедуру, що збільшує розмір кювети і що відповідно змінює координати точок і концентрації в них, як тільки концентрації в N-й точці відхилиться на задану малу величи-

ну ε від значення С∞, яке спочатку приписувалося майже всім точкам (окрім найближчих до поверхні спочатку заданого дуже малого кристала). При цьому точкам з координатою r, меншою радіусу попереднього розміру кювети приписуються концентрації, що відповідають старому розподілу, а решті всіх точок значення С=С∞.

На рис. 3.5 наведені для приклада розраховані розподіли концентрацій для випадків росту сферичної та циліндричної частинок із розчину з 80% основного компонента (С0=0.785) у порівнянні з аналітичними розв’язками рівняння Лапласа – стаціонарного розподілу для випадку незростаючої частки. Розраховані розподіли точно збігаються з аналітичними розв’язками Г.П. Іванцова для випадку постійної поверхневої концентрації [8]. Розв’язку рівняння Лапласа для нескінченного за радіусом циліндрової кюветі з розчином не існує, а для сфери такий розв’язок (крива 3) свідчить про плавний хід концентрацій на нескінченність, що не відповідає дійсності у випадку рухливої міжфазної межі.

109

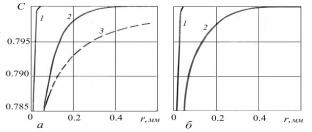
Рис. 3.5. Розподіли концентрації при рості сферичного (а) та циліндричного кристалів (б),

1 – початкові, 2 – кінцеві, 3 – згідно з рівняння Лапласа;

С∞=0.8, Сρ=0.785, = 3×10–9 м2/с.

Як свідчать розрахунки, для отримання достатньо високої точності розв’язків необхідно, щоб найменші інтервали за відстанню поблизу кристала були приблизно на порядок меншими його розміру.

Для стійкості схеми розрахунку потрібно, щоб інтервал за часом t не перевищував значення, що відповідає формулі (3.77), тобто допустимі дуже малі його значення при малому розміру кристалика. Неявні схеми розрахунків (дивись вище) залишаються стійкими при

значно більших значеннях t. Але у випадку нестаціонарних розподілів і рухливої міжфазної межі похибки з часом можуть накопичуватись, а схеми розрахунків набагато складніші.

Приведена схема чисельного розв’язку застосовна і для випадку зростання кристала з власного розплаву. В цьому випадку слід замінити концентрації температурою, коефіцієнт дифузії – коефіцієнтом температуропровідності. На міжфазній межі повинна виконуватися умова балансу тепла. Якщо розглядати температурне поле і в рідкій і в твердій фазі, то його потрібно враховувати у вигляді (3.79). Точнішим буде одночасний розв’язок теплової і дифузійної задачі. Це робити необхідно (і раціонально, за витратами машинного часу) для випадків росту з розплавів з малим змістом другого компоненту (не більше 1-2% домішки). Для випадку росту з металевого бінарного розплаву з достатньо великим змістом другого компоненту теплову задачу можна не розглядати, оскільки зростання кристала лімітується в цьому випадку не відведенням теплоти від фронту кристалізації, а дифузією.

Описана методика використовується в лабораторних роботах "Ріст сферичної частинки" та "Лазерна обробка поверхні метала", (допоміжний посібник).

110