2.6.3. Многоканальные системы массового обслуживания.

Модель 3.

Пусть параллельно могут обслуживаться не более s клиентов. Такие модели называются многоканальными (s – число каналов обслуживания). Здесь _n = (n0), _n = n при n s , _n = s при n  s. Рассмотрим случай неограниченной длины очереди.

Для данной модели расчетные формулы (Эрланга) имеют вид:

Р_n = Р₀(/)ⁿ / n (n  s), (2.6.9)

Р_n = Р₀(/)ⁿ / s/s^n-s (n  s), (2.6.10)

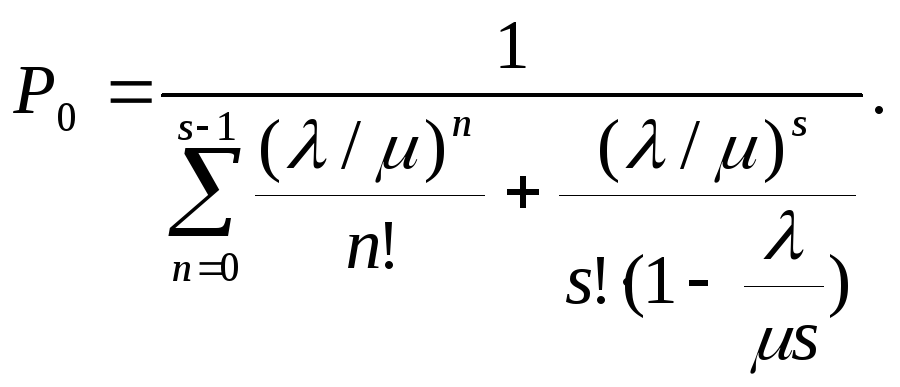(2.6.11)

Для –среднее число клиентов, ожидающих обслуживания:

= Р₀(/)^s+1/(s–1)/(s–/)², (2.6.12)

для общего числа клиентов, находящихся в системе, имеем

n = +/, (2.6.13)

для –среднее время ожидания обслуживания:

=/. (2.6.14)

Вероятность обязательного пребывания в очереди равна вероятности занятости всех каналов обслуживания. Обозначим ее через W. Тогда

W= Р₀(/)^s/s. (2.6.15)

Известный интерес представляет вероятность того, что суммарное время обслуживания и его ожидания превзойдет заданную величину t. Обозначим эту вероятность через Р(>t).

Р(>t)=e^–t(1+(W/s)(1– e^{–st(1–/s–1/s)})/(1–/s–1/s)). (2.6.16)

Вычисления в соответствии с данной моделью могут оказаться весьма громоздкими, тогда используют приближенные методы. Например, при /1 можно принять Р₀ 1 – /, (/)^s+1/s², тогда как для значений /, близких к 1,

Р₀  (s – /)(s – 1)! /s^s и  (/)/(s – /).

Пример 2.6.4. Пусть на нашей станции 3 канала обслуживания (исполнителя), а мест для ожидания неограниченное число. Пусть, как и прежде  = 5 и  =6. Имеем / =0.833, s =3 и

Р₀ = 1/(0.833⁰/0+0.833¹/1+0.833²/2!+ 0.833³ /(3!(1 –0.833/3))) = 0.432,

=0.4320.833⁴/2/(3–0.833)² = 0.022,

=0.022/5 = 0.0044 часа.(16 сек.)

Таким образом, при данных условиях 43.2% времени станция простаивает, среднее время ожидания обслуживания составляет 16сек. С точки зрения клиента отлично, но простой оборудования (исполнителей) влетает в копеечку. Кроме того, имеем:

Р₁ =0.40, Р₂ =0.15, Р₃ =0.04.

Вычислим параметры системы при 2 исполнителях.

Р₀ = 1/(0.833⁰/0+0.833¹/1+ 0.833² /(2!(1 –0.833/2))) = 0.412,

= 0.4120.833³/1/(2–0.833)² = 0.17,

= 0.17/5 = 0.034 часа.(2 мин.)

Простой составляет 41.2% времени, среднее время ожидания 2 мин.

Сравним с результатами примера 2.6.2, где при наличии только одного исполнителя простой составлял 17%, а среднее время ожидания 50 мин. В силу малого времени ожидания параметры W и Р(>t) в данном примере интереса не представляют. Р₁ =0.34, Р₂ =0.14, Р₃ =0.06.

Модель 4.

Рассмотрим теперь модель, которая отличается от предыдущей только тем, что число мест для ожидания обслуживания ограничено величиной k. Здесь _n = при 0≤n < k+s и _n =0 при n  k+s; _n = n при ns, _n = s при s ≤ n ≤ s+k.

Формулы для характеристик модели имеют вид:

Р_n = Р₀(/)ⁿ / n (n  s), (2.6.17)

Р_n = Р₀(/)ⁿ / s/s^n-s (s ≤ n ≤ s+k ), (2.6.18)

, /≠s, (2.6.19)

, /=s, (2.6.20)

Для –среднее число клиентов, ожидающих обслуживания:

=Р₀(/)^s+1(1–(/s)^k–k(/s)^k(1–/s))/(s–1)/(s–/)², /≠s, (2.6.21)

=Р₀(/)^sk(k+1)/(2s), /=s, (2.6.22)

для –среднее время ожидания обслуживания:

=//(1– Р_k+s). (2.6.23)

Пример 2.6.5. Пусть в дополнение к последнему примеру наша станция располагает двумя местами для ожидания обслуживания (k=2 и s=2). Тогда получим:

Р₀=1/(0.833⁰/0+0.833/1!+0.833²(1–(0.833/2)²⁺¹)/2!/(1–0.833/2)) = 0.423,

=0.4230.833³(1–(0.833/2)²–2(0.833/2)²(1–0.833/2))/1/(2–0.833)²=0.25,

и =0.25/5/(1– Р₂₊₂)= 0.25/5/(1 – 0.4230.833⁴ /2/2²)=0.05 час.

Для двух каналов обслуживания входной поток заказов очень слабый, изменим его, пусть =12, тогда /=2= s и мы имеем

Р₀=1/(2⁰/0 +2/1!+2²(2+1)/2!)= 0.111,

=0.111*2²*2*3/(2*2)=0.67,

=0.67/12/(1–Р₂₊₂)=0.67/12/(1–0.1112⁴/2/2²)=0.07 ч.

При таком входном потоке простой оборудования составляет 11.1%, а среднее время ожидания обслуживания 0.0760= 4.3 мин.

Рассмотрим более крупный пример, на котором нагляднее иллюстрируются формулы моделей 3 и 4.

Пример 2.6.6.

Вариант 1. Имеем станцию с 4 каналами обслуживания и с неограниченным количеством мест для ожидания. Пусть =20 заявок в час, время обслуживания одной заявки 11.5 мин. (=60/11.5=5.217), тогда /=20/5.217=3.83 и s=4. Используем (2.6.11):

Р₀= 1/(3.83⁰/0!+3.83/1!+3.83²/2+3.83³/3+3.83⁴/4/(1–3.83/4))=0.0042.

Из (2.6.12)–(2.6.14) получаем среднее время ожидания:

=0.00423.83⁵/3!/(4–3.83)²/20= 1 час.

Вероятность обязательного пребывания в очереди (2.6.15):

W= 0.00423.83⁴/4=0.886.

Найдем вероятность того, что суммарное время обслуживания и ожидания превзойдет величину t=0.5 (30 мин.). Применим (2.6.16):

Р(>0.5) =e^–5.217/2(1+0.886/4)(1–e^{–5.2174/2(1–3.83/4–1/4)})/(1–3.83/4–1/4))=0.7.

Таким образом, 88.6% клиентов обязательно проходят через очередь, причем 70% находятся в ней более получаса (правда, включая время обслуживания).

Вариант 2. Добавим к варианту 1 ограничение на количество мест для ожидания. Пусть k=16, тогда из (2.6.19) находим сначала

Р₀=1/(1+3.83+3.83²/2!+3.83³/3+3.83⁴(1–(3.83/4)¹⁷)/4!/(1–3.83/4))=0.00759

и, следовательно, из (2.6.21) получаем

=0.007593.83⁵(1–(3.83/4)¹⁶–16(3.83/4)¹⁶(1–3.83/4))/3/(4–3.83)²=5.82.

Поскольку Р₂₀=3.83²⁰0.00759/4!/4¹⁶=0.03397, используя (2.6.23), имеем для среднего времени ожидания обслуживания:

=5.82/20/(1–0.03397) =0.301 часа.(18 мин.)

Сравнивая варианты 1 и 2, видим, что при ограничении мест для ожидания, продолжительность ожидания сокращается более чем в три раза, причем это достигается ценой потери около 3.4% потенциальных клиентов (Р₂₀=0.03397).