pvt

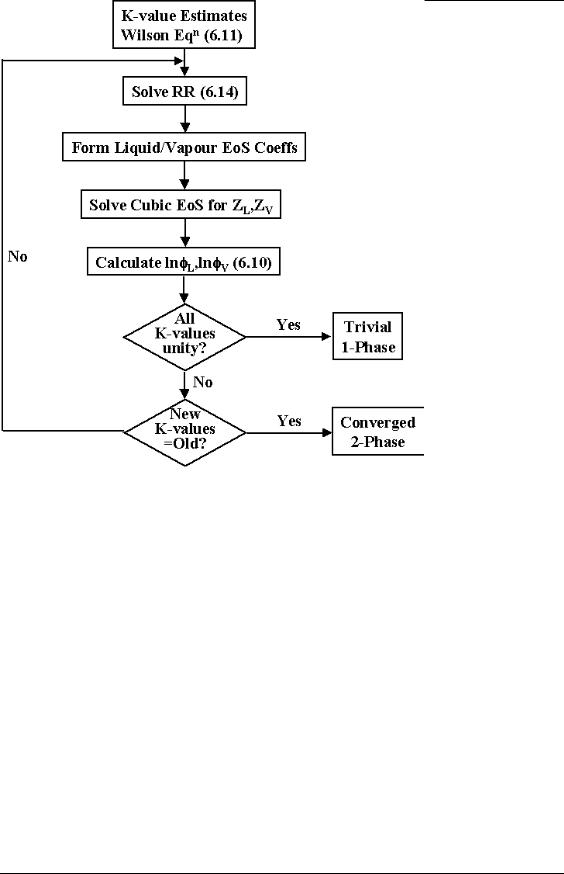
PVT Analysis

Given an estimate for the K-values, we must next determine the liquid/vapour split: this is the subject of the Rachford-Rice equation, which we will discuss in the next section. Assuming these compositions are available, we can then compute the component (Ai,Bi)’s and phase (A,B)’s which in turn enable us to calculate the liquid and vapour fugacity coefficients. These are then substituted back into (6.10) to give updated estimates for the K-values. This process continues until there is no change in the K-values between iterations – convergence, or all the K-values approach unity simultaneously – the trivial solution. The convergence to the trivial solution indicates the fluid of interest does not form a two-phase mixture at the pressure and temperature of interest.

Figure 38: Flow Diagram for the Successive Substitution Flash

The rate at which the scheme proceeds to convergence or triviality depends on the proximity to the critical point. For near-critical systems, convergence can take 100’s or even 1000’s of iterations. Various acceleration schemes have been proposed including the General Dominant Eigenvalue Method (GDEM): for details of GDEM, see Søreide. The fastest technique is to use a Newton scheme. The derivatives of the fugacity coefficients are readily derived. The major problem with a Newton scheme is

Roxar Oxford

71

12/12/12

PVT Analysis

convergence is only guaranteed if the initial estimate is close to the solution. Using a combination of good initial estimates, some advanced optimization techniques plus use of good physics to guide the solution when it encounters difficulties, fast Newton-based schemes are the norm in reservoir simulators like MORE and Eclipse 300.

6.1.1 Rachford-Rice Equation

Suppose we have one mole of feed [zi = ni/nT] which splits into V moles of vapour of composition y and L moles of liquid of composition x, then:

(6.12)	zi	Lxi Vyi	i 1, , N
and:
	N	N	N
(6.13)	xi yi		zi L V 1
	i 1	i 1	i 1

Combining these relationships with the definition of the K-value, (6.9) gives the Rachford-Rice equation:

		N	(Ki 1)
	(6.14)	F(V ) zi		0
			1 V (Ki 1)
		i 1

Under reasonable assumptions where at least one K-value is greater than 1 and one K- value is less than 1, the value of V which satisfies (6.14) must lie in the range:

(6.15)	Vmin V Vmax
where:
(6.16)	Vmin			1	0	Vmax			1	1
		1					1
				Kmax					Kmin

(Kmin,Kmax) are the minimum and maximum K-values, respectively. Between these lower and upper limits, F(V) is a monotonically decreasing function. Given an initial estimate for V, say:

(6.17)

V(0) 0.5(Vmin Vmax )

then a Newton scheme17 can be employed to find V. If the new value of V ever goes outside the range indicated by (6.15), a bisection-like technique can be employed to bring the solution into the physical space.

If the vapour fraction found from (6.14) is 0 < V < 1, then a physical 2-phase solution is possible. If V < 0 or V > 1, this indicates the solution is 1-phase, being either a liquid or vapour respectively.

17 In the simulation environment, we generally have the solution from the previous time step for the current grid cell.

Roxar Oxford

72

12/12/12

PVT Analysis

6.2 Stability Test

If the solution of the SS Flash indicates a Trivial solution and/or the Rachford-Rice solution generates a vapour fraction V < 0 or V > 1, then strictly we should do a further test to confirm this fluid is indeed single-phase at the local (p, T). This further check is called the Stability Test.

The GFE of the feed composition, z, is given by (6.1). Suppose we now attempt to split off an infinitesimal amount, , of a second phase of composition, y. Using a Taylor series expansion to first order, the GFE of feed minus the of the 2nd phase is:

		N
(6.18)	G(I ) G(0)	yi i (z)

i 1

The GFE of the trial phase is:

	N
(6.19)	G(II ) yi i ( y)

i 1

The trial phase is thermodynamically preferred if:

(6.20)	G G(I ) G(II ) G(0)	0
This can be simplified to show:
	N
(6.21)	G yi i y i z 0

i 1

By minimizing G, we can find out if (6.21) is satisfied and hence whether our fluid is unstable, i.e. 2-phase. It can be shown this is equivalent to requiring:

(6.22)	lnYi ln i ( y) ln zi ln i (z) 0

The Yi are interpreted as mole numbers: the composition y is given by:

		N
(6.23)	yi Yi	Yj
		j 1

The iterative solution of (6.22) proceeds very much like that of the SS Flash. The Wilson K-value correlation, (6.11), can be used to construct a liquid-like and vapour-like fluid from the feed:

(6.24)	Y LL	zi	Y VL z		K Wil
	i	KiWil	i	i	i

Each of these trial compositions are taken in turn. Firstly, a normalized composition is calculated from (6.23), then the fugacity coefficients of this composition and the feed are calculated and a new set of mole numbers calculated from (6.22). As with the Flash, we check for progress towards a trivial solution by seeing if all the K-values approach unity. If the system is unstable, the sum of the mole numbers at the solution will be greater than 1. If the first trial fails, the second is then tried. If they both fail we can conclude with

Roxar Oxford

73

12/12/12

PVT Analysis

reasonable confidence our fluid is single-phase. If the first trial succeeds, it is normal to still run the second trial. The composition calculated from the Stability test can be used to construct K-values to re-start the Flash. In the case where the 1st trial has succeeded, if the 2nd trial succeeds as well, the ratio of the two compositions will give a better set of K- values to re-start the Flash.

As with the Flash problem, around the critical point, convergence can be very slow. Onepoint GDEM18 can be used to accelerate the SS scheme or fullor quasi-Newton schemes are possible.

In the simulation environment, the Stability Test can be a computationally expensive way of generating very little information; i.e. the fluid is 1-phase. In its normal mode of operation, MORE tries to avoid the Stability Test calculation wherever possible. As was made clear when we looked at the Rachford-Rice problem, solutions outside the physical range are possible. Similarly, the equal fugacity conditions, (6.6) or (6.8) can still be solved although the solution cannot be guaranteed with the same rigour as when the vapour fraction lies within [0,1]. This procedure was termed Negative Flash by Whitson and Michelsen. Its principle value is in reservoir simulation where like the conventional flash it can re-use information from a previous time step, i.e. K-values, as a predictor for the solution at the current step. This is unlike the Stability Test, which starts from the two-sided Wilson estimates each time. A negative flash can be 10 times faster than a Stability Test calculation.

6.3 Saturation Pressure

The saturation pressure calculation is a special case of the Flash. For a bubble point we require V = 0, equivalent to the Rachford-Rice becoming:

	N
(6.25)	FB (V 0) zi (Ki 1) 0

i 1

For a dew point, V = 1, or:

(6.26)	FD (V 1) zi	(Ki 1) 0
	N
	i 1	Ki

By analogy with the Stability Test, mole numbers calculated from (6.22) must satisfy the condition:

	N
(6.27)	Yi 1

i 1

Søreide suggests a hybrid scheme for finding the (y, psat). The composition is updated using an iteration of (6.22) whilst the pressure is updated using an iteration of a Newton scheme on (6.27).

18 The Flash uses 2-point GDEM: see Søreide for details.

Roxar Oxford

74

12/12/12

PVT Analysis

As with the Stability Test, we should construct a liquid-like composition from our feed, (6.24), and look for a bubble point solution. If that fails, build the vapour-like composition and look for a dew point solution. If both searches fail, we are presumably at some temperature in excess of the Cricondentherm, see section 3.2.

6.4 Composition versus Depth

We have described how chemical potential is the force which drives the diffusion of components between liquid and phases until they have the same values in both phases, (6.6). In the presence of a gravitation field, this becomes modified to:

(6.28)

i (h) i (h0 ) M wi g(h h0 ) 0

i 1, , N

i(h0) is the chemical potential at the reference depth, h0, whilst i(h) is the value at the depth of interest, h: g is the acceleration due to gravity [9.81 m/s2]. Thus, given a composition z(h0), we can estimate the composition z at h from (6.28).

A number of assumptions are implicit in (6.28). The first and most contentious is the fluid column, which may stretch over several 100 ft, is in equilibrium. Fluid may be still entering the trap or it may be undergoing change in-situ. Movement of the rock strata can cause fluid movement, as can thermal gradients. The temperature gradient in a reservoir can vary between 0.5 oF/100ft and 4.0 oF/100 ft: a typical value is 2.0 oF/100 ft [3.65 oC/100 m]. These temperature gradients can induce connective flow in an attempt to equalize the temperature differences. Generally, temperature gradients seem to have the effect of reducing the size of the compositional variation predicted by (6.28) using the constant temperature assumption.

The other main driver to cause deviations from that predicted by (6.28) is the presence of asphaltic material in the reservoir fluid. Even in small quantities, they have the effect of exaggerating the compositional variation. Near-critical fluids also experience strong composition gradients though these may be predictable.

Putting these concerns to one side, (6.28) gives us a mechanism to estimate how composition may change with depth. Two possible systems are possible as indicated in the following two figures.

In the first diagram, the fluid column has a distinct Gas-Oil-Contact (GOC). The dew point pressure equals the bubble point pressure equals the reservoir pressure at the GOC. Above this, the vapour gets lighter at decreasing depth and the difference between the fluid [vapour phase] pressure and the dew point pressure increases. Below the GOC, the liquid gets heavier with increasing depth and the difference between the fluid [liquid phase] pressure and the bubble point pressure increases.

Roxar Oxford

75

12/12/12

PVT Analysis

Figure 39: Gas-Oil Contact

Figure 40: Critical Transition

In the second case, again the fluid gets heavier with depth so that the dew point pressure increases and the bubble point pressure decreases with increasing depth. Now however, the fluid makes a smooth transition from vapour to liquid without exhibiting a GOC: this is called a Critical Transition.

In the first case, sampling near the GOC, especially in the gas cap would be fraught with problems. Since the difference between the fluid and dew point pressure is quite low, it would not take much draw down for the fluid entering the well to be two-phase. It is clearly preferable to sample as high up and as low-down in the column as possible.

Roxar Oxford

76

12/12/12

PVT Analysis

7.Characterization

As we saw in section 2.8, most laboratory analyses of produced fluids end with some residual or plus fraction: typically, this will be C7+, C10+, C12+, etc. Even if we are able to obtain all the physical properties of the plus fraction needed to perform EoS calculations19, experience shows the fluid system usually requires a more detailed breakdown, especially for near-critical fluids.

The process of characterizing the plus fraction makes use of mathematical models of component distributions based on experimental observations. There are three main tasks:

1.Divide the plus fraction into a number of sub-fractions of known mole fractions.

2.Define the mole weight, specific gravity and boiling point of the sub-fractions: the socalled Inspection Properties.

3.Estimate the physical properties required by the EoS for the sub-fractions.

We will consider these three points in turn.

7.1 Molar Distribution Models

Accepting that the origin of the hydrocarbon accumulations we found nowadays is organic in nature20, then originally the molecules were large multi-ring aromatics and napthenes. Over the 10’s of millions of years the material has been buried, the material has been cooked more or less strongly depending on its depth of burial.

If all C-C bonds in all molecules are equally likely to be broken, then large molecules are more likely to broken up into smaller molecules. Thus, the idea that the distribution of molecules within plus fractions can be described by some exponentially decaying function would seem reasonable: this hypothesis is borne out by observation.

Of all the mathematical models for describing plus fraction molar distributions, the most powerful and widely used are those due to Whitson: see Søreide for details. The basis of Whitson’s model is the Gamma Distribution Model (GDM):

(7.1)	p(M )	(M	)( 1)			(M )
					exp
				( )

where:

19Mole weights, critical pressures, temperatures and volumes, acentric factors and BIPS.

20For an alternative explanation, see Prof. Thomas Gold’s hypothesis of The Hot Deep Biosphere, Copernicus, New York (1998).

Roxar Oxford

77

12/12/12

PVT Analysis

	(7.2)		(M N )

This 3-parameter model ( , , ) measures the probability p of finding a molecule of mole weight M within the plus fraction of mole weight MN+. The key parameter is which

defines the shape of the distribution: its value is usually 0.5 < < 2.5. A value of = 1 gives a pure exponential distribution and is the default value in the absence of any other information. If a compositional breakdown of the C7+ is available, say to C12+ or preferably C20+, this information can be used to set the value of by tuning the model to the measured data. The parameter can be interpreted as the minimum mole weight within the plus fraction: for a C7+ plus fraction, a value of = 90 is common. is the gamma function, details of which can found in most undergraduate texts on applied mathematics.

Figure 41: Whitson GDM for different values of

By definition, the integral of the GDM between [ , ] is unity:

(7.3) p(M )dM 1

Further, the plus fraction mole-weight satisfies the condition:

(7.4) Mp(M )dM M N

Integrating (7.1) between mole weight limits [Mi, M(i+1)] gives normalized mole fraction zi/zN+ of that interval. The recommended way of operation of the model was to split the plus fraction into the SCN groups up to some upper limit of C39, leaving a C40+ residual. These cuts should then be grouped back to give between three and five pseudocomponents. A typical split of a C7+ into five pseudo-components might then yield:

C7-10, C11-16, C16-20, C21-30, C31+.

Roxar Oxford

78

12/12/12

PVT Analysis

Whitson improved the GDM model by using the mathematical technique of Quadrature.

7.1.1 Quadrature

Certain definite integrals such as (7.3) can be approximated to a high degree of accuracy by a series summation:

	N
(7.5)	ab w(x) f (x)dx		i f (		i )
		w		x
	i 1

The choice of weighting function w(x) depends on the nature of the function f(x) and the

limits [a, b], these in turn fix the weights, wi , and nodes, xi , for this N-point approximation.

In the case of the GDM, we can define:

(7.6)	x		(M )						dx dM
so that (7.3) becomes:
							( 1)
			1		( x)				1
(7.7)	0							exp( x) dx 0		x( 1) exp( x)dx
									( )
		( )

Given the nature of this integral, involving as it does the term exp(-x) and the limits of zero and infinity suggests that the Laguerre-form of Quadrature is most appropriate where the function will be:

	(7.8)	f (x)	x( 1)
			( )

As was made clear in (7.5), the representation of the integral by the series summation is only an approximation although the quality of the approximation is improved by choosing a larger number of points, N. The nodes and weights for the 5-point GaussLaguerre Quadrature are shown in the table below: see Abramowitz and Stegun.

i		xi	wi
1	0.263	560 319 718	5.217 556 105 83E-01
2	1.413	403 059 107	3.986 668 110 83E-01
3	3.596	425 771 041	7.594 244 968 17E-02
4	7.085	810 005 859	3.611 758 679 92E-03
5	12.640	800 844 276	2.336 997 238 58E-05

Roxar Oxford

79

12/12/12

PVT Analysis

Having selected the number of points, N, the values for the weights and nodes can be looked up from a book of mathematical tables: see Abramowitz and Stegun.

7.1.2 Modified Whitson Method

Whitson’s modified method has an additional 4th parameter, , defined initially by:

	(0)			*
(7.9)		exp			1
			M N

and a modified -parameter, * defined by:

	(7.10)	*	(M N )
			xN

where xN is the value of the Nth node looked up from the tables and MN is the mole weight of the last pseudo-component. For a C7+ plus fraction, Whitson suggests MN = 2.5 M(C7+). The mole weights of the N pseudo-components are given by:

(7.11)

M i * xi

and the mole fractions from:

(7.12)

zi zN wi f (xi )

The function f(x) is given by:

(7.13)	f (x)	x( 1)		(1 ln )
		( )		x

As a quality check, we can back-calculate the plus fraction mole-weight from:

	N
(7.14)	M Ncal zi M i

i 1

If the value calculated from (7.14) disagrees with that measured, the value of should be adjusted and the mole weights and mole fractions re-calculated until (7.14) is satisfied.

Another feature of the modified Whitson method is its ability to simultaneously characterize several samples at once. Suppose we have M samples of fluid, each of which has a common plus fraction definition, say C7+. In practice, each of the samples will have a different plus fraction mole weight and distribution or shape parameter . Now by selecting an N, and MN, we can calculate a unique * from (7.10) and hence a unique set of mole weights from (7.11). Now using the [ , MN+] by sample, by calculate an [initial] by sample and hence a set of mole fractions, zi, by sample from (7.12). The mole weight check (7.14) is made for each sample and the appropriate ’s adjusted until the plus fraction mole-weights of all samples are honoured. Arguably, this technique has been the best advance in fluid modeling in the last 10 years.

Roxar Oxford

80

12/12/12