f / (x)≈ f / (x)≈

4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Численное дифференцирование применяется тогда, когда функцию невозможно продифференцировать аналитически, например, когда она задана таблично.

4.1. Простейшие формулы численного дифференцирования для первой производной

Из определения первой производной f / (x)= lim	f (x +	x)− f (x)
		x
x→0

пользовать для ее вычисления две простейшие приближенные формулы

f (x + h)− f (x), h

f (x)− f (x − h), h

естественно ис-

(4.1.1)

(4.1.2)

			соответствующие выбору фиксированных значений
			x = h	и x = −h . Здесь h > 0				- малый		пара-
		N +	метр - шаг. Формулы (4.1.1) и (4.1.2) называют правой
N0	α+		и левой разностными производными. Оценим их по-
	y = f (x)		грешности:			f (x + h)− f (x)
α-			r+	(x, h)=	f / (x)−					и
						h
N−			r− (x, h)=	f / (x)−	f (x)− f (x − h)		,	воспользовавшись
x − h x	x + h				h
			формулой Тейлора:

f (x ± h) = f (x)± f

/ (x)h +

f // (ζ± )

h2

, ζ+ (x, x + h), ζ- (x − h, x).

2

Подставив в r± (x, h) выражение (4.1.3), получим

f (x)+ f / (x)h +

f // (ζ+ )

h2

− f (x)

1

f // (ζ

)

+

r+ (x,h)= f / (x)−

2

=

f /

(x)h − f

/ (x)h −

h2

= −

h

2

h

Аналогично, r− (x, h)=

f // (ζ− )

h. Таким образом,

2

r

(x, h)

≤ 1 M

2

h,

M

2

= max

f // (x)

,

+

2

[x, x+h]

(x, h)

1 M

f // (x)

r

≤

2

h,

M

2

= max

.

−

2

[x−h, x]

(4.1.3)

f // (ζ+ )h . 2

(4.1.4)

Итак, формулы (4.1.1) и (4.1.2) имеют первый порядок точности по h . Геометрическая интерпретация этих формул показана на предыдущем рисунке. Естественно предположить, что лучшим по сравнению с (4.1.1) и (4.1.2) приближением f / (x)= tg α является тан-

генс угла наклона α0 секущей к графику y = f (x), проведенной через точки N−			и N+ . Со-
ответствующая формула приближения имеет вид
f / (x)≈	f (x + h)− f (x − h)	.	(4.1.5)
	2h
108

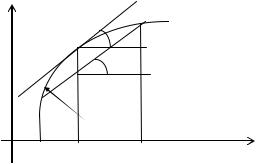
	N0	α N+
		α0
	N−	y = f (x)
	x − h x	x + h

лучим

f / (x), полученную по формуле (4.1.5), называют

центральной разностной производной. Оценим опять погрешность формулы (4.1.5). Для этого под-

ставим	в	выражение			для		погрешности
r (x, h)= f / (x)−		f (x + h)− f (x − h)					соответствую-
0		2h
щие разложения в ряд Тейлора:
f (x ± h)= f (x)± f / (x)h +			f // (x)	h2 ±			f (3)(ζ± )	h3 . По-
							6
		2

f (x)+ f / (x)h +

1

f //

(x)h2

+

1

f /// (ζ+ )h3

− f (x)

+ f / (x)h −

1

f // (x)h2

2

2

r (x, h)

= f / (x)−

6

+

0

2h

1

f /// (ζ

)h3

−

h2

h2

6

+

= f / (x)− f / (x)−

(f ///

(ζ+ )+ f /// (ζ− ))= −

(f /// (ζ+ )+ f /// (ζ− )).

2h

12

12

Следовательно, справедлива оценка погрешности

r (x, h)

≤

M 3

h2 , M

3

=

max

f (3)(x)

.

(4.1.6)

0

6

[x−h, x+h]

Таким образом, центральная разностная производная аппроксимирует производную f / (x) со вторым порядком точности относительно параметра h .

Для вычисления первой производной можно получить и еще более сложные и точные формулы. Однако в таких формулах с ростом порядка точности возрастает и число используемых значений функции. Например,

	f / (x)≈	f (x − 2h)− 8 f (x − h)+ 8 f (x + h)− f (x + 2h)		, где r(x, h)= O(h4 ).	(4.1.7)
		12h

4.2. Формулы численного дифференцирования для второй производной

Наиболее простой и широко применяемой для приближенных вычислений второй производной является следующая формула

	f // (x)≈	f (x − h)− 2 f (x)+ f (x + h)			.	(4.2.1)
			h2
	Она выводится из формулы f // (x)≈		f / (x)− f / (x −h)		, в которой первые производные
			h
	рассчитываются по формуле (4.2.1) по трем точкам x − h,				x и x + h . Формулу (4.2.1) часто

называют второй разностной производной. Покажем, что она имеет второй порядок точности

относительно

h .

Итак,

r(x, h)= f

// (x)−

f (x − h)− 2 f (x)+ f (x + h)

,

причем

f // (x)

f /// (x)

f (4)(ζ± )

h2

f (x ± h)= f (x)± f / (x)h +

h2 ±

h3 +

h4 .

Тогда

2

6

24

f

(x)− f / (x)h +

f // (x)

h2

−

f (3)(x)

h3

+

f (4)(ζ− )

h4

− 2 f (x)+ f (x)

r(x, h)

= f // (x)−

2

6

24

+

h2

109

f / (x)h +

f // (x)

h2 +

f (3)(x)

h3 +

f (4)(ζ+ )

h4

f // (x)h2 +

h4

(f (4)(ζ− )+ f (4)(ζ+ ))

2

6

24

+

24

= f // (x)−

=

h2

h4

(f (4)(ζ− )+ f (4)(ζ+ )).

h2

= −

M 4

24

Следовательно,

r(x, h)

≤

h2 , где M

4

=

max

f (4)(x)

.

(4.2.2)

12

[x−h, x+h

]

Для получения

f // (x) можно использовать формулы любого порядка точности. Например,

формула f // (x)≈

− f (x − 2h)+16 f (x − h)− 30 f (x)+16 f (x + h)− f (x + 2h)

(4.2.3)

12h2

имеет четвертый порядок точности относительно параметра h , но требует наличия значений функции в пяти точках.

4.3. Формулы численного дифференцирования, основанные на интерполяции алгебраическими многочленами

			Предположим, что в окрестности точки x функция y = f (x)								аппроксимируется неко-
торой другой функцией g(x), причем g(x)										в точке x легко вычисляется. Естественно в та-
кой ситуации попытаться воспользоваться приближенной формулой											f (k )(x)≈ g (k )(x).
			Пусть Pn (x) -				интерполяционный			многочлен степени n	с узлами интерполяции
x	0	< x	< ... < x	n	, x [x	0	, x	n	]. В этом случае	f (k )(x)≈ P(k )(x), 0 ≤ k ≤ n. Поскольку
		1								n
		Pn	(x) = f (x0 )+ f (x0 ; x1 )(x − x0 )+ f (x0 ; x1 ; x2 )(x − x0 )(x − x1 )+ ... + f (x0 ; x1 ;...; xn )(x − x0 )×

× (x − x1 )...(x − xn−1 ) = ∑n f (x0 ; x1 ;...; xk )ωk (x),

k =0

то для аппроксимации производных в общем случае при наличии неравномерной сетки узлов можно воспользоваться связью производных и разделенных разностей:

f (n)(x)≈ n! f

(x

0

; x ;...; x

n

)= P(n )(x).

(4.3.1)

1

n

Формула (4.3.1) имеет по крайней мере первый порядок точности. В частности при

n =1 f / (x)≈ f

(x

0

; x )=

f (x1 )

− f (x0 )

-

первая

разностная

производная;

при n = 2

1

x1

− x0

// (x)≈ 2 f (x

)=

2

f (x2 )− f (x1 )

f (x1 )− f (x0 ) =

x0 = x − h, x1 = x,

f

; x

; x

−

x

= x + h, x

− x

= 2h, =

x

− x

0

1

2

2

x

2

− x

x

− x

0

2

2

0

0

1

1

x2 − x1 = h, x1 − x0 = h.

f (x − h)− 2 f (x)+ f (x + h)

=

- вторая разностная производная.

h2

Если шаг сетки узлов постоянен, то можно вместо разделенных разностей использо-

вать конечные:

n y0

f (n )(x)≈

.

(4.3.2)

hn

4.4. Обусловленность формул численного дифференцирования

Несмотря на внешнюю простоту формул численного дифференцирования, их приме-

нение требует особой осторожности. Так как табличные значения

f (x) функции y = f (x)

непременно содержат ошибки, и эти ошибки являются неустранимыми, они прибавляются к погрешностям аппроксимации. Для уменьшения этой погрешности обычно уменьшают шаг h , но именно при малых шагах формулы численного дифференцирования становятся плохо

110

обусловленными и результат их применения может быть полностью искажен неустранимой ошибкой. Важно понимать, что действительная причина этого явления лежит не в несовершенстве методов вычисления производных, а в некорректности самой операции дифференцирования приближенно заданных функций.

Рассмотрим r (x, h)= f / (x)−

f (x + h)− f (x)

.

Это полная погрешность,

она склады-

h

f (x + h)− f (x)

вается

из погрешности

аппроксимации

r+ (x, h)= f / (x)−

и

неустрани-

h

мой

погрешности

r (x, h)=

1

[(f (x + h)− f (x + h))− (f (x)− f (x))].

Пусть

H

h

(f (x))

(x)− f (x)

r (x, h)

= max

= max

f

.

Тогда

можно оценить следующим образом:

H

r

≤

2

. Фактически это число будет числом обусловленности формулы (4.1.1), то есть

H

h

ϑ = 2

h .

(4.4.1)

Видно, что при h → 0 ϑ → ∞. Поэтому, несмотря на то, что погрешность аппрокси-

мации стремится к нулю при h → 0, полная погрешность r(x, h)= r

(x, h)+ r

=

1 M

2

h

+

2

+

H

2

h

будет неограниченно возрастать. Найдем hопт , при

1

2

котором

r(x, h)→ min. Для этого

необходимо,

r

r = 2 M 2h

+ h

чтобы r

/ (x, h)=

1

M

2

−

2

= 0. Отсюда

h

2

h2

hопт

= 2

M

.

(4.4.2)

2

hопт

h

Тогда rmin

= r(hопт )= 2

M 2 .

(4.4.3)

Таким образом, при использовании формул чис-

ленного дифференцирования необходимо обращать внимание на выбор шага h. Даже при

оптимальном выборе шага полная погрешность является величиной, пропорциональной	.
При k >1 формулы для вычисления f (k )(x) обладают еще большей чувствительностью к

ошибкам задания функций. Поэтому значения производных высокого порядка, найденные с помощью таких формул, могут быть очень неточными.

	Пример. Пусть						f (x)= ex задана на [0,1] с шагом h = 0.2 следующей таблицей:
	x			0.0					0.2				0.4				0.6				0.8				1.0
	f (x)			1.00000					1.22140				1.49182				1.82212				2.22554				2.71828
	Найдем f / (x) в узлах таблицы и оценим точность полученных данных. В точках
x = 0.0 и x =1.0				возможно применение только формул для левой и правой разностной про-
изводной:											f (0.2)− f (0.0)						1.22140 −1.00000
			f	/ (x	0	)= f / (0.0)=									=								=1.10700,
												0.2						0.2
			f	/ (xn )=			f / (1.0)=				f (1.0)− f (0.8)				=		2.71828		− 2.22554				= 2.46370.
												0.2					0.2

В остальных точках применим формулу (4.1.5), имеющую более высокий порядок точности:

111