Расчетно-графические задания

Задание 1

1. По заданным разностным уравнениям цифровых цепей проверьте их физическую реализуемость (каузальность), стационарность, линейность и устойчивость:

Таблица 1

Вариант	Разностное уравнение
1
2
3
4
5
6
7
8
9
0

Таблица 2

Подвариант	a	b	c	k
1	1	4	3	2
2	3	2	4	1
3	2	3	1	4
4	4	1	2	3
5	2	1	3	4
6	3	2	4	3
7	2	1	4	2
8	3	1	4	2
9	5	2	1	6
0	3	4	6	5

2. По разностному уравнению

• составьте структурную схему цепи

• определите импульсную характеристику устойчивой дискретной цепи (аналитически)

• постройте график импульсной характеристики

• рассчитайте АЧХ и ФЧХ цепи, постройте графики.

• постройте нуль-полюсную диаграмму, обозначьте область сходимости -преобразования ИХ.

Таблица 3

Вариант				Подва-риант
1	3.1	0	7	1	1	9	2
2	5.3	5	3	2	4	8	4
3	7.7	1	4	3	3	7	6
4	8.4	2	2	4	7	6	8
5	5.6	6	5	5	5	5	0
6	3	4	2.5	6	2	4	9
7	6	9	6.4	7	0	3	1
8	9	8	2.2	8	6	2	3
9	7	5	7.4	9	8	1	5
0	4	7	9.3	0	9	0	7

Задание 2

Сформируйте набор из последовательностей, элементы которых состоят из строк матрицы Адамара 5-го порядка. Матрица Адамара первого порядка равна

.

Матрицы Адамара более высокого порядка строятся в соответствии с рекурсивным выражением

.

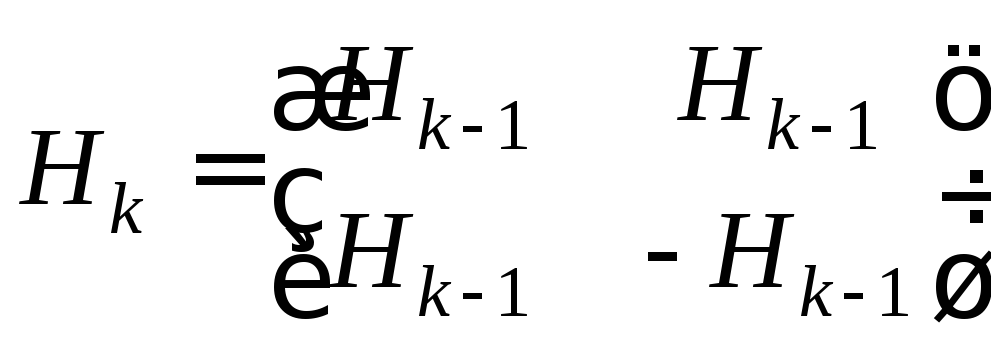Для сформированного набора последовательностей:

• покажите, что входящие в набор последовательности образуют базис;

• отобразите на разных графиках несколько базисных последовательностей;

• проверьте, является ли данный базис ортогональным;

• постройте базис, сопряженный сформированному базису;

• отобразите на разных графиках несколько последовательностей из сопряженного базиса;

• используя сформированный базис, разложите последовательность

,

параметры которой определены в таблице 4;

• отобразите на графике исходную последовательность;

• отобразите на графике последовательность, состоящую из коэффициентов разложения;

• постройте сокращенный набор коэффициентов разложения путем обнуления элементов, величина которых по модулю составляет не более 25-ти процентов от величины модуля максимального коэффициента разложения;

• отобразите сокращенный набор коэффициентов на графике;

• восстановите последовательность, используя сокращенный набор коэффициентов разложения;

• отобразите восстановленную последовательность на графике;

• рассчитайте энергию ошибки восстановления, а также отношение энергии ошибки восстановления к энергии исходной последовательности (в процентах).

Таблица 4

Вариант
1	0.65	0.95
2	0.92	0.76
3	0.7	0.93
4	0.97	0.68
5	0.76	0.93
6	0.92	0.77
7	0.88	0.94
8	0.75	0.97
9	0.91	0.73
10	0.72	0.96
11	0.56	0.99
12	0.99	0.57
13	0.68	0.89
14	0.71	0.88
15	0.93	0.76
16	0.89	0.9
17	0.69	0.93
18	0.95	0.78
19	0.78	0.97
20	0.94	0.83

Задание 3

Линейная инвариантная к сдвигу цепь задана разностным уравнением

,

параметры уравнения приведены в таблице 5. Для заданной цепи:

• постройте эквивалентную минимально-фазовую цепь, обладающую такой же амплитудно-частотной характеристикой;

• постройте нуль-полюсную диаграмму передаточной функции исходной цепи, обозначьте область сходимости;

• постройте нуль-полюсную диаграмму передаточной функции эквивалентной минимально-фазовой цепи, обозначьте область сходимости;

• рассчитайте АЧХ и ФЧХ исходной цепи, постройте графики;

• рассчитайте АЧХ и ФЧХ эквивалентной минимально-фазовой цепи, постройте графики;

• определите импульсную характеристику исходной цепи и отобразите ее на графике;

• определите импульсную характеристику эквивалентной минимально-фазовой цепи и отобразите ее на графике;

Таблица 5

Вариант
1	-0.61	0.32	-0.67	1.3
2	0.17	-0.37	1.2	-1.1
3	-0.29	-0.99	2.4	-1.7
4	0.65	0.1	-0.34	0.29
5	0.42	-0.13	0.22	-0.34
6	-0.39	-0.64	1.8	-1.3
7	0.82	-0.55	2	-3.6
8	-0.7	-0.1	0.15	-0.22
9	0.94	0.25	-0.6	1.1
10	-0.76	0.17	-0.16	0.29
11	0.21	0.24	-0.48	0.76
12	-0.67	0.82	-2.6	3.2
13	-0.89	-0.37	1.1	-1.4
14	0.57	-0.07	0.15	-0.13
15	0.75	0.65	-0.4	1.5
16	0.91	-0.75	2.6	-2.5
17	0.65	-0.76	0.45	-3.0
18	-0.67	-0.67	1.4	-1.7
19	0.42	0.22	-0.7	1.4
20	-0.39	0.35	-1.2	1.2

Задание 4

Некаузальная линейная инвариантная к сдвигу цепь задана разностным уравнением

,

параметры уравнения определены в таблице 6.

• преобразуйте заданную цепь в параллельное соединение рекурсивно вычислимых цепей;

• составьте структурную схему рекурсивно вычислимой реализации цепи;

• определите передаточную функцию цепи, постройте нуль-полюсную диаграмму, обозначьте область сходимости;

• рассчитайте АЧХ и ФЧХ цепи, постройте графики;

• определите (через обратное -преобразование передаточной функции цепи) импульсную характеристику цепи, отобразите ее на графике;

• рассчитайте численно импульсную характеристику цепи (65 отсчетов) путем подачи единичного импульса на вход разностных уравнений рекурсивно вычислимой реализации, отобразите полученные значения на графике.

Таблица 6

Вариант
1	0.56	0.53	-0.51	0.1	0.82
2	4.3	0.36	0.92	0.25	0.86
3	1.3	0.49	0.02	0.31	0.84
4	2.4	0.43	-0.07	0.41	0.74
5	2.1	0.44	0.2	0.14	0.43
6	2.0	0.45	0.37	0.1	0.55
7	3.0	0.43	0.12	0.06	0.12
8	0.37	0.54	-0.82	0.36	0.55
9	1.4	0.5	-0.75	0.21	0.7
10	0.31	0.73	-0.66	0.28	0.7
11	5.0	0.35	0.07	0.02	0.1
12	1.5	0.49	0.28	0.03	0.63
13	0.5	0.58	-0.28	0.41	0.57
14	1.9	0.45	0.17	0.03	0.59
15	4.1	0.38	-0.59	0.22	0.57
16	0.39	0.51	-0.39	0.14	0.31
17	4.2	0.37	0.01	0.16	0.74
18	1.1	0.6	0.12	0.07	0.79
19	4.0	0.39	-0.3	0.1	0.23
20	2.5	0.44	0.49	0.12	0.51

Задание 5

1. Рассчитать полосовой цифровой фильтр (ПФ) 3 порядка (для чётных подвариантов – фильтр Чебышёва, для нечётных – фильтр Баттерворта), предназначенный для фильтрации аналогового сигнала после его преобразования в цифровую форму.

Исходные данные:

• частота 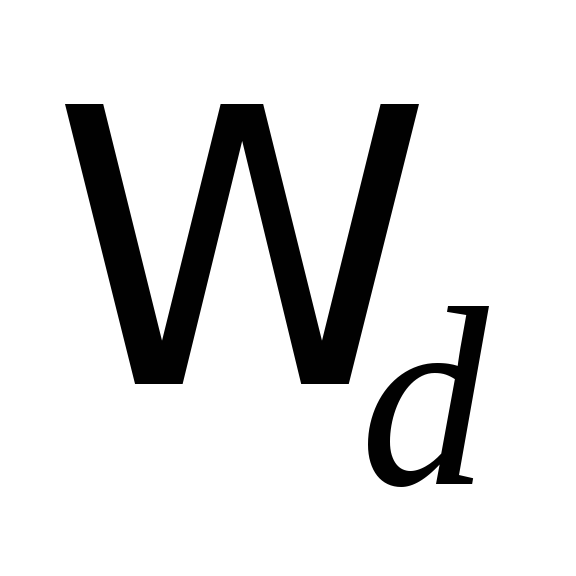дискретизации аналогового сигнала; нижняяи верхняяграницы полосы частот, занимаемой аналоговым сигналом – таблица 7;

• преобразование ФНЧ в полосовой фильтр провести для аналогового фильтра-прототипа;

• аналого-цифровую трансформацию ПФ провести методом билинейного преобразования;

• параметр для фильтра Чебышёва принять равным 0.4.

2. Построить структурную схему ЦФ в произвольной форме, при этом коэффициенты фильтра не должны быть комплексными. Записать разностное уравнение ЦФ. Рассчитать и построить графики АЧХ, ФЧХ и импульсной характеристики цифрового фильтра.

Таблица 7

Вариант	Частота	Частота	Частота дискретизации
1	3000	6000	30000
2	3500	7000	24000
3	5000	9000	35000
4	14000	26000	70000
5	6000	10000	38000
6	3000	6000	18000
7	3000	6000	37000
8	3000	6000	23000
9	13000	26000	80000
10	20000	48000	200000
11	7500	16000	50000
12	6300	11500	35000
13	3200	7100	18000
14	4600	8100	22000
15	4000	7500	32000
16	4000	8500	35000
17	3700	7200	25000
18	5200	9500	37000
19	13000	22000	65000
20	5800	10300	42000

Задание 6

Синтезируйте цифровой согласованный фильтр для сигнала, заданного в таблице 8. Сигнал наблюдается на фоне белого гауссовского шума с нулевым математическим ожиданием и дисперсией . Для синтезированного фильтра:

• рассчитайте и постройте график исходного сигнала;

• определите импульсную характеристику фильтра, постройте ее график;

• определите передаточную функцию фильтра;

• рассчитайте и постройте АЧХ и ФЧХ фильтра;

• рассчитайте и постройте графики модуля и аргумента спектральной плотности исходного сигнала;

• найдите автокорреляционную функцию исходного сигнала, рассчитайте и постройте ее график;

• определите аналитическое выражение отклика согласованного фильтра, получаемого при воздействии на его вход исходного сигнала, отобразите его на графике;

• рассчитайте методом быстрой свертки отклик согласованного фильтра, получаемый при подаче на его вход заданного сигнала; используйте для этого стандартные функции вычисления БПФ реализованные в пакетах универсального программирования типа MathCAD, MatLab и т.п.; сравните полученный результат с результатами расчетов, полученных в предыдущем пункте;

• найдите отношение сигнал/шум на входе и выходе согласованного фильтра.

Таблица 8

Вариант	Сигнал
1		4.0
2		2.4
3		1.5
4		0.8
5		2.2
6		5.2
7		7.4
8		3.6
9		8.1
10		2.7
11		3.2
12		6.4
13		7.9
14		8.3
15		4.1
16		2.8
17		3.4
18		5.3
19		2.8
20		1.9

Задание 7

Сигнал, передаваемый по каналу связи, подвергается воздействию помехи в соответствии с моделью

,

где – наблюдаемая последовательность,– полезный сигнал,– стационарный белый шум с нулевым средним и дисперсией. Статистические свойства полезного сигнала описываются уравнением авторегрессии-скользящего среднего (АРСС)

,

где – последовательность независимых случайных величин с нулевым средним и дисперсией. Для подавления шума используется цифровой трансверсальный фильтр порядка, определяемый выражением

,

где – оценка полезного сигнала,,– коэффициенты трансверсального фильтра.

Значения параметров полезного сигнала и шума приведены в таблице 9.

• рассчитайте и постройте автокорреляционную функцию и спектральную плотность мощности последовательности ;

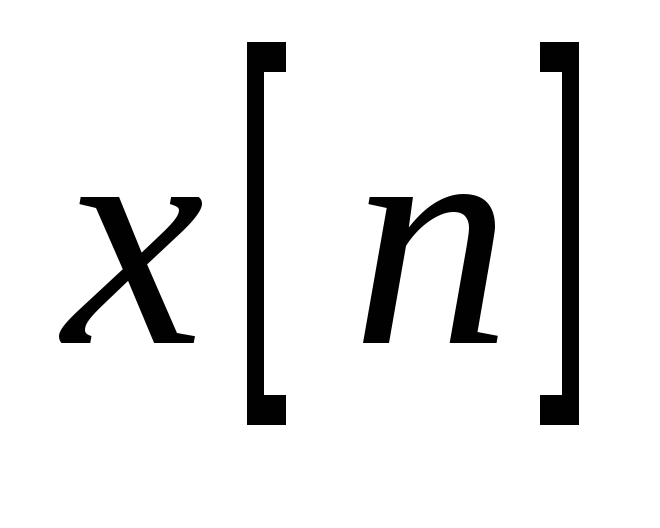• рассчитайте коэффициенты трансверсального фильтра, исходя из условия обеспечения минимума дисперсии ошибки оценивания

,

где – ошибка оценивания,– оператор усреднения по ансамблю реализаций;

• рассчитайте и постройте импульсную характеристику, АЧХ и ФЧХ синтезированного фильтра;

• рассчитайте дисперсию ошибки оценивания.

Таблица 9

Вариант
1	0.82	0.46	0.59	-1.4	2.1	1.9	8
2	0.17	0.86	-0.74	2.9	-1.3	-1.7	3
3	0.71	0.78	0.57	2.2	1.7	-0.55	15
4	0.3	0.99	0.15	-0.59	-1.9	1.8	17
5	0.09	0.61	-0.43	-2.5	1.5	0.73	18
6	0.15	0.27	-0.52	1.5	2.0	-1.1	6
7	0.99	0.84	0.75	-0.3	-0.57	2.2	3
8	0.53	0.38	0.17	1.7	1.4	-2.4	16
9	0.6	0.68	-0.49	-1.6	0.29	2.0	13
10	0.45	0.28	0.7	-1.9	-2.8	0.95	5
11	0.06	0.59	0.15	2.6	0.68	0.33	19
12	0.78	0.84	-0.43	-0.33	-1.2	2.6	14
13	0.52	0.49	0.97	0.94	1.9	-0.47	10
14	0.88	0.74	0.82	0.86	1.3	0.24	12
15	0.96	0.46	-0.19	-1.8	-1.8	-1.9	7
16	0.54	0.74	0.82	2.2	2.6	1.6	11
17	0.86	0.48	0.67	-1.5	2.2	1.8	8
18	0.67	0.39	0.59	2.7	-1.4	-1.8	10
19	0.75	0.68	-0.37	-0.61	-1.8	1.7	16
20	0.91	0.73	0.74	1.8	1.5	-2.5	14

Задание 8

На вход линейной инвариантной к сдвигу цепи поступает белый шум с нулевым средним значением и дисперсией . Импульсная характеристика цепи определена в таблице 10. Для заданных параметров цепи и шума:

• отобразите на графике импульсную характеристику цепи;

• определите передаточную функцию цепи;

• постройте АЧХ и ФЧХ цепи;

• определите спектральную плотность мощности и корреляционную функцию последовательности на выходе цепи, отобразите их на графике.

Таблица 10

Вариант	Имп. хар-ка	Вариант	Имп. хар-ка
1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

СПРАВОЧНЫЙ МАТЕРИАЛ

1. Алгебраические модели. Группы, поля, пространства

Множество элементов,,,называется группой, если определена бинарная операция, которая каждой паре элементов,ставит в соответствие элементтак, что выполняются свойства (аксиомы группы):

а) (замкнутостьпо отношению к операции);

б) (ассоциативность операции);

в) (существование нейтрального элемента);

г) (существование обратного элемента для каждого элемента группы).

Группа называется коммутативной (абелевой) если.

Множество элементов,,,называется полем, если на нем определены две бинарные операциии, условно называемые сложением и умножением, такие, что выполняются аксиомы поля:

а) является коммутативной группой по сложению;

б) совокупность всех ненулевых элементов является коммутативной группой по умножению;

в) , (дистрибутивность сложения и умножения).

Множество элементов,,,называется линейным (векторным) пространством над полем, а элементы множестваназываются векторами, если наопределены две бинарные операции – сложение векторов (+) и умножение вектора на скаляр (), такие, что

I) есть коммутативная группа по сложению векторов.

II) Операция умножения вектора (,,…) на скаляр (,,…) удовлетворяет следующим условиям:

а) (замкнутость пространства относительно умножения вектора на скаляр);

б) (ассоциативность умножения вектора на скаляр);

в) ,(дистрибутивность сложения векторов и умножения вектора на скаляр);

г), где– элемент поля(скаляр), нейтральный относительно операции умножения скаляров в поле.

Метрикой (расстоянием) на произвольном множественазывается вещественная функция (или функционал¹), определенная для любой пары элементови удовлетворяющая следующим условиям:

а) , итолько если;

б) (симметрия);

в) (неравенство треугольника).

Множество , на котором задана метрика, называется метрическим пространством.

Пусть – линейное пространство над полем. Функция (функционал)называетсянормой вектора, если она удовлетворяет следующим условиям:

а) , причем, только если;

б) (неравенство треугольника);

в) .

Пусть – линейное пространство над полем(или). Функция (функционал)называетсяскалярным произведением, если она удовлетворяет следующим условиям:

а) ;

б) ;

в) , причем, только если.

В пространстве со скалярным произведением выполняется неравенство Шварца

или,

на основе которого может быть введено понятие угла между векторами(только для пространства над полем), такого что

.

Совокупность векторов линейного пространства является линейно независимой, когдав том и только в том случае, еслипри всех(здесь– количество векторов).

Если в пространстве можно найтилинейно независимых элементов, а любыеэлементов этого пространства линейно зависимы, то пространствоимеет размерность. Если вможно указать систему изпроизвольного конечного числа линейно независимых векторов, то говорят, что пространствобесконечномерно.

Базисом -мерного пространстваназывается любая система излинейно независимых векторов. Базисом бесконечномерного пространства является бесконечная совокупность векторов, такая, что любое ее конечное подмножество линейно независимо.

2. Прямое и обратное -преобразование

Прямое -преобразование последовательностиопределяется выражением

.

Обратное -преобразование

,

где – контур, расположенный в области сходимости и охватывающий начало координат, направление обхода контура – против часовой стрелки.

Теорема о вычетах:

,

где – изолированные полюсы, находящиеся внутри контура интегрирования. Если– полюс порядка, то

.

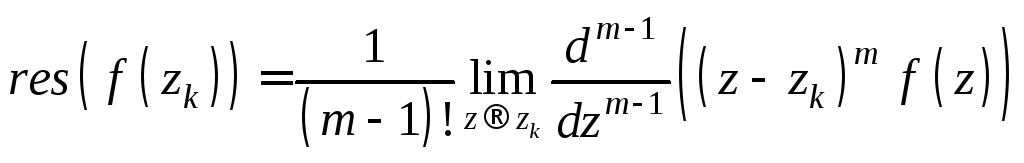Свойства -преобразования:

а) линейность

б) сдвиг последовательности

в) отражение последовательности

г) умножение на экспоненту

д) умножение на линейную последовательность

е) переход к комплексно-сопряженной последовательности

ж) свертка последовательностей

з) произведение последовательностей

3. Прямое и обратное преобразование Фурье

Прямое преобразование Фурье определяется выражением

.

Для абсолютно суммируемой последовательности ряд в правой части выражения сходится равномерно к непрерывной функции аргумента.

Обратное преобразование Фурье определяется выражением

, .

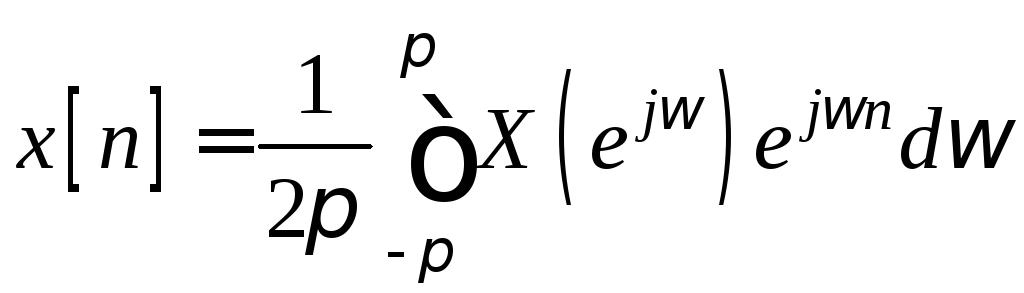4. Формулы Эйлера

,

,

.

5. Некоторые неравенства

,

,

–неравенство Коши – Буняковского (Шварца)

6. Свойства -функции Дирака

а) , б).

7. Формула суммирования Пуассона

.

8. Спектральные плотности некоторых сигналов

а) ,

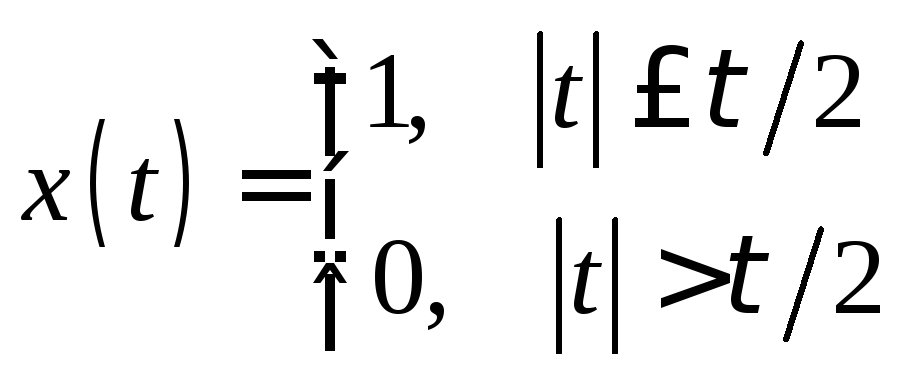
б) ,

в) .

9. Некоторые числовые суммы

а) , б),

в) .

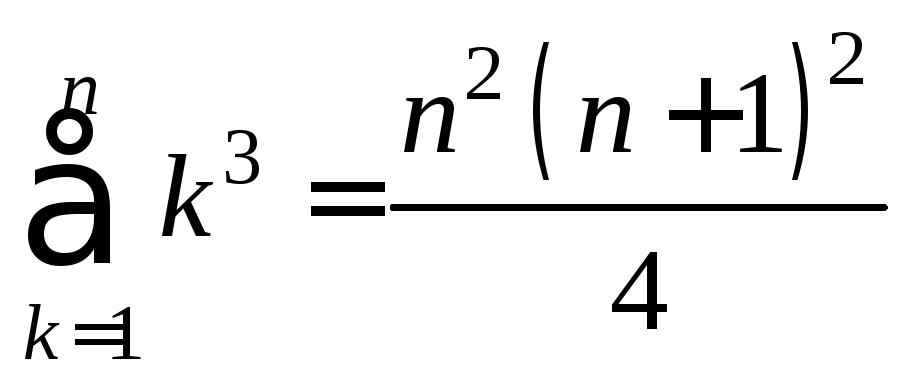10. Геометрическая прогрессия

Сумма геометрической прогрессии

, при ,

где ,,– первый член,– знаменатель прогрессии.

Частичная сумма геометрической прогрессии .
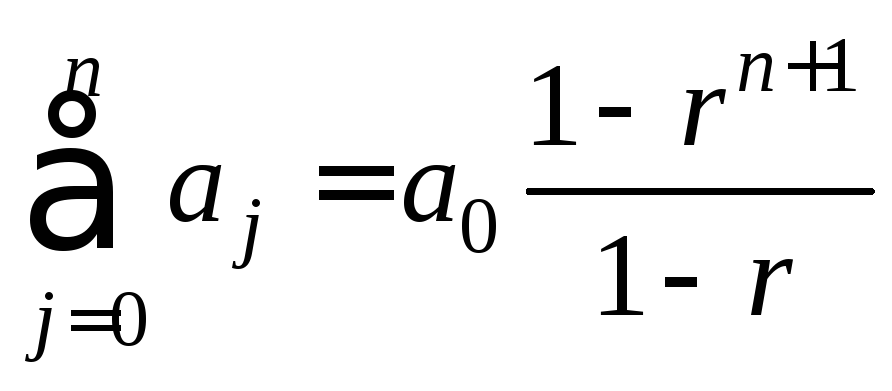