
ЧИСЛЕННЫЕ МЕТОДЫ
Метод конечных разностей (МКР)
Эффективное решение крупных естественно-научных и промышленных задач сегодня не возможна без применения ЭВМ. Технология исследования сложных проблем, основанная на построении и анализе с помощью ЭВМ математических моделей изучаемого объекта, называется вычислительным экспериментом.
Схема исследования какого-либо физического объекта, явления, процесса (вычислительный эксперимент) следующая:

Формулируются основные законы, управляющие данным объектом исследования (отбрасываются факторы, являющиеся не существенными для хода процесса);
Строится соответствующая математическая модель, обычно представляющая собой запись законов сохранения в форме системы уравнений (алгебраических, дифференциальных, интегральных);
Ищется решение математической задачи. На этом этапе возникает необходимость применения численных методов и использования ЭВМ. Под численным методом понимается такая интерпретация мат. модели (дискретный аналог, дискретная модель), которая доступна для ЭВМ (есть простые действия взамен интегралов, дифференциалов и т.д.). Как правило сегодня это алгебраический аналог системы уравнений мат.физики;
Для реализации численного метода составляется программа для ЭВМ; отладка – проверка соответствия результатов математической модели тестовым задачам;
Полученные результаты изучаются с точки зрения их соответствия исследуемому явлению и при необходимости вносятся исправления в численный метод и корректируется математическую модель.
Предметом данного курса является этап построения, исследования и программной реализации численного метода – МКР, хотя существует целый ряд равноценных численных методов (МКЭ, МГЭ,ММ и Я и др.)с точки зрения получения адекватного результата.
Схематично любой численный метод решения систем дифференциальных или интегральных уравнений можно разделить на следующие шаги:
Строится дискретный аналог области непрерывного изменения аргумента – конечное множество точек, называемое сеткой. Сетка один из основных признаков численного метода.
Водится в рассмотрение сеточная функция, определенная только в узлах сетки.
На сетке производится дискретизация математической модели, состоящая в приближенной замене производных и интегралов алгебраическими соотношениями сеточных функций, получаем алгебраический аналог математической модели. Способ дискретизации и составляет суть того или иного численного метода.
Тем или иным методом решается система алгебраических уравнений. Часто дискретизация производится с ориентацией на какой-либо эффективный метод решения алгебраической задачи.
Говорят, что ЧМ сходится, если при неограниченном росте числа алгебраических уравнений (узлов сетки) решение дискретной задачи стремится к решению исходной задачи. ЧМ устойчив, если в процессе счета погрешности округления не накапливаются, не искажают значительно конечный результат.
Основные понятия
МКР, или метод сеток, в настоящее время является одним из наиболее распространенных методов приближенного решения краевых задач.
Суть метода в следующем:
Область непрерывного изменения аргумента (отрезок, прямоугольник и т.д.) заменяется конечным (дискретным) множеством точек (узлов), называемым сеткой.
Вместо функции непрерывного изменения аргумента рассматриваются функции дискретного аргумента, определенные в узлах сетки и называемые сеточными функциями.
Производные, входящие в дифференциальные уравнения и краевые условия, заменяются (аппроксимируются) разностными соотношениями, т.е. линейными комбинациями значений сеточных функций в некоторых узлах сетки.
В результате краевая задача для дифференциального уравнения заменяется системой линейных, если исходная задача была линейной, алгебраических уравнений (системе разностных уравнений) – разностной схемой.
Если, полученная таким образом задача разрешима и ее решение при измельчении сетки приближается (сходится) к решению исходной задачи для дифференциального уравнения, то оно и принимается за приближенное решение исходной задачи.
Несмотря на внешнюю простоту метода, прежде, чем приступить к решению конкретной задачи, необходимо уметь дать ответы на следующие вопросы:
как выбрать сетку?
Как написать разностную схему?
Насколько хорошо разностная схема аппроксимирует исходную задачу?
Устойчива ли разностная схема и в каком смысле?
Какова скорость сходимости решения разностной задачи к решению исходной задачи?
СЕТКИ И СЕТОЧНЫЕ ФУНКЦИИ
Итак, заменим область непрерывного изменения аргументов G искомой функции Т некоторым конечным множеством точек, лежащих в этой области. Это множество назовем разностной сеткой, сами точки – узлами сетки, а функции, определенные на этой сетке, - сеточными функциями.
Свойства разностного решения и, в частности, его близость к точному решению зависит от выбора сетки. Расположение узлов сетки в области может быть произвольным и определяться спецификой решаемой задачи. Рассмотрим несколько примеров
равномерная сетка на отрезке
В простейшем случае
одномерной задачи можно ввести равномерную
сетку. Для этого [0,l]
- отрезок, область изменения аргумента
разобьем точками
![]()
![]() на
на![]() равных частей длины
равных частей длины![]() ,
рис 1.
,
рис 1.
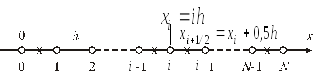
Рис.1. Разностная сетка на отрезке
Множество точек
![]()
![]() называется равномерной сеткой на отрезке
[0,l]
и обозначается
называется равномерной сеткой на отрезке
[0,l]
и обозначается
![]() ,h
– шаг сетки.
,h
– шаг сетки.
В качестве области
определения сеточных функций кроме
узлов, называемых еще целыми
точками,
часто используют полуцелые
точки
![]() ,
отмеченные на рис.1 крестиками.
,
отмеченные на рис.1 крестиками.
неравномерная сетка на отрезке
Рассмотрим тот же
отрезок [0,l].
Введя произвольные точки
![]() ,
разобьем его наN
частей. Тогда получим сетку
,
разобьем его наN
частей. Тогда получим сетку
![]() с шагом
с шагом![]() ,
который зависит от номераi
узла
,
который зависит от номераi
узла
![]() .
Если
.
Если![]() хотя бы для одного номераi
, то
хотя бы для одного номераi
, то
![]() - неравномерная сетка.
- неравномерная сетка.
Очевидно, что
![]() .
.
равномерная сетка на плоскости
Рассмотрим множество
функций
![]() двух аргументов. В качестве области
определения выберем прямоугольник
двух аргументов. В качестве области
определения выберем прямоугольник
![]() ,
,
например, ![]() Рис.2.
Рис.2.

Рис.2. Разностная сетка на плоскости
Построим на каждом
отрезке ![]() сетку
сетку
![]() с шагом
с шагом![]() .
Множество узлов
.
Множество узлов![]() с координатами
с координатами![]() (
(![]() )
назовем сеткой в прямоугольнике
)
назовем сеткой в прямоугольнике![]()
![]()
Эта сетка равномерна
по каждому из переменных
![]() и
и![]() .
Если хотя бы одна из сеток
.
Если хотя бы одна из сеток![]() неравномерна, то сетка
неравномерна, то сетка![]() называется неравномерной. Если
называется неравномерной. Если![]() ,
то сетка называется квадратной,
,
то сетка называется квадратной,![]() - прямоугольной.
- прямоугольной.
Приведем пример
неравномерной изометрической сетки на
плоскости. Область G
представляет собой кольцо, покроем его
окружностями
![]() ,
где
,
где![]() и лучами
и лучами![]() ,
рис.3.
,
рис.3.
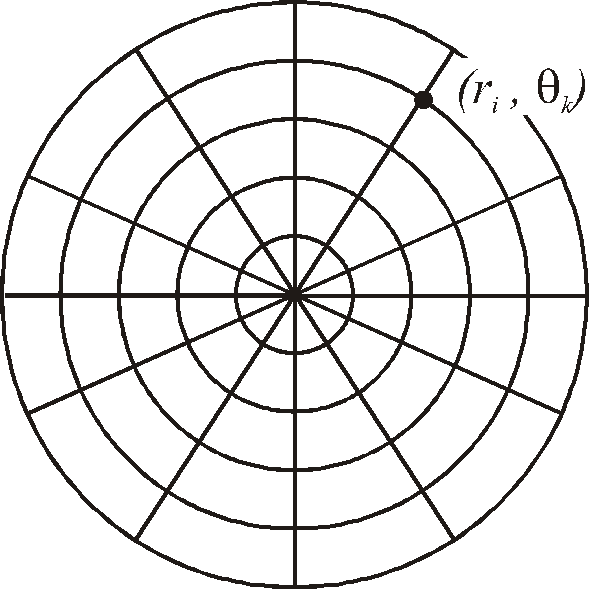
Рис.3. Разностная сетка на плоскости кольца
сетка на плоскости в произвольной области
Пусть на плоскости
![]() дана областьG
сложной формы с границей Г
рис.4..
Проведем прямые
дана областьG
сложной формы с границей Г
рис.4..
Проведем прямые
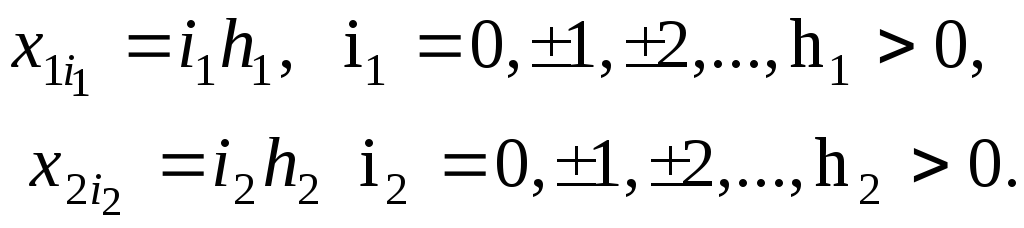

Рис.4. разностная сетка на области сложной формы
Тогда на плоскости
получим сетку с узлами
![]() ,
,![]() .Эта сетка равномерна
по каждому направлению. Нас интересуют
только те узлы, которые принадлежат
областиG
с границей
Г
.Эта сетка равномерна
по каждому направлению. Нас интересуют
только те узлы, которые принадлежат
областиG
с границей
Г
![]() .
.
Узлы, попавшие
внутрь G,
назовем внутренними узлами и обозначим
их совокупность
![]() .
Точки пересечения прямых
.
Точки пересечения прямых![]() с границейГ
назовем граничными узлами, а их множество
обозначим
с границейГ
назовем граничными узлами, а их множество
обозначим
![]() .
Видно, что имеются граничные узлы,
которые отстоят от ближайших к ним
внутренних узлов на расстояния меньшем
.
Видно, что имеются граничные узлы,
которые отстоят от ближайших к ним
внутренних узлов на расстояния меньшем![]() .
Таким образом, сетка
.
Таким образом, сетка![]() для областиG
неравномерна вблизи границы.
для областиG
неравномерна вблизи границы.
Рассматривают два возможных способа задания граничных условий для сложной области:
- ввести дополнительные узлы в точках пересечения линий сетки с границей и в них задать граничные условия;
- границу области аппроксимировать ломаной, проходящей через ближайшие к границе естественные узлы и перенести по определенному закону граничные условия на эту ломаную линию .
Для решения,
например, одномерных нестационарных
задач, используют произведение сеток
– сетки по координате и сетки по времени,
называемой пространственно-временной
сеткой
![]() .
Совокупность
узлов, лежащих на линии
.
Совокупность
узлов, лежащих на линии
![]() ,
называютi
– м слоем.
,
называютi
– м слоем.
Вопрос оптимального выбора шага сетки и тем самым количества ее узлов является непростым. С одной стороны, чем большая требуется точность, с которой необходимо получить решение, тем более мелкий шаг желателен. С другой стороны, слишком мелкий шаг значительно увеличивает число неизвестных. Очевидно, должны существовать некоторые оптимальные сетки со сравнительно небольшим числом узлов, называемыми реальными сетками или грубыми.
Построение разностной схемы проводится таким образом, чтобы получаемая в результате решения сеточная функция была как можно ближе к искомой непрерывной функции.
Вместо функций
![]() непрерывного аргумента
непрерывного аргумента![]() будем рассматривать сеточные функции
будем рассматривать сеточные функции![]() , т.е. функции точки
, т.е. функции точки![]() ,
являющейся узлом сетки
,
являющейся узлом сетки![]() в виде вектора
в виде вектора![]() .
.
Для оценки близости приближенного решения (решения на сетке) к точному решению исходной краевой задачи можно использовать два способа
Производится интерполяция сеточной функции на все точки области G, после чего определяется норма разности
 .
.Точное решение
 преобразуется в сеточную функцию
преобразуется в сеточную функцию (
( - одно из возможных обозначений сеточных
функций), после чего, определив сеточную
норму
- одно из возможных обозначений сеточных
функций), после чего, определив сеточную
норму ,
оценивается погрешность приближенного
решения в этой норме. На практике в
качестве сеточных норм используются:
,
оценивается погрешность приближенного
решения в этой норме. На практике в
качестве сеточных норм используются:
а) сеточный
аналог чебышевской нормы в пространстве
непрерывных функций С
![]()
б) сеточный
аналог гильбертовой нормы в
![]()
![]()
![]() ,
гдеh=h
в одномерном случае и
,
гдеh=h
в одномерном случае и
![]() в двумерном.
в двумерном.
Тогда если при
бесконечном дроблении сетки величина
![]() ,
то можно говорить о близости решения
разностной и краевой задачи.
,
то можно говорить о близости решения
разностной и краевой задачи.
АППРОКСИМАЦИЯ ППРОИЗВОДНЫХ. ПОРЯДОК АППРОКСИМАЦИИ.
ПОСТРОЕНИЕ РАЗНОСТНЫХ СХЕМ.
Решение исходной
задачи, таким образом, сводится к
нахождению числовых значений функции
![]() в точках сетки на соответствующей
области. Для приближенного вычисления
этой таблицы необходимо дифференциальный
оператор краевой задачиА,
заданный в классе непрерывных функций,
приближенно заменить (аппроксимировать)
разностным оператором
в точках сетки на соответствующей
области. Для приближенного вычисления
этой таблицы необходимо дифференциальный
оператор краевой задачиА,
заданный в классе непрерывных функций,
приближенно заменить (аппроксимировать)
разностным оператором
![]() ,
заданном на множестве сеточных функций.
Разностный аналог, аппроксимирующий
исходную краевую задачу, можно построить
различными способами. В связи с этим
возникает задача построения такой
разностной схемы, которая была бы
оптимальной в определенном смысле.
Обычно требуют, чтобы построенная
разностная схема на сравнительно грубых
сетках обеспечивала необходимый уровень
точности для получаемого приближенного
решения. Среди множества возможных
конструктивных подходов к построению
разностных аналогов для дифференциальных
операторов выделим основные:
,
заданном на множестве сеточных функций.
Разностный аналог, аппроксимирующий
исходную краевую задачу, можно построить
различными способами. В связи с этим
возникает задача построения такой
разностной схемы, которая была бы
оптимальной в определенном смысле.
Обычно требуют, чтобы построенная
разностная схема на сравнительно грубых
сетках обеспечивала необходимый уровень
точности для получаемого приближенного
решения. Среди множества возможных
конструктивных подходов к построению
разностных аналогов для дифференциальных
операторов выделим основные:
- метод формальной замены производных конечно-разностными выражениями;
- интегро-интерполяционный метод;
- вариационные методы построения разностных схем;
- метод неопределенных коэффициентов.
Метод формальной замены производных конечно-разностными выражениями. Метод конструирования разностных схем с помощью замены производных конечно-разностными выражениями основан на использовании разложения в ряд Тейлора достаточно гладких функций. Заменим производную, входящую в дифференциальной уравнение, разностным соотношением, содержащим значение сеточной функции в нескольких узлах сетки, образующих некоторую определенную конфигурацию. Такая совокупность узлов называется шаблоном. Узлы, в которых разностная схема записана на шаблоне, называют регулярными, а остальные узлы – нерегулярными. Рассмотрим возможные способы аппроксимации дифференциального оператора вида:
![]() (1)
(1)
определенного на
множестве непрерывных функций в области
G={d<x<b},
имеющих ограниченные производные
третьего порядка включительно. Пусть
![]() - равномерная сетка на отрезке. Тогда
наиболее естественный способ замены
производной основывается на определении
производной как предела
- равномерная сетка на отрезке. Тогда
наиболее естественный способ замены
производной основывается на определении
производной как предела
![]() .
.
Если зафиксировать h в этом равенстве, то получим приближенную формулу для первой производной через конечные разности
![]() .
.
Или в k-м узле имеем правое разностное отношение
![]() (2)
(2)
Аналогично вводится левое разностное соотношение
![]() .
(3)
.
(3)
Можно рассматривать и линейную комбинацию (2) и (3)
![]() ,
(4)
,
(4)
где
![]() - любое вещественное число. При
- любое вещественное число. При![]() получим центральное разностное
соотношение
получим центральное разностное
соотношение
![]() .
(5)
.
(5)
На рис.5 представлена геометрическая интерпретация производной в точке и ее разностная аппроксимация. Линия D отражает истинное значение производной в точке С, правую разность – линия СВ, левую – АС, центральную – АВ. Значение тангенса угла наклона прямой АВ ближе к значению тангенса прямой D.

Рис.5. Геометрическая интерпретация разностей
При замене оператора
![]() разностным выражением (2) –(4) допускается
погрешность
разностным выражением (2) –(4) допускается
погрешность![]() называемаяпогрешностью
аппроксимации оператора
А
разностным оператором
называемаяпогрешностью
аппроксимации оператора
А
разностным оператором
![]() в точкеx.
в точкеx.
Для вычисления
оценки
![]() разложимT(x)
в каждом внутреннем узле
разложимT(x)
в каждом внутреннем узле
![]() сетки
сетки![]() в ряд Тейлора:
в ряд Тейлора:
![]() .
(6)
.
(6)
Тогда в точке
![]() получим следующие выражения, соответствующие
разностным соотношениям (2)- (5):
получим следующие выражения, соответствующие
разностным соотношениям (2)- (5):
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Факт аппроксимации в точке называют часто локальной аппроксимацией. Тогда из равенств (6)-(10) следует, что порядок локальных аппроксимаций оператора в узловой точке сетки разностными операторами (2)- (5) равен единице в первых трех случаях и двум – в последнем.
Отметим, что
разностная производная (2) является
правой относительно узла
![]() и в то же время левой относительно узла
и в то же время левой относительно узла![]() .
Относительно полуцелой точки
.
Относительно полуцелой точки![]() эта же производная будет центральной.
Поэтому разностная производная (2)
аппроксимирует производнуюdT/dx
с первым порядком точности в узлах k
и k+1
и со вторым порядком в полуцелой точке
k+1/2.
эта же производная будет центральной.
Поэтому разностная производная (2)
аппроксимирует производнуюdT/dx
с первым порядком точности в узлах k
и k+1
и со вторым порядком в полуцелой точке
k+1/2.
Таким образом, видим, что выбор шаблона существенно влияет на свойства разностного оператора.
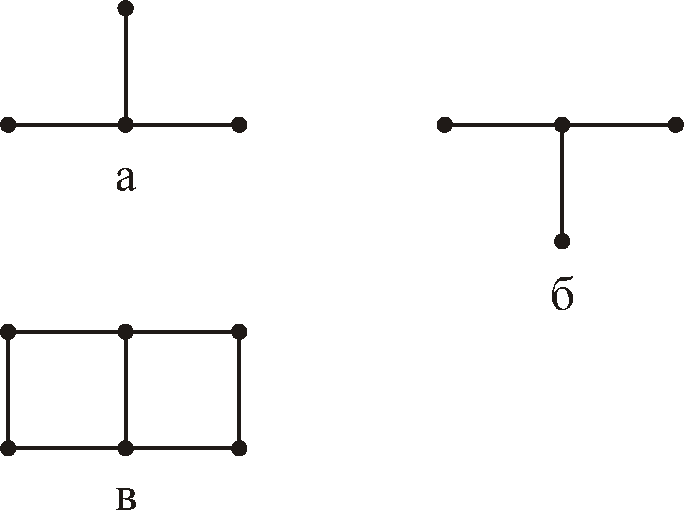
Рис.6. Виды шаблонов
Рассмотрим
аппроксимацию второй производной
![]() .
В отличие от первой производной, для
которой достаточно двухточечного
шаблона, для второй производной выберем
трехточечный шаблон (
.
В отличие от первой производной, для
которой достаточно двухточечного
шаблона, для второй производной выберем
трехточечный шаблон (![]() ).
).
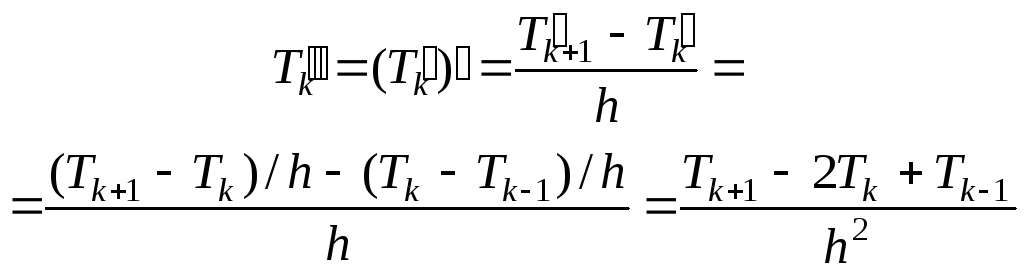 (11)
(11)
Пользуясь разложением
в ряд Тейлора функции
![]() (6), получим, что порядок аппроксимации
в этом случае равен двум, так как:
(6), получим, что порядок аппроксимации
в этом случае равен двум, так как:
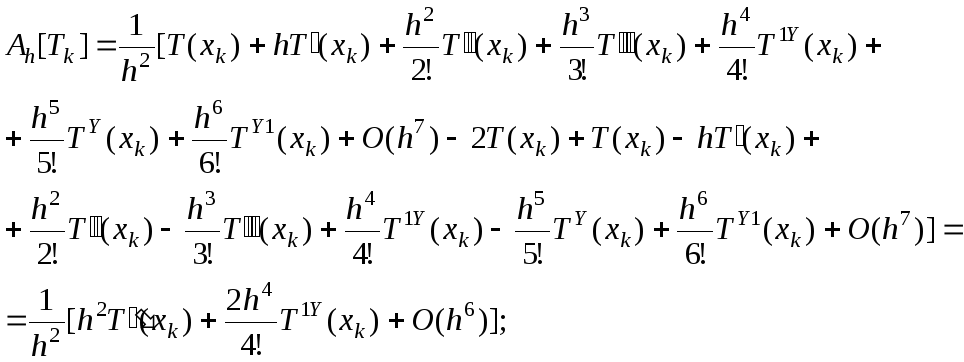
![]()
Рассмотрим оператор одномерного уравнения теплопроводности
![]() (12)
(12)
в области
![]() ,
предполагая, что функция температуры
непрерывна вместе со своими производными
до четвертого порядка по переменнойx
и до второго порядка производной по
времени
,
предполагая, что функция температуры
непрерывна вместе со своими производными
до четвертого порядка по переменнойx
и до второго порядка производной по
времени
![]() .
Область непрерывного изменения аргумента
заменим сеточной областью
.
Область непрерывного изменения аргумента
заменим сеточной областью
![]() ,
,
Аппроксимируем производную по времени правым разностным соотношением
![]() ,
(13)
,
(13)
а для второй производной по переменной x запишем разностное соотношение (11) на временном слое i:
![]() (14)
(14)
или на временном слое i+1
![]() .
(15)
.
(15)
В соответствии с этим можно рассмотреть две различных аппроксимации оператора (12) на шаблонах, приведенных на рис.6
![]() (16)
(16)
![]() (17)
(17)
Погрешность локальной аппроксимации оператора (12) разностными операторами (16),(17) будет равна соответственно

Оператор (12) можно аппроксимировать и на шеститочечном шаблоне, образовав линейную комбинацию уравнений (16), (17):
![]() (18)
(18)
Оценим порядок локальной аппроксимации оператора (12) разностным оператором (18)
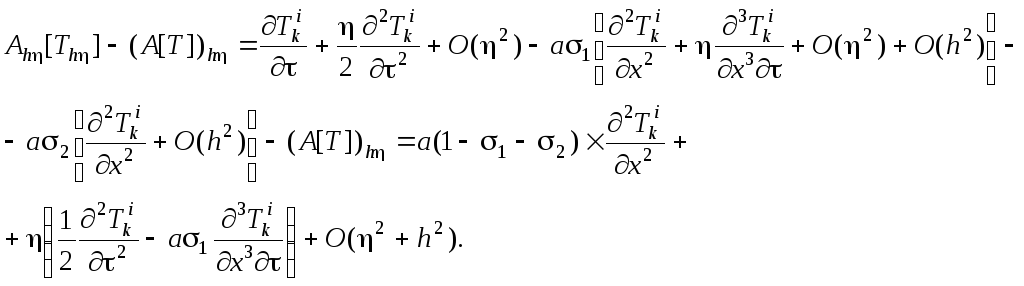
Если предположить,
что
![]() ,
то
,
то![]() При
При
![]()
![]() Т.е. вэтом
случае оператор A[T]
аппроксимируется со вторым порядком
точности по
Т.е. вэтом
случае оператор A[T]
аппроксимируется со вторым порядком
точности по
![]() .
.
Метод интегральных тождеств. Интегро-интерполяционныи метод. При численном решении краевых задач естественно потребовать, чтобы для построенной разностной схемы выполнялись основные законы сохранения субстанции (теплоты, энергии, массы и т.п.), положенные в основу при постановке краевой задачи в дифференциальной форме. Разностные схемы, для которых удовлетворяется это требование, называются консервативными; схемы, в которых нарушаются законы сохранения, - неконсервативными. А. Н. Тихоновым и А. А. Самарским предложен один из наиболее эффективных методов построения консервативных разностных схем – интегро-интерполяционный.
Суть метода состоит в следующем. После выбора шаблона область измене-ния независимых переменных разбивается на элементарные ячейки, связанные с шаблоном. Затем исходное дифференциальное уравнение интегрируют по ячейке и приходят с помощью формул векторного анализа к интегральным соотношениям, выражающим законы сохранения для этой элементарной ячейки. Интегралы и производные, входящие в эти соотношения, заменяются затем разностными отношениями так, чтобы не нарушались законы сохранения. 'Поскольку разностные отношения могут быть взяты не единственным образом, то можно получить различные разностные схемы. В качестве примера рассмотрим уравнение теплопроводности с переменной теплопроводностью
![]() (1)
(1)
Раскроем (1):
![]()
На первый взгляд для получения аппроксимаций второго порядка естественно произвести замены
![]()
тогда получим схему
![]() (2)
(2)
![]()
Решение по такой разностной схеме приводит к неверному результату. Решение расходится. Математически это обозначает накопление ошибки, с физической – не выполнение закона сохранения энергии (возникновение дополнительных источников притока или стока тепла). Это пример неконсервативной схемы.
При написании разностных схем следует добиваться того, чтобы последние выражали на сетке соответствующие законы сохранения, в данном случае – закон сохранения энергии (консервативные схемы). Для написания консервативной схемы используем уравнение баланса, записанного для элементарных объемов (ячеек) сеточной области. Входящие в уравнение баланса интегралы и производные заменим приближенными разностными соотношениями.
Рассмотрим более сложное уравнение
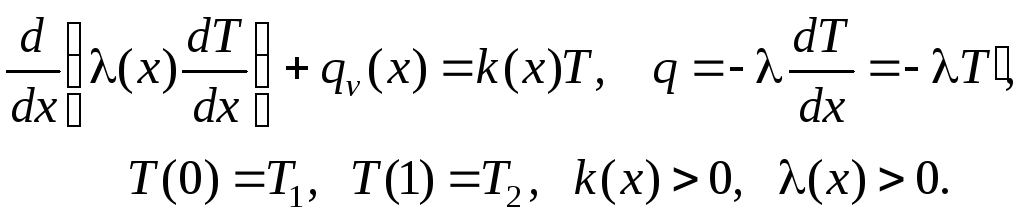 (3)
(3)
Это уравнение
описывает стационарное распределение
температуры в стержне
![]()
Запишем уравнение
баланса тепла на отрезке
![]() .
Для этого проинтегрируем уравнение (3)
в пределах этого отрезка:
.
Для этого проинтегрируем уравнение (3)
в пределах этого отрезка:
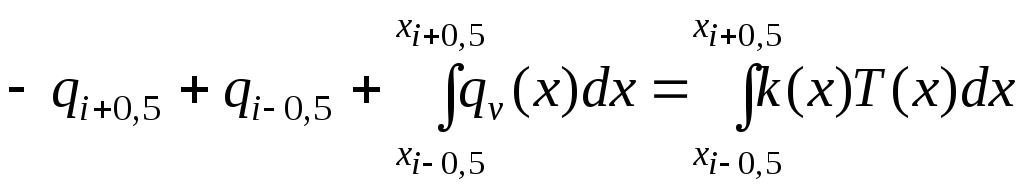 (4)
(4)
![]() - количество тепла
втекающего через сечение
- количество тепла
втекающего через сечение
![]() на отрезке
на отрезке![]() ,
,![]() - количество тепла
вытекающего через сечение
- количество тепла
вытекающего через сечение
![]() на том же отрезке,
на том же отрезке, - количество тепла
выделившегося на отрезке
- количество тепла
выделившегося на отрезке
![]() за счет распределенных с плотностью
за счет распределенных с плотностью![]() источников тепла,
источников тепла,
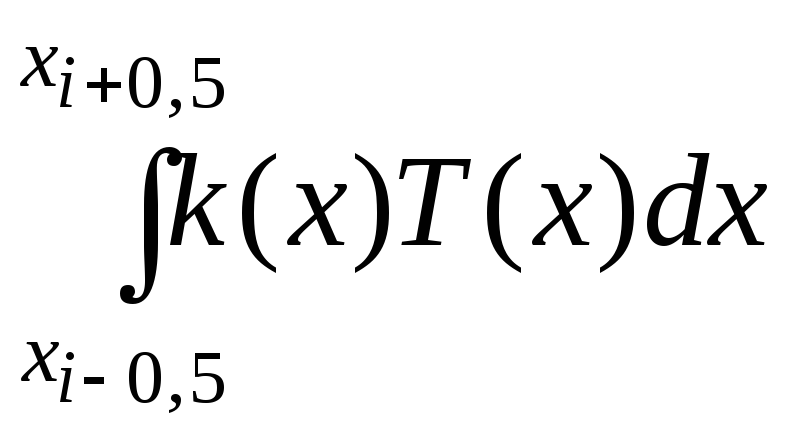 -количество тепла
отданного внешней среде за счет
теплообмена на боковой поверхности.
-количество тепла
отданного внешней среде за счет
теплообмена на боковой поверхности.
Пусть на отрезке
![]()
![]() тогда
тогда
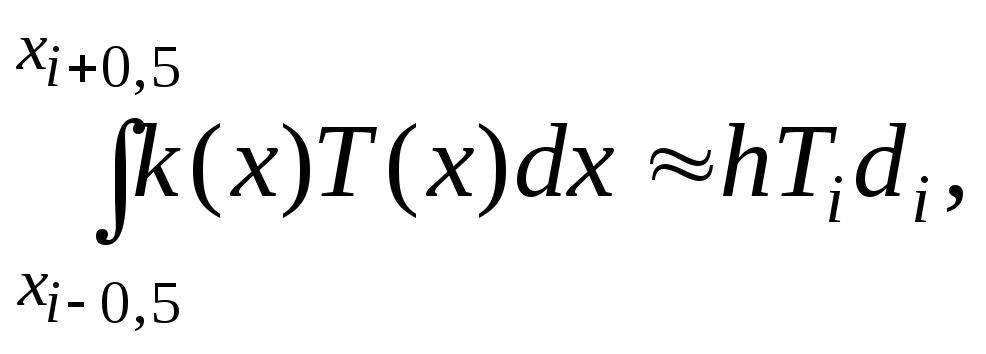

Т.е.
![]() - среднее значениеk(x)
на отрезке
- среднее значениеk(x)
на отрезке
![]() ,
длинойh.
,
длинойh.
Проинтегрируем
равенство
![]() на отрезке
на отрезке![]()

пусть на отрезке
![]()
![]() ,
тогда
,
тогда
 ,
,
где
 ,
,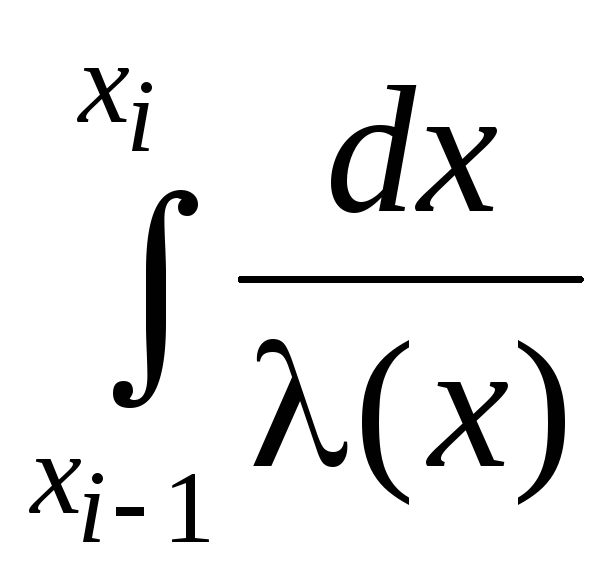 -тепловое
сопротивление отрезка
-тепловое
сопротивление отрезка
![]() ,
найдем
,
найдем![]()
![]() (5)
(5)
Рассмотрим отрезок
![]() и проинтегрируем на нем выражение
и проинтегрируем на нем выражение![]() ,
получим:
,
получим:
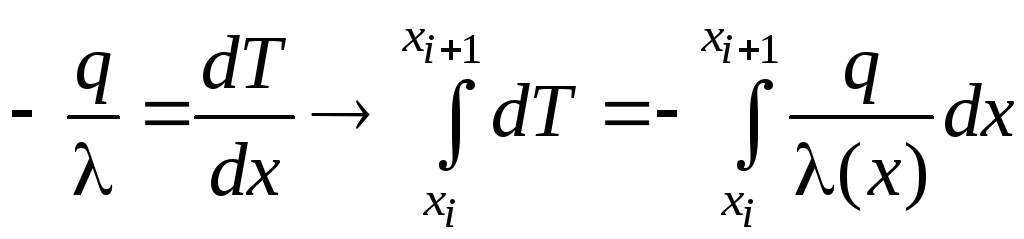 .
.
Пусть
![]() на рассматриваемом отрезке
на рассматриваемом отрезке![]() ,
тогда
,
тогда
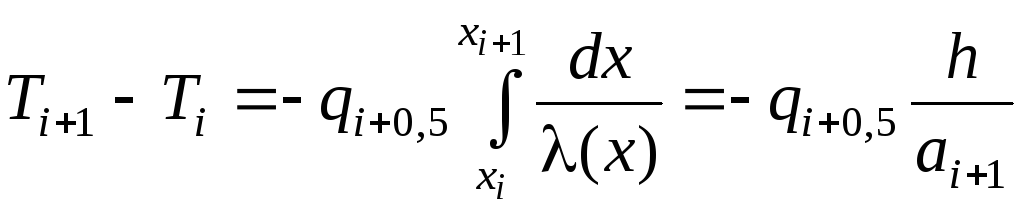
![]() (6)
(6)
где
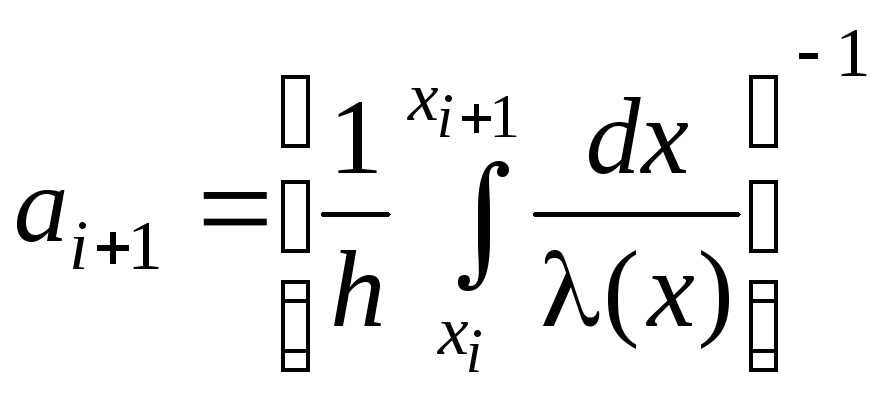 .
Подставим в выражение (4) найденные
величины (5) и (6)
.
Подставим в выражение (4) найденные
величины (5) и (6)
![]() (7)
(7)
(7) – консервативная разностная схема
Таким образом, одним из преимуществ интегро-интерполяционного метода является возможность его применения для уравнений с разрывными коэффициентами, так как интегральная запись закона сохранении субстанции позволяет выделить из всех математически допустимых решений краевой задачи именно то, которое представляет физически правильное обобщенное решение.
Устойчивость и сходимость разностных схем
Пусть требуется
найти решение
![]() краевой задачи теплопроводности:
краевой задачи теплопроводности:
![]() (1)
(1)
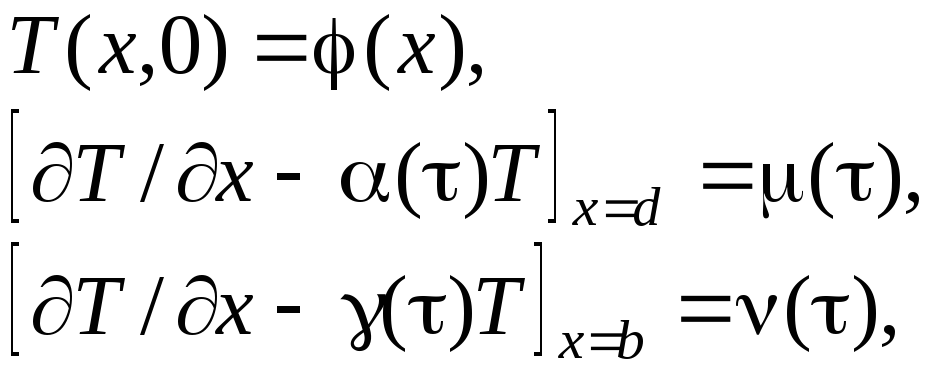 (2)
(2)
где
![]() - заданные функции переменной
- заданные функции переменной![]() .
.
Введем прямоугольную
сетку узлов
![]() ,
,![]() ,
где
,
где![]() .
С помощью метода разностной аппроксимации
запишем три варианта разностной схемы
для уравнения (1), при этом вместо индекса
времениi
будем
применять более удобные обозначения:
.
С помощью метода разностной аппроксимации
запишем три варианта разностной схемы
для уравнения (1), при этом вместо индекса
времениi
будем
применять более удобные обозначения:
![]()
Тогда, варьируя
аппроксимацию производной
![]() ,
имеем
,
имеем
вариант 1
![]() (3)
(3)
вариант 2
![]() (4)
(4)
вариант 3
![]() (5)
(5)
Так как число неизвестных в уравнениях (3)-(5) больше, чем число уравнений, то к каждому из выражений необходимо присоединить начальные и граничные условия, записанные в разностном виде:
![]() (6)
(6)
Обозначим
![]() и представим уравнения (3)-(5) в следующей
форме:
и представим уравнения (3)-(5) в следующей
форме:
вариант 1
![]() (7)
(7)
вариант 2
![]() (8)
(8)
вариант 3
![]() (9)
(9)
а краевые условия в таком виде:
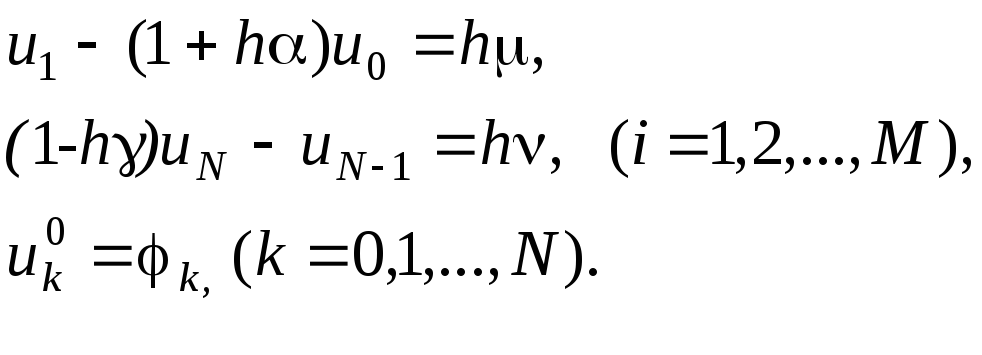 (10)
(10)
Можно показать,
что уравнения (7),(8) аппроксимируют
уравнение (1) с порядком точности
![]() ,
а уравнение (9) – с порядком
,
а уравнение (9) – с порядком![]() .
Порядок аппроксимации краевых условий
(2) уравнениями (6) имеет первый порядок
относительноh.
Поэтому разностные схемы (7),(10); (8),(10);
(9),(10) имеют по пространственной переменной
порядок O(h).
.
Порядок аппроксимации краевых условий
(2) уравнениями (6) имеет первый порядок
относительноh.
Поэтому разностные схемы (7),(10); (8),(10);
(9),(10) имеют по пространственной переменной
порядок O(h).
Какую схему
целесообразнее использовать для
получения приближенного решения и какое
соотношение между шагами
![]() нужно брать? С точки зрения численного
процесса, приводящего к искомому решению,
наиболее просты уравнения (7) и (9).
нужно брать? С точки зрения численного
процесса, приводящего к искомому решению,
наиболее просты уравнения (7) и (9).
Разностные схемы,
позволяющие вычислять значение искомой
функции
![]() на (i+1)-м
временном слое непосредственно по
известным значениям функции на слоях
с номерами
на (i+1)-м
временном слое непосредственно по
известным значениям функции на слоях
с номерами
![]() ,
называютсяявными.
При нахождении приближенного решения
по схеме (8) для вычисления
,
называютсяявными.
При нахождении приближенного решения
по схеме (8) для вычисления
![]() наi-м
временном слое необходимо решить систему
N-1
или
N+1
линейных алгебраических уравнений,
т.е. неизвестные выражены неявно. Такие
разностные схемы называют неявными.
В Общем случае все разностные схемы по
этому принципу (как выражены неизвестные)
делятся на явные и неявные разностные
схемы. Явные схемы имеют несомненное
преимущество перед неявными в простоте
организации вычислений. Однако большинство
явных схем являются условно устойчивыми
и это снижает их эффективность. Условная
устойчивость означает, что не для всех
соотношений шагов по времени и координате
решение будет сходиться к истинному
результату. Отличительной особенностью
явных схем является то, что при их
использовании должно соблюдаться
некоторое условие, обеспечивающее
сходимость и устойчивость метода, в
противном случае будут накапливаться
ошибки в ходе вычислений. Для каждого
вида уравнений проводится анализ
устойчивости и определяется критерий
сходимости (если это возможно сделать).
Уравнению
наi-м
временном слое необходимо решить систему
N-1
или
N+1
линейных алгебраических уравнений,
т.е. неизвестные выражены неявно. Такие
разностные схемы называют неявными.
В Общем случае все разностные схемы по
этому принципу (как выражены неизвестные)
делятся на явные и неявные разностные
схемы. Явные схемы имеют несомненное
преимущество перед неявными в простоте
организации вычислений. Однако большинство
явных схем являются условно устойчивыми
и это снижает их эффективность. Условная
устойчивость означает, что не для всех
соотношений шагов по времени и координате
решение будет сходиться к истинному
результату. Отличительной особенностью
явных схем является то, что при их
использовании должно соблюдаться
некоторое условие, обеспечивающее
сходимость и устойчивость метода, в
противном случае будут накапливаться
ошибки в ходе вычислений. Для каждого
вида уравнений проводится анализ
устойчивости и определяется критерий
сходимости (если это возможно сделать).
Уравнению
![]() с использованием явной разностной схемы
соответствует критерий
с использованием явной разностной схемы
соответствует критерий
![]() .
(*)
.
(*)
Этим условием накладывается довольно серьезное ограничение на шаг по времени.
Неявные методы, например схема (8) имеют безусловную устойчивость, т.е. шаги по времени и координате могут быть любыми. Однако, при вычислении приближенного решения по этим схемам на каждом следующем моменте времени требуется решать систему линейных алгебраических уравнений со многими неизвестными, что требует привлечение специальных методов и машинного времени.
При решении задачи с помощью третьей схемы (10), после того, как вычислены значения решения на первом временном слое, организация счета также проста, как и в схеме (7). Поэтому эта схема также относится к явным разностным схемам. Значения решения на первом слое можно получить с помощью разложения в ряд Тейлора искомой функции:
![]() (11)
(11)
Используя основное дифференциальное уравнение теплопроводности, получим, что
![]() ,
(12)
,
(12)
и подставим (12) в (11), тогда
![]()
Таким образом, на
первый взгляд кажется, что целесообразней
всего вести расчет задачи по схеме (9)
(вариант 3); с точки зрения аппроксимации
это уравнение лучше по сравнению с двумя
первыми. Расчет поля температур для
задачи (1),(2) по трем представленным
вариантам, когда
![]() ,
,![]() показал, что расчеты по второму варианту
дают качественно приемлемые результаты,
а расчеты по 1и 3 вариантам приводят к
абсурдным результатам при
показал, что расчеты по второму варианту
дают качественно приемлемые результаты,
а расчеты по 1и 3 вариантам приводят к
абсурдным результатам при![]() ,
т.е.
,
т.е.![]() уже на временном слое
уже на временном слое![]() .
В случае 1 и 3 вариантов разностной схемы
встречаемся с явлением, которое называетсянеустойчивостью
разностной схемы. Суть этого явления
заключается в том, что при счете по
неустойчивой схеме вычислительные
погрешности, избежать которых невозможно
хотя бы из-за округления чисел, появляясь
на некотором временном слое, быстро
растут и вскоре приводят к неприемлемым
результатам. Т.е. схемы, которые в процессе
счета усиливают начальные погрешности.
.
В случае 1 и 3 вариантов разностной схемы
встречаемся с явлением, которое называетсянеустойчивостью
разностной схемы. Суть этого явления
заключается в том, что при счете по
неустойчивой схеме вычислительные
погрешности, избежать которых невозможно
хотя бы из-за округления чисел, появляясь
на некотором временном слое, быстро
растут и вскоре приводят к неприемлемым
результатам. Т.е. схемы, которые в процессе
счета усиливают начальные погрешности.
Если же возникающие в процессе расчетов вычислительные погрешности имеют тенденцию убывать (по крайней мере, не возрастают), то разностная схема называется устойчивой. Т.е. малому изменению входных данных соответствует малое изменение решения.
При уменьшении
шага по времени
![]() решения, полученные по 1 и 2-му варианту
оказались близки между собой. Счет по
третьему варианту неустойчив. Если при
достаточно малых шагах по разным
переменным для устойчивости разностной
схемы шаги должны удовлетворять
дополнительным соотношениям, то
устойчивость называетсяусловной;
1-й вариант разностной схемы относится
к условно устойчивым схемам при выполнении
условия (8).
решения, полученные по 1 и 2-му варианту
оказались близки между собой. Счет по
третьему варианту неустойчив. Если при
достаточно малых шагах по разным
переменным для устойчивости разностной
схемы шаги должны удовлетворять
дополнительным соотношениям, то
устойчивость называетсяусловной;
1-й вариант разностной схемы относится
к условно устойчивым схемам при выполнении
условия (8).
Разностные схемы,
которые при достаточно мелких шагах по
независимым переменным и любом сколь
угодно малом
![]() неустойчивы (вариант 3), называютсяабсолютно
неустойчивыми.
неустойчивы (вариант 3), называютсяабсолютно
неустойчивыми.
Если же факт устойчивости имеет место при любом соотношении шагов по различным переменным, лишь бы они были достаточно малы, то схема называется безусловно устойчивой (вариант 2).
В общем случае разностное решение или его устойчивость может зависеть от правой части, граничных условий и начальных условий. Поэтому различают три вида устойчивости : по правой части, граничным условиям и начальному условию. Для исследования устойчивости разностной схемы используют различные методы такие, как разделение переменных, принцип максимума, разложение в ряд Фурье и т.д.
Экономичные схемы
Численные
исследования нестационарных задач в
дух и трехмерных пространствах значительно
сложнее задач в одномерной постановке.
При этом не вызывает затруднений в
построении самого разностного аналога
краевых задач. Однако число неизвестных
в разностных схемах в многомерных
случаях значительно возрастает. Если
выбрать шаг h
по всем пространственным переменным,
то на каждом временном шаге необходимо
решать систему алгебраических уравнений
с
![]() неизвестными , гдеp
–число измерений. В связи с этим
значительно возрастает объем физических
операций, необходимых для решения
системы разностных уравнений. Так, если
в прямоугольнике (
неизвестными , гдеp
–число измерений. В связи с этим
значительно возрастает объем физических
операций, необходимых для решения
системы разностных уравнений. Так, если
в прямоугольнике (![]() )
задана краевая задача с граничными
условиями первого рода
)
задана краевая задача с граничными
условиями первого рода
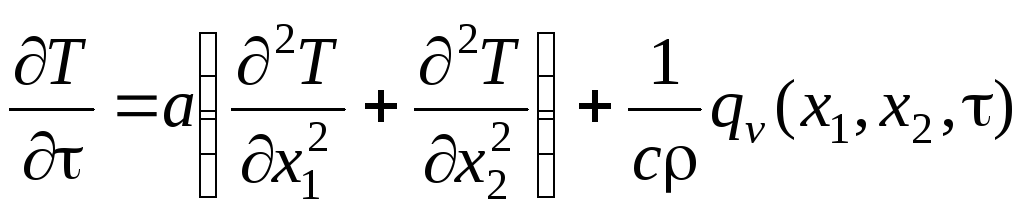 ,
,
![]() ,
,![]() (1)
(1)
![]() (2)
(2)
![]() ;
;
![]() (3)
(3)
![]()
![]()
![]() (4)
(4)
то на прямоугольной
сетке
![]() ,
выбрав шаблон, изображенный на рис.7,
можно составить неявную разностную
двухслойную схему с весами:
,
выбрав шаблон, изображенный на рис.7,
можно составить неявную разностную
двухслойную схему с весами:
![]() (5)
(5)
![]() (6)
(6)
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
здесь введены разностные операторы
![]()
![]() (9)
(9)
Посмотрим с точки
зрения объема вычислительной работы
на полученную схему, полагая, что число
по каждой переменной равно N.
При
![]() схема (5) явная и для вычисления
схема (5) явная и для вычисления![]() по известным значениям
по известным значениям![]() требуется выполнить общее число действий,
пропорциональное числу узлов сетки
требуется выполнить общее число действий,
пропорциональное числу узлов сетки![]() .
Но явная схема устойчива при жестком
ограничении на шаг по времени
.
Но явная схема устойчива при жестком
ограничении на шаг по времени
![]() .
.
Такое дробление
шага по времени не связано с требованиями
по точности решения и приводит к
неоправданно большому объему вычислений
![]() ,
гдеp-
количество измерений.
,
гдеp-
количество измерений.
При
![]() схема (5) неявная. Она устойчива при любых
шагах
схема (5) неявная. Она устойчива при любых
шагах![]() иh.
Если
иh.
Если
![]() ,
то на каждом временном слое необходимо
решить систему
,
то на каждом временном слое необходимо
решить систему![]() уравнений. Для решения этой системы
методом Гаусса необходимо провести
уравнений. Для решения этой системы
методом Гаусса необходимо провести![]() действий. При
действий. При![]() расчет по неявной схеме даже менее
эффективен, чем по явной.
расчет по неявной схеме даже менее
эффективен, чем по явной.
Таким образом, явные и неявные схемы имеют свои положительные качества. Явная – объем вычислений пропорционален числу узлов разностной схемы, неявная – безусловно устойчива. Разностные схемы, сочетающие эти положительные свойства, называются экономичными.
Наибольшее распространение получили разностные схемы, основанные на методе дробных шагов по временной переменной. Экономичность решения задач с помощью разностных схем, основанных на методе дробных шагов, достигается сведением многомерной задачи к решению последовательности одномерных, для решения которых может быть использован эффективный метод прогонки.
Метод переменных направлений.
Метод переменных направлений является одним из наилучших для решения двумерных краевых задач. Для построения разностного аналога уравнения(1) введем сетку с координатами узлов
![]()
![]()
![]()
Выберем на сетке
шаблон, содержащий полуцелый слой
![]() ,
рис.8, и составим на нем следующую
разностную схему:
,
рис.8, и составим на нем следующую
разностную схему:
![]() (10)
(10)
![]() (11)
(11)
где разностные операторы определены выражением (9).
Из уравнения (10),
(11) видно, что переход от j-го
временного слоя к j+1-му
временному слою осуществляется в два
шага по времени. Сначала с помощью
уравнения (10) вычисляют промежуточные
значения искомой функции
![]() .
Уравнение (10) содержит три неизвестных
.
Уравнение (10) содержит три неизвестных![]() ,
,![]() ,
,![]() ;
остальные значенияu
определены на исходном слое, т.е. уравнение
(10) неявно по координате
;
остальные значенияu
определены на исходном слое, т.е. уравнение
(10) неявно по координате
![]() и явно - по
и явно - по![]() .
При любом фиксированномm
уравнение (10) может быть решено методом
одномерной прогонки по направлению
.
При любом фиксированномm
уравнение (10) может быть решено методом
одномерной прогонки по направлению
![]() .
Далее, схема (11), содержащая неизвестные
.
Далее, схема (11), содержащая неизвестные![]() ,
,![]() ,
,![]() ,
неявна по направлению
,
неявна по направлению![]() и явна по направлению
и явна по направлению![]() .
Поэтому решение системы (11) можно получить
одномерной прогонкой по направлению
.
Поэтому решение системы (11) можно получить
одномерной прогонкой по направлению![]() .
Таким образом, переход сj
–го временного
слоя на j+1-
й совершается с помощью одномерного
метода прогонки вначале в продольном
направлении, а затем в поперечном. Этим
обусловлено название метода.
.
Таким образом, переход сj
–го временного
слоя на j+1-
й совершается с помощью одномерного
метода прогонки вначале в продольном
направлении, а затем в поперечном. Этим
обусловлено название метода.
Рассмотрим вопрос аппроксимации граничных условий (3), (4). Постановка разностных граничных условий на целом слое не вызывает затруднений:
![]()
![]() ,
,
![]() . (14)
. (14)
Для прогонки по
направлению
![]() необходимо задавать значение
необходимо задавать значение![]() приn=0
и n=N.
Однако задавать
приn=0
и n=N.
Однако задавать
![]() и
и![]() нецелесообразно, так как значения
нецелесообразно, так как значения![]() не вполне соответствуют моменту
не вполне соответствуют моменту![]() ,
при этом вносилась бы погрешность.
Поэтому при аппроксимации граничных
условий на полуцелом слое определяют
промежуточное значение
,
при этом вносилась бы погрешность.
Поэтому при аппроксимации граничных
условий на полуцелом слое определяют
промежуточное значение![]() ,
вычитая уравнение (11) из уравнения (10)
,
вычитая уравнение (11) из уравнения (10)
![]() (12)
(12)
и записывая разность в узлах n=0 и n=N :
![]()
![]() (15)
(15)
![]()
Выбрав граничные условия в виде (14), (15), обеспечим второй порядок аппроксимации граничных условий (3) , (4) по времени.
Метод установления
Рассмотренные
экономичные разностные схемы справедливы
для нестационарных уравнений. Однако
в ряде случаев удается их применять для
решения стационарных задач. Известно
из математической физики, что решение
стационарного уравнения можно
рассматривать как установившееся
решение соответствующего нестационарного
уравнения при
![]() .
При этом сам процесс установления роли
не играет (как идет процесс установления
и величины промежуточных значений
искомой функции), зачастую лишен
физического смысла, а величина
.
При этом сам процесс установления роли
не играет (как идет процесс установления
и величины промежуточных значений
искомой функции), зачастую лишен
физического смысла, а величина![]() является параметром разностной схемы
(не является временем). Счет ведется до
выполнения условия
является параметром разностной схемы
(не является временем). Счет ведется до
выполнения условия
![]() .
.
Методы решения сеточных уравнений Система линейных алгебраических уравнений
Задачи решения систем уравнений появляются практически во всех областях прикладной математики. В некоторых случаях системы уравнений составляют ту задачу, которую нужно решать, в других – некоторая задача сводится к системе линейных алгебраических уравнений.
Будем рассматривать систему из n уравнений с n неизвестными. Каждый член уравнения содержит только одно неизвестное и каждое неизвестное входит в уравнение в первой степени. Такая система уравнений называется линейной.
В случае дух неизвестных каждое уравнение изображается линией; трех неизвестных –плоскостью; для 4-х и более неизвестных – гиперплоскостью. Искомое решение системы уравнений представляет собой набор значений неизвестных, удовлетворяющих одновременно всем уравнениям.
На вопрос о разрешимости рассматриваемой системы уравнений существует тир возможных ответа:
решение системы существует и является единственным, например
 (1)
(1)
Решением этой системы является : x=1;y=2 – координаты точки пересечения двух прямых.
Никакие другие значения неизвестных не удовлетворяют одновременно два уравнения.
Система уравнений не имеет решения, например
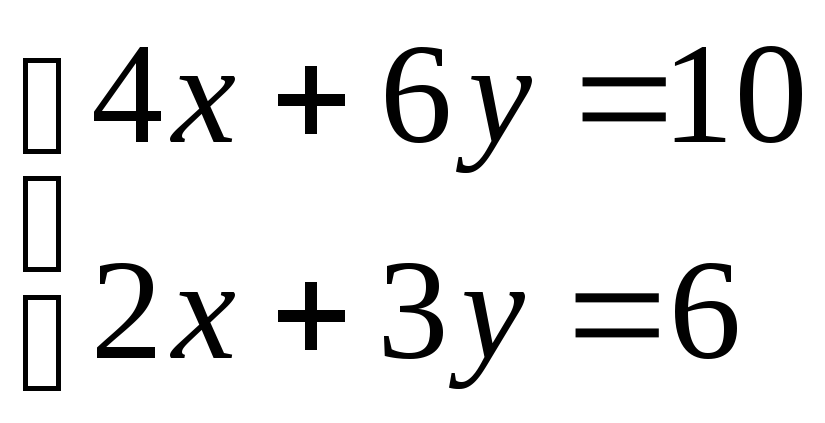 (2)
(2)
Линии соответствующие приведенным уравнениям параллельны друг другу и, следовательно, не имеют точек пересечения.
Система уравнений имеет бесконечное множество решений:
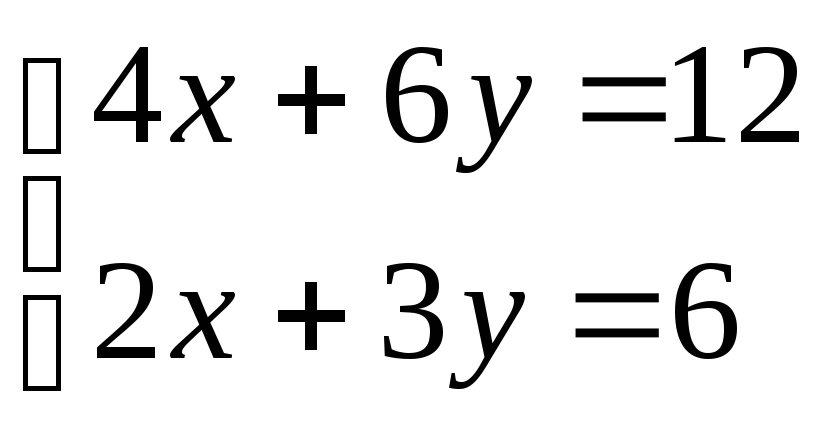 (3)
(3)
В этом случае оба уравнения описывают одну и ту же прямую. Поскольку прямые совпадают, то любая точка, лежащая на одной прямой будет решением системы.
Системы уравнений (2) и (3) называются вырожденными (детерминанты равны нулю). На практике встречаются случаи, когда системы являются плохо обусловленными, для которых затруднительно бывает отыскать решение, например:
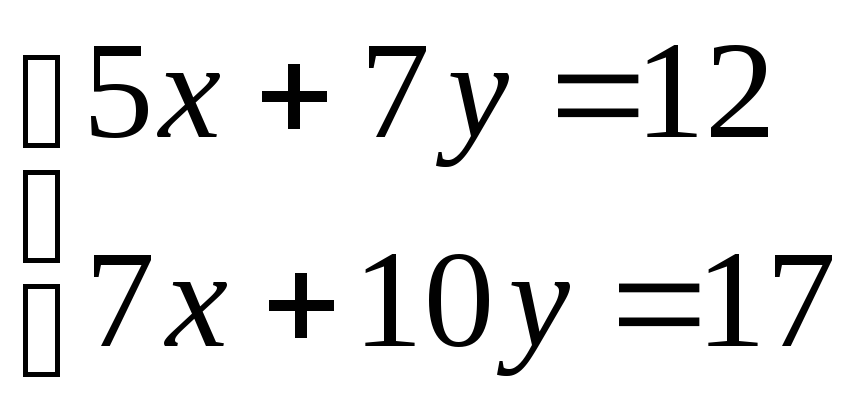 (4)
(4)
Прямые в системе (4) близки друг к другу. Решением этой системы являются значения x=1, y=1, но при значениях неизвестных - x=2.415, y=0 получим
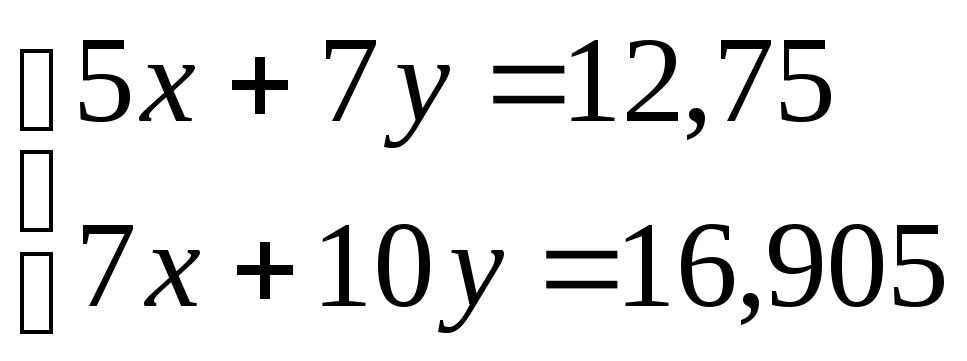 (5)
(5)
хотя точка (2.475,0) не принадлежит ни одной прямой. В этом случае найти численное решение трудно, а точность сомнительна. Система из 3–х и более уравнений может оказаться плохо обусловленной даже, если ни одна из плоскостей не располагается почти параллельно к другой плоскости.
Методы численного решения систем линейных уравнений подразделяются на два типа: прямые (конечные) и итерационные (бесконечные). Прямые методы могут в принципе дать точное решение (с точностью до ошибки округления), если оно существует, с помощью конечного числа арифметических операций. Итерационные методы требуют бесконечного числа арифметических операций, приводящих к точному решению. Т.е. при использовании итерационных методов появляется ошибка ограничения, отсутствующая в прямых методах. Из последнего не следует, что прямые методы всегда наиболее точные. Все зависит от ошибок округления и ограничения.
