
Прямые методы
Метод Гаусса (метод исключения)
Рассмотрим систему из трех уравнений с тремя неизвестными:
 (*)
(*)
Введем множитель
![]() , умножим первое уравнение на
, умножим первое уравнение на![]() и вычтем его из уравнения (2):
и вычтем его из уравнения (2):
![]() ,
,
получим: первая скобка равна нулю, а другие переобозначим, тогда имеем
![]() (4)
(4)
Заменим второе
уравнение системы (*) на полученное (4).
Введем множитель
![]() ,
умножим уравнение (1) на
,
умножим уравнение (1) на![]() и вычтем из уравнения (3)
и вычтем из уравнения (3)
![]()
Заменим уравнение (3) на полученное , будем иметь систему:

Новая система
уравнений полностью эквивалентна
системе (*) с тем преимуществом, что в
двух последних уравнениях нет члена с
![]() .
Теперь можно найти
.
Теперь можно найти![]() ,
а
,
а![]() получится в результате подстановки
найденных значений в (1). Исключим теперь
получится в результате подстановки
найденных значений в (1). Исключим теперь![]() в уравнении (5).
в уравнении (5).
Введем множитель
![]() и проделаем аналогичную процедуру:
и проделаем аналогичную процедуру:
![]()
![]() .
.
Получим новую эквивалентную систему:

Полученная система
называется треугольной. Теперь процесс
нахождения неизвестных значительно
упрощается. Сначала определяется
![]() из уравнения (6), его значение подставляется
в (4) и определяется
из уравнения (6), его значение подставляется
в (4) и определяется![]() ,
затем из уравнения (1) по уже известным
,
затем из уравнения (1) по уже известным![]() находится последнее неизвестное
находится последнее неизвестное![]() :
:
![]()
![]()
![]()
В том случае, когда
![]() ,
система уравнений является вырожденной.
,
система уравнений является вырожденной.
ПРИМЕР:

![]() =2;
(2-2)x+(3-2)y+z=4;
=2;
(2-2)x+(3-2)y+z=4;
![]() y-z=1
y-z=1

![]() ;
(-2+2)y+(-2-2)z=-6+2;
;
(-2+2)y+(-2-2)z=-6+2;
![]() -4z=-4
-4z=-4

![]() z=1;
y=2;
x=1.
z=1;
y=2;
x=1.
Т.о., найдено точное решение системы уравнений с помощью конечного числа арифметических операций. В данном случае ошибки округления отсутствовали.
Обобщим рассматриваемый
метод решения на систему n
уравнений с n
неизвестными. Обозначим неизвестные
![]() .
Запишем уравнения в следующем виде:
.
Запишем уравнения в следующем виде:

Введем (n-1)
множителей
![]() (i=1…n)
(i=1…n)
![]()
Вычтим из каждого
i-уравнения
первое уравнение, умноженное на
![]() .
Обозначим:
.
Обозначим:
![]()
где i=2,…n, j=1,…n.
Преобразованная система запишется в следующем виде:

Аналогичным образом
можно исключить из (n-2)
уравнений неизвестное
![]() ,
а затем из (n-3)
уравнений
,
а затем из (n-3)
уравнений
![]() и т.д. На некоторомk-
этапе при исключении неизвестного
и т.д. На некоторомk-
этапе при исключении неизвестного
![]() имеем множители:
имеем множители:
 i=k+1,…,n
i=k+1,…,n
Новые коэффициенты на k- шаге будут

i=k+1,…,n; j=k,…,n;
Индекс k=1,…,n-1, при k=n-1 исключается (n-1) – ый элемент.
Окончательно треугольная система уравнений имеет вид:
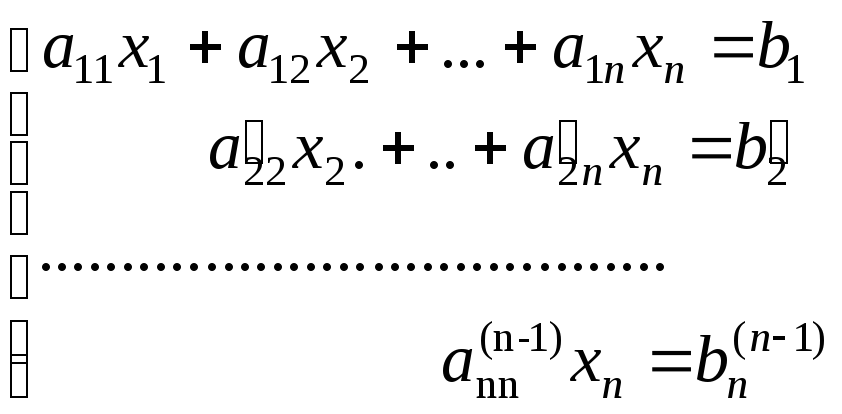
Индексы i,j,k обозначают следующее: k – номер того уравнения, которое вычитается из остальных, а также номер того неизвестного, которое исключается из оставшихся (n-k) уравнений; i- номер того уравнения, из которого в данный момент исключается неизвестное; j- номер столбца.
Для нахождения значений неизвестных производят обратную подстановку:

Метод прогонки
Метод прогонки относится к прямым методам решения систем линейных алгебраических уравнений и является модификацией метода исключения Гаусса для частного случая разряженных систем. К таким системам относятся системы уравнений с трехдиагональной матрицей. К подобным системам часто приходят при решении большого класса инженерных задач в том числе и в технологии кабельного производства. Особенно распространены такие системы при численном решении краевых задач в дифференциальной постановке.
Запишем систему уравнений в виде:
 (1)
(1)
На главной диагонали
матрицы этой системы стоят элементы
![]() ,
,
над ней – элементы
![]() ,
под ней -
,
под ней -![]() .
При этом чаще всего
.
При этом чаще всего![]()

Метод прогонки
состоит из двух этапов – прямой прогонки
(аналога прямого хода метода Гаусса) и
обратной прогонки (аналога обратной
прогонки метода Гаусса). На первом этапе
каждое неизвестное выражается через
последующее, то есть
![]() через
через![]() с помощью прогоночных коэффициентов
с помощью прогоночных коэффициентов![]()
![]() i=1,…,n-1
(2)
i=1,…,n-1
(2)
Из первого уравнения системы найдем:
![]() ,
,
или
![]() ,
,
где
![]()
Из второго уравнения
системы выразим
![]() через
через![]() ,
заменяя
,
заменяя![]() по формуле (2):
по формуле (2):
![]()
Отсюда

Аналогично можно вычислить прогоночные коэффициенты для любого номера i:
 (3)
(3)
Обратная прогонка
состоит в последовательном вычислении
неизвестных
![]() .
С начало, как и в методе Гаусса, отыскивается
.
С начало, как и в методе Гаусса, отыскивается![]() .
Для этого рассматривается уравнение
(2) и последнее уравнение системы:
.
Для этого рассматривается уравнение
(2) и последнее уравнение системы:
![]()
Отсюда, исключая
![]() , находим:
, находим:
![]()
Далее, используя
формулу (2) и выражения для прогоночных
коэффициентов (3), последовательно
вычисляем неизвестные
![]() .
Для решения системы линейных уравнений
методом прогонки необходимо выполнение
следующего условия:
.
Для решения системы линейных уравнений
методом прогонки необходимо выполнение
следующего условия:
![]() (4)
(4)
Приведенное условие (4) преобладания диагональных коэффициентов обеспечивает устойчивость метода с точки зрения ошибок (погрешностей) округления. Последнее обстоятельство позволяет использовать метод прогонки для решения больших систем уравнений. Рассматриваемый метод в сравнении с методом Гаусса является более экономичным.
