Задания для отчета по лабораторной работе

1. К вертикальной проволоке длиной l = 5 м и площадью поперечного сечения S = 2 мм² подвешен груз массой m = 5,1 кг. В результате проволока удлинилась на x = 0,6 мм. Найти модуль Юнга материала проволоки.

2. К стальному стержню длиной l = 3 м и диаметром d = 2 см подвешен груз массой m = 2,5 10³ кг. Определить напряжение σ в стержне. Модуль Юнга стали E = 220 ГПа (ГигаПаскаль).

3. По условиям предыдущей задачи определить относительное ε и абсолютное удлинение x стержня.

4. Проволока длиной l = 2 м и диаметром d = 1 мм натянута практически горизонтально. Когда к середине проволоки подвесили груз массой m = 1 кг, проволока растянулась настолько, что точка подвеса опустилась на h = 4 см. Определить модуль Юнга E материала проволоки.

5. Тонкий стержень одним концом закреплен, к другому концу приложен момент силы M = 1 кН м. Определить угол φ закручивания стержня, если постоянная кручения C = 120 кН м /рад.

6. Коэффициент линейного теплового расширения стали равен 12 10^{-6 0}С^-1., модуль Юнга E = 2 10¹² дин/см². Какое давление p необходимо приложить к торцам стального цилиндра, чтобы длина его оставалась неизменной при повышении температуры на 100⁰ С.

7. Стальной канат диаметра 9 мм может выдержать вес неподвижной кабины лифта. Какой диаметр должен иметь канат, если кабина лифта может иметь ускорение до 8 g.

8. Насколько вытягивается стержень из железа (модуль Юнга 220 ГПа), подвешенный за один конец под действием собственного веса?

9. По условиям предыдущей задачи определить, насколько меняется объем стержня.

10. 10.Какую работу A надо совершить, чтобы растянуть на x = 1 мм стальной стержень (E = 220 ГПа) длиной l = 1 м и площадью поперечного сечения S = 1 см².

11. Точка совершает колебания с частотой ω и коэффициентом затухания β. Найти амплитуду скорости точки как функцию времени, если в момент t = 0 амплитуда ее смещения равна a₀.

12. По условиям предыдущей задачи найти амплитуду скорости точки как функцию времени, если в момент t = 0 смещение x(0) = 0 и проекция скорости v_x = v₀.

13. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ₀ = 1,5. Каким будет значение λ, если сопротивление среды увеличить в n = 2 раза?

14. По условиям предыдущей задачи определить, во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?

15. К пружине подвесили груз, и она растянулась на Δx = 9,8 см. Логарифмический декремент затухания λ = 3,1. С каким периодом будет колебаться груз в вертикальном направлении?

16. Амплитуда затухающих колебаний маятник за время t₁ = 5 мин уменьшилась в два раза. За какое время t₂ , считая от начального момента, амплитуда уменьшится в восемь раз?

17. За время t = 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания β.

18. Логарифмический декремент затухания колебаний маятника равен 0.003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза?

19. Амплитуда колебаний маятника длиной l = 1 м за время t = 10 мин уменьшилась в два раза. Определить логарифмический декремент затухания β.

20. Определить период T затухающих колебаний, если период T₀ собственных колебаний системы равен 1 с и логарифмический декремент λ = 0,628.

Приложение I Коэффициенты Стьюдента (при а = 0,95)

п	2	3	4	5	6	7	8	9	10	20	∞
τ(α,n)	12,7	4,3	3,2	2,8	2,6	2,4	2,4	2,3	2,3	2,1	2

Приложение II . Обработка экспериментального графика методом наименьших квадратов

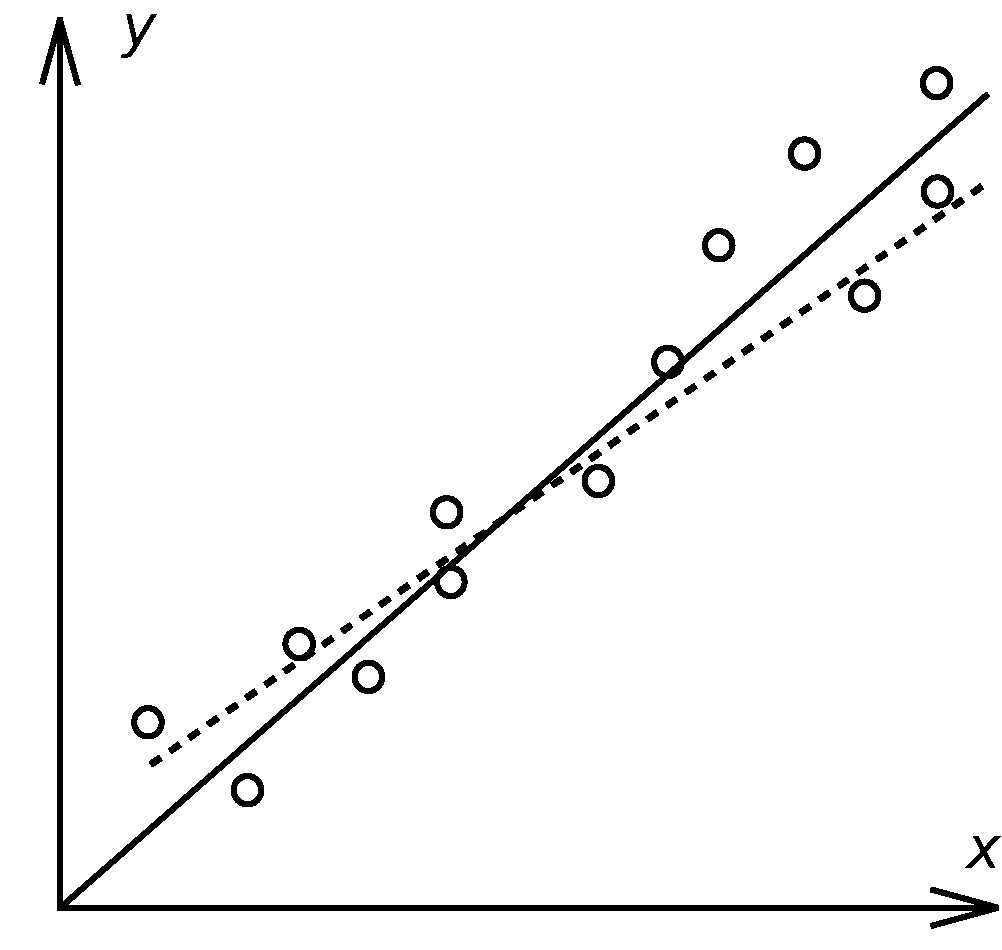
Зависимость измеряемой величины у от условий опыта х может быть найдена графически, если нанести значения х и у на миллиметровую бумагу и построить плавную кривую так, чтобы точки равномерно распределились по обе стороны кривой (рис. 1). Задача состоит в том, чтобы по результатам опытов построить такую кривую у = f(x), относительно которой разброс (отклонения) экспериментальных точек был бы минимальным.

Tеория вероятности показывает, что наилучшее приближение к истинной зависимости у = f(x) дает кривая, построенная методом наименьших квадратов. В этом случае сумма квадратов отклонений экспериментальных значений у_i от кривой у = f(x) будет минимальна. Отсюда и происходит название данного метода обработки результатов эксперимента.

1. Рассмотрим применение метода наименьших квадратов для случая, когда между измеряемыми величинами хиу существует ли-нейная зависимость

Рис. 1 y = bx . (1)

Пусть в результате эксперимента получено п различных значений величины у_i соответствующих различным значениям величины х_i . Найдем коэффициент b, при котором экспериментальные точки у_i будут иметь наименьшие отклонения Δу_i относительно прямой.

Отклонение каждого значения у_i от прямой у = bх будет

y_i - b x_i = Δy_i . (2)

Составим сумму квадратов отклонений:

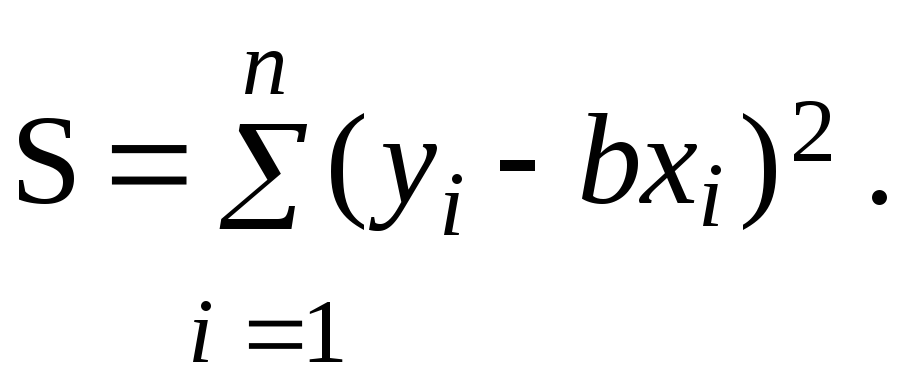(3)

Отклонение (разброс) измеренных значений у_i от функции у = f(x) будет минимальным, если

(4)

Дифференцирование (3) по переменной b (предположив, что все остальные величины постоянны) с учетом (4) дает

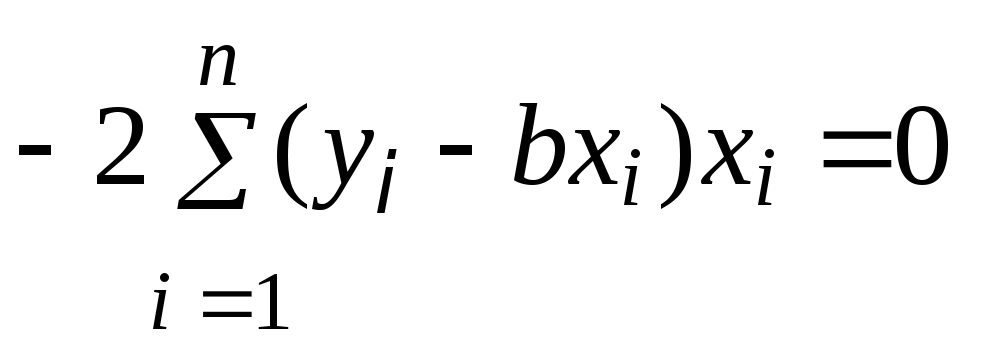или (5)

Отсюда определяем искомый коэффициент b:

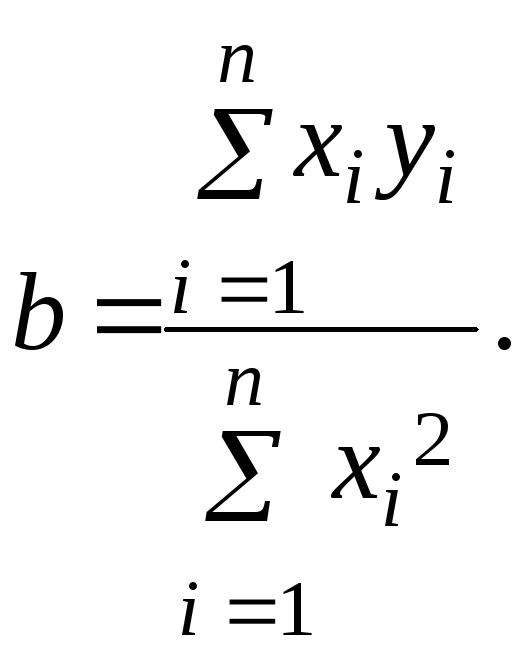(6)

2. В случае линейной зависимости между величинами х и у, которая аппроксимируется прямой, не проходящей через начало координат

у = а + bх , (7)

коэффициенты а и b могут быть вычислены по формулам:

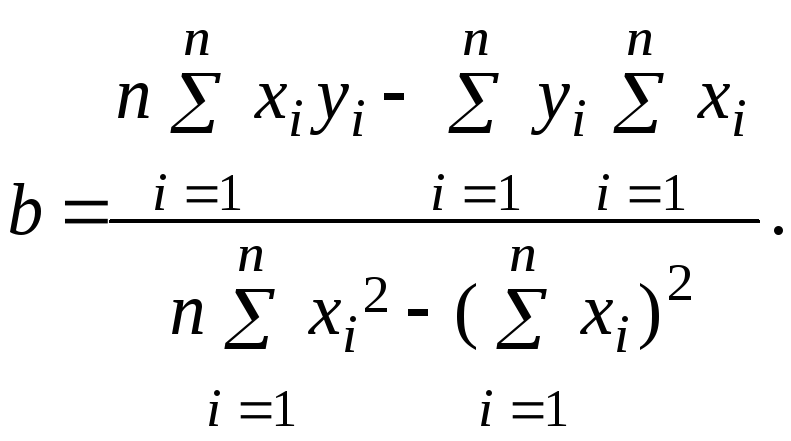
(8)

Пример: предположим, что мы провели эксперимент и получили данные, которые занесли в табл. 1.

Таблица 1

№ измерения i	1	2	3	4	5
xi	1,0	1,9	3,1	4,0	4,9
yi	1,6	2,5	3,0	3,7	4,6

Для упрощения расчетов составим вспомогательную таблицу и заполним ее.

Таблица 2

№ измерения i	xi	yi	xi уi	xi^2
1	1,0	1,6	1,6	1,0
2	1,9	2,5	4,75	3,61
3	3,1	3,0	9,3	9,61
4	4,0	3,7	14,8	16,0
5	4,9	4,6	22,54	24,01
Σ	14,9	15,4	52,99	54,23

Рассчитаем коэффициенты а и b:

Таким образом, уравнение прямой будет выглядеть следующим образом:

у=0,928 + 0,722 х .

Для построения отрезка прямой линии найдем две точки, через которые проходит эта прямая. Первую точку получим при х = 0:

y₁ = 0,928 .

Вторую точку получим, подставив в уравнение прямой значение х, равное, например, 5:

Рис. 2 у₂ = 0,928 + 0,722 · 5 = 4,538 .

На листе миллиметровой бумаги проведем оси координат, причем ось у проведем вертикально, а ось х - горизонтально. Выберем и нанесем на оси коор-

динат масштаб так, чтобы наши экспериментальные точки располагались на графике наилучшим образом - занимали на графике максимальную площадь. Нанесем на график экспериментальные точки и две точки у₁ и у₂, рассчитанные нами (рис. 2). Для обозначения экспериментальных и "теоретических" точек используем разные обозначения (кружки, крестики, треугольники и т. п.).

Через две "теоретических" точки проведем отрезок прямой линии. При правильных расчетах линия пройдет на графике наилучшим образом, так, что экспериментальные точки будут располагаться справа и слева от прямой. Все построения желательно делать карандашом.