24 Волновая функция и уравнение Шредингера. Статический смысл волновой функции.

Уравнение учитывающее волновые и корпускулярные свойства частицы было получено Шредингером в 1926г.

Шредингер сопоставил движение частицы на комплексную функцию координат и времени, которая называется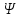функцией, эта функция является решением уравнения Шредингера:

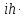
, где 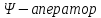Лапласа, который можно

расписать: 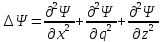;;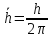 U-потенциальная энергия частицы; Где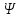- функция координат и времени.

В квантовой физикенельзя точно предсказатькакие либо события, а можно говорить только о вероятностиданного события, вероятность событий и определяет .

1) Вероятность нахождения микрочастицы в объеме dV в момент времени Т :

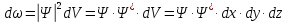
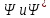-сопряженные функции.

2) Плотность вероятностей нахождения частицы в единице объема:

.

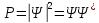3) Волновая функция должна удовлетворять условию:

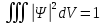
где 3 интеграла расчитываются по всему объему, где может находится частица.

Данное условие означает, что пробывание частицы – достоверное событие с вероятностью 1

25 Уравнение Шредингера для стационарных состояний. Условия, налагаемые на волновую функцию. Нормировка волновой функции.

Для некоторых практических задач потенциальная энергия частицы не зависит от времени. В этом случае волновую функцию 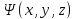можно представить как произведение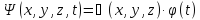

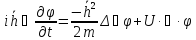т.к. 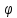зависит только от времени, то 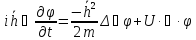разделим на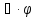получим:

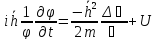
Левая часть равенства зависит только от времени, правая только от координат, это равенство справедливо только если обе части = const, такой константоя является полная энергия частицы Е.

Рассмотрим правую часть данного равенства: 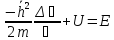, преобразуем:- уравнение для стационарного состояния.

Рассмотрим левую часть уравнения Шредингера: ;;

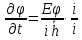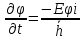разделим переменные 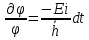, проинтегрируем полученное уравнение:

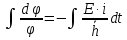воспользуясь математическими преобразованиями:

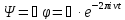
В этом случае вероятность нахождения частицы можно определить :

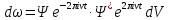, либо после преобразований:

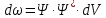–данная вероятность не зависит от времени, данное уравнение, характеризующее микрочастицы, получило название – стационарное состояние частицы.

Обычно требуют, чтобы волновая функция была определена и непрерывна (бесконечное число раз дифференцируема) во всем пространстве, а также чтобы она была однозначной. Допустимым является один вид неоднозначности волновых функций —неоднозначность знака «+/».

Волновая функция по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющему вид: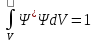

Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.

26 Частица в одномерной прямоугольной потенциальной яме бесконечной глубины. Квантование энергии. Принцип соответствия Бора.

Рассмотрим движение микрочастицы вдоль оси х в потенциальном поле.

Такое потенциальное поле соответствует бесконечно глубокой потенциальной яме с плоским дном. Примером движения в потенциальной яме является движение электрона в металле. Но для выхода электрона из металла необходимо совершить работу, что и соответствует потенциальной энергии в уравнении Шредингера.

При таком условии частица не проникает за пределы "ямы", т.е.

y(0)= y(l)=0 В пределах ямы (0<x<l) уравнение сведется к уравнению

илиданное уравнение является диференциальным уравнением и согласно математике его решение является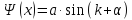, где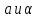можно определить из граничных условий.

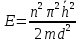n-главное квантовое число n=1,2,3…

Анализ этого уравнения показывает, что в потенциальной яме энергия не может быть дискретной величиной.

состояние с min энергией называется основным, все остальные возбужденные.

Рассмотрим 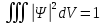т.к. потенциальная яма одномерна, то можно записать, чт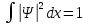о, в место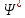подставим в выражение и получим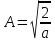. По скольку одномерная потенциальная яма с плоским дном, то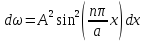

Графически изобразим

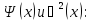
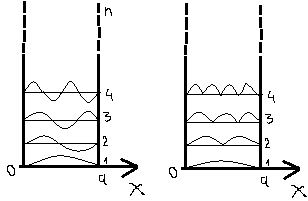
Из рисунка видно, что вероятность пребывания микрочастицы в разных местах отрезка неодинакова, с увеличением n вероятность нахождения частицы увеличивается

Квантование энергии является одним из ключевых принципов, необходимых для понимания структурной организации материи, т.е. существования стабильных, повторяющихся в своих свойствах, молекул, атомов и более мелких структурных единиц, из которых состоит как вещество, так и излучение.

Принцип квантования энергии гласит, что любая система взаимодействующих частиц, способная образовывать стабильное состояние — будь то кусок твердого тела, молекула, атом или атомное ядро, — может сделать это только при определенных значениях энергии.

В квантовой механике принципом соответствия называется утверждение о том, что поведение квантовомеханической системы стремится к классической физике в пределе больших квантовых чисел. Этот принцип ввёл Нильс Бор в 1923 году.

Правила квантовой механики очень успешно применяются в описании микроскопических объектов, типа атомов и элементарных частиц. С другой стороны, эксперименты показывают, что разнообразные макроскопические системы (пружина, конденсатор и т.д) можно достаточно точно описать в соответствии с классическими теориями, используя классическую механику и классическую электродинамику (хотя существуют макроскопические системы, демонстрирующие квантовое поведение, например, сверхтекучий жидкий гелий или сверхпроводники). Однако, весьма разумно полагать, что окончательные законы физики должны быть независимыми от размера описываемых физических объектов. Это предпосылка для принципа соответствия Бора, который утверждает, что классическая физика должна появиться как приближение к квантовой физике, поскольку системы становятся большими.

Условия, при которых квантовая и классическая механики совпадают, называются классическим пределом. Бор предложил грубый критерий для классического предела: переход происходит, когда квантовые числа, описывающие систему являются большими, означая или возбуждение системы до больших квантовых чисел, или то, что система описана большим набором квантовых чисел, или оба случая. Более современная формулировка говорит, что классическое приближение справедливо при больших значениях действия