
- •Методическое руководство по решению ситуационных задач контрольной работы студентов заочной формы обучения (приложение 1 )
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •1. Решение первой ситуационной задачи
- •2. Решение второй ситуационной задачи
- •3. Решение третьей ситуационной задачи
- •Построение начального опорного плана методом северо-западного угла
- •Нахождение оптимального плана методом потенциалов
- •4. Решение четвертой ситуационной задачи
- •4.2. Расчет временных характеристик сетевого графика и определение критических путей
- •4.3. Нахождение стратегии минимального удорожания для заданного сокращения срока строительства
3. Решение третьей ситуационной задачи
Примечание. Методическая разработка по решению транспортной задачи выполнена старшим преподавателем кафедры высшей математики Федоткиной Еленой Сергеевной.
Общее описание ситуации. Некоторый однородный продукт (груз) сосредоточен в m пунктах отправления (производства) в количествах а1, а2, …, am единиц соответственно. Его нужно доставить в n пунктов назначения (потребления), подавших заявки на этот продукт в количествах b1, b2, …, bn единиц соответственно. Предполагается, что сумма всех заявок равна сумме всех запасов, т.е. выполнено следующее условие:
![]() =
=![]() .
(3.1)
.
(3.1)
Это условие гарантирует, что все заявки будут выполнены полностью и из каждого пункта отправления будет вывезен весь груз.
Известны тарифы
(стоимости) cij
(![]() )
перевозки единицы груза из i‑го
пункта отправления в j-й
пункт назначения. Требуется найти план
перевозок, который удовлетворяет заявки
всех пунктов назначения и минимизирует
суммарные затраты на перевозку.
)
перевозки единицы груза из i‑го
пункта отправления в j-й
пункт назначения. Требуется найти план
перевозок, который удовлетворяет заявки
всех пунктов назначения и минимизирует
суммарные затраты на перевозку.
Математическая
модель. Для
построения модели описанной выше
ситуации, определим переменные xij
— количество груза, перевозимого из
i-го
пункта отправления в j-й
пункт назначения (![]() ).
Ясно, что они должны принимать
неотрицательные значения. Множество
всех переменных (план перевозок) задается
в виде матрицы X = (xij),
имеющей размеры mхn.
).
Ясно, что они должны принимать
неотрицательные значения. Множество
всех переменных (план перевозок) задается
в виде матрицы X = (xij),
имеющей размеры mхn.
Сама математическая модель задачи нахождения плана перевозок с наименьшими суммарными затратами выглядит так:
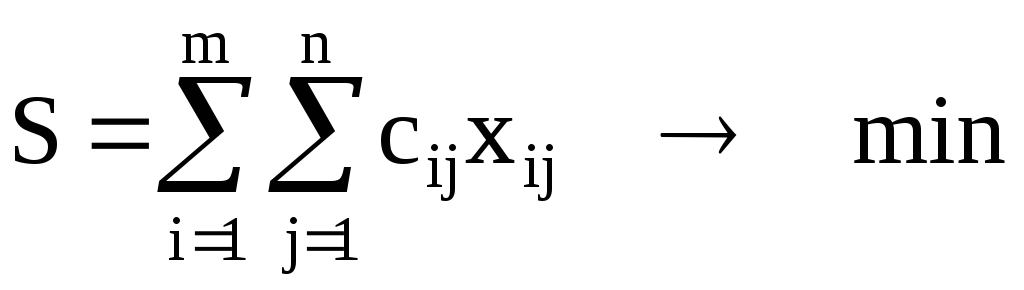 ,
(3.2)
,
(3.2)
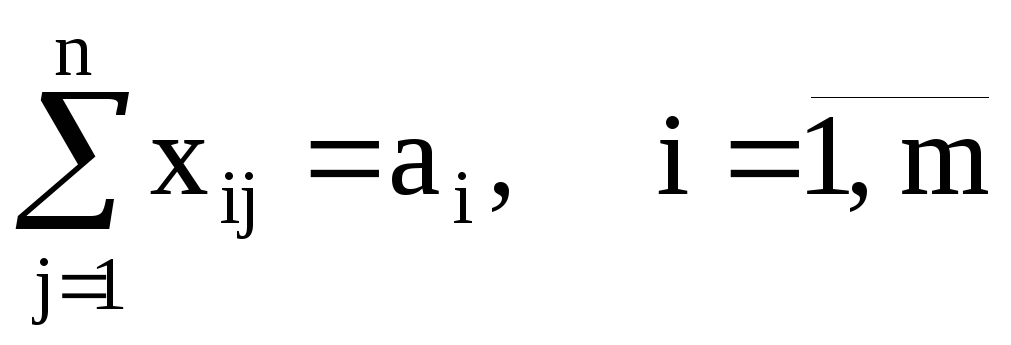 ,
(3.3)
,
(3.3)
 ,
(3.4)
,
(3.4)
![]() .
(3.5)
.
(3.5)
Формула (3.2) задает правило подсчета общих транспортных затрат S, необходимых для реализации плана перевозок X = (xij). Таким образом, S является целевой функцией, и решается задача ее минимизации на множестве планов перевозок, задаваемом ограничениями модели (3.3) – (3.5).
Условие (3.3) показывает, что общее количество груза, вывезенное из любого пункта отправления должно равняться величине запаса этого пункта. Условие (3.4) показывает, что общее количество груза, доставленное в любой пункт назначения должно равняться потребности этого пункта.
Задача (3.2) – (3.5) называется транспортной задачей, а равенства (3.3) – (3.4) называются условиями сбалансированности плана перевозок X = (xij).
План перевозок
X = (xij)
(![]() ),
удовлетворяющий соотношениям
(3.3) – (3.5),
называется допустимым
планом задачи
(3.2) – (3.5).
),
удовлетворяющий соотношениям
(3.3) – (3.5),
называется допустимым
планом задачи
(3.2) – (3.5).
Допустимый план
X* = (![]() )
называется оптимальным
планом,
если на
нем общая величина затрат на перевозки
S(X*)
минимальна.
)
называется оптимальным
планом,
если на
нем общая величина затрат на перевозки
S(X*)
минимальна.
Транспортная задача называется закрытой (сбалансированной), если выполнено условие (3.1). Это условие обеспечивает существование оптимального решения задачи (3.2) – (3.5).
Теорема 1. Транспортная задача имеет оптимальный план тогда и только тогда, когда она является закрытой.
Если условие (3.1) не выполнено, то транспортная задача называется открытой. В этом случае ее можно свести к закрытой задаче путем введения фиктивного пункта отправления или назначения (см. решение задачи 1).
Допустимый план транспортной задачи называется опорным планом, если столбцы матрицы условий, соответствующие его положительным компонентам, линейно независимы. Известно, что максимальное число линейно независимых столбцов матрицы условий транспортной задачи равно m + n – 1. Поэтому опорный план не может иметь более m + n – 1 положительных компонент. Если опорный план имеет ровно m + n – 1 положительных компонент, то он называется невырожденным планом, а если меньше, то вырожденным.
Транспортная задача является задачей линейного программирования, но она имеет ряд особенностей, отличающих ее от других задач этого типа:
все ее общие ограничения задаются в виде равенств;
все коэффициенты при переменных в ограничениях равны 1;
каждая переменная входит только в два ограничения.
Поэтому для решения транспортной задачи используются методы, учитывающие ее специфику. Стандартный метод ее решения включает следующие пункты:
1. построение начального опорного плана перевозок;
2. проверка полученного плана на оптимальность. Если он не является оптимальным, то строится новый улучшенный план перевозок, на котором транспортные затраты меньше, или, по крайней мере, равны затратам предыдущего плана. Этот пункт повторяется до тех пор, пока не будет получено оптимальное решение.
Нахождение начального опорного плана может осуществляться различными способами. Наиболее простыми в использовании являются метод северо-западного угла и метод минимального элемента.
При проверке на оптимальность допустимого плана используется следующий критерий.
Теорема 2.
Допустимый
план перевозок X* = (![]() )
в транспортной задаче будет оптимальным
тогда и только тогда, когда найдутся
числа u1,…,
um
и v1,
…,vn
такие, что выполнены следующие соотношения:
)
в транспортной задаче будет оптимальным
тогда и только тогда, когда найдутся
числа u1,…,
um
и v1,
…,vn
такие, что выполнены следующие соотношения:
vj – ui ≤ сij для всех i, j (3.6)
vj
– ui
= сij,
если
![]() >
0. (3.7)
>
0. (3.7)
Числа ui называются потенциалами пунктов отправления, а vj — потенциалами пунктов назначения. Условия (3.6) и (3.7) означают, что разность потенциалов между двумя любыми пунктами отправления и назначения в оптимальном плане не должна превосходить затрат на перевозку единицы груза. Если же между пунктами осуществляется перевозка, то разность потенциалов между ними в точности равна затратам на перевозку единицы груза. Потенциалы могут интерпретироваться как цены продукции в этих пунктах.
С помощью этого критерия можно не только проверить на оптимальность любой план перевозок, но и указать способ улучшения неоптимального плана. Для этого обычно используется метод потенциалов, который представляет собой модификацию симплекс-метода, учитывающую специфику транспортной задачи.
Решение предложенной
транспортной задачи должно начинаться
с проверки того, выполняется ли условие
ее закрытости, гарантирующее существование
оптимального плана перевозок. Для нашей
задачи это условие имеет вид:
![]() =
=![]() .
.
Вычислим
![]() =
118 + 18 + 98 = 234 и
=
118 + 18 + 98 = 234 и![]() =
68 + 68 + 90 + 31 + 87 = 344.
=
68 + 68 + 90 + 31 + 87 = 344.
Так как
![]() <
<![]() ,
то исходная транспортная задача не
является закрытой. Прежде чем приступить
к нахождению оптимального плана
перевозок, нужно сделать ее закрытой.
Для этого следует выполнить такие
действия:
,
то исходная транспортная задача не
является закрытой. Прежде чем приступить
к нахождению оптимального плана
перевозок, нужно сделать ее закрытой.
Для этого следует выполнить такие
действия:
Ввести четвертого (фиктивного) поставщика с объемом предложения а4 = 344 – 234 = 110 единиц;
Положить транспортные тарифы на перевозку грузов от этого поставщика ко всем потребителям равными нулю, т. е. с4j = 0, j =
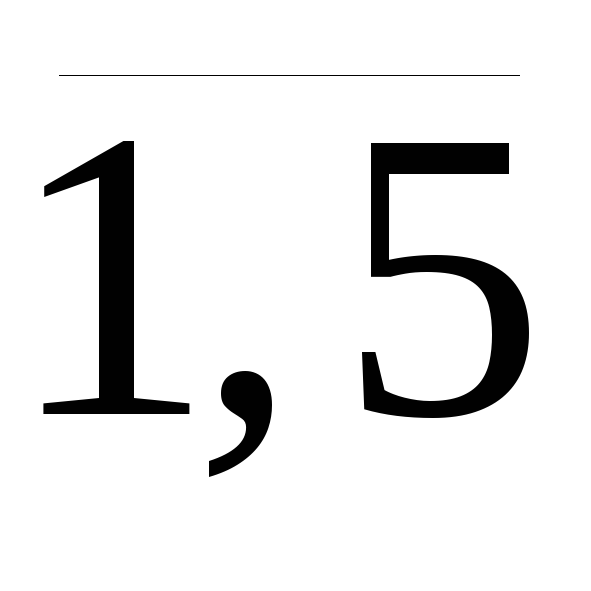 .
.
Замечание.Если окажется, что![]() >
>![]() ,
то в исходной задаче следует ввести
шестого (фиктивного) потребителя с
заявкойb6 =
,
то в исходной задаче следует ввести
шестого (фиктивного) потребителя с
заявкойb6 =![]() –
–![]() и положить тарифы на перевозку грузов
от всех поставщиков к этому потребителю
равными нулю, т. е. сi6 = 0,i=
и положить тарифы на перевозку грузов
от всех поставщиков к этому потребителю
равными нулю, т. е. сi6 = 0,i=![]() .
.
После добавления
фиктивного поставщика получена закрытая
транспортная задача, в которой число
поставщиков m
= 4, а число потребителей n
= 5. Обозначим хij
– объем поставки от i-го
поставщика к j-му
потребителю (i
=
![]() ,j =
,j =
![]() ).
Тогда модель новой транспортной задачи
имеет вид:
).
Тогда модель новой транспортной задачи
имеет вид:
x11 + x12 + x13 + x14 + x15 = 118, (3.8)
x21 + x22 + x23 + x24 + x25 = 18, (3.9)
x31 + x32 + x33 + x34 + x35 = 98, (3.10)
x41 + x42 + x43 + x44 + x45 = 110, (3.11)
x11 + x21 + x31 + x41 = 68 (3.12)
x12 + x22 + x32 + x42 = 68 (3.13)
x13 + x23 + x33 + x43 = 90 (3.14)
x14 + x24 + x34 + x44 = 31 (3.15)
x15 + x25 + x35 + x45 = 87 (3.16)
хij
![]() 0,
i
=
0,
i
= ![]() ,
j =
,
j =![]() .
(3.17)
.
(3.17)
S = 15x11 + 16x12 + 14x13 + 11x14 + 17x15 + 15x21 + 16x22 + 13x23 + 11x24 +
+ 14x25 + 21x31 + 22x32 + 16x33 + 16x34 + 23x35 → min. (3.18)
Для нахождения оптимального плана этой задачи ее следует представить в виде транспортной таблицы (см. табл. 3.1), строки которой соответствуют поставщикам, а столбцы – потребителям.
Таблица 3.1
|
bj ai |
68 |
68 |
90 |
31 |
87 |
|
118 |
15 x11 |
16 x12 |
14 x13 |
11 x14 |
17 x15 |
|
18 |
15 x21 |
16 x22 |
13 x23 |
11 x24 |
14 x25 |
|
98 |
21 х31 |
22 х32 |
16 x33 |
16 х34 |
23 x35 |
|
110 |
0 х41 |
0 х42 |
0 х43 |
0 х44 |
0 х45 |
В левом верхнем углу каждой клетки (i, j) помещается тариф данной перевозки cij, а сама клетка предназначается для размещения величины поставки xij из i-го пункта назначения в j-й пункт потребления. В клетки этой таблицы следует занести объемы перевозок, соответствующие начальному опорному плану. Этот план перевозок должен быть допустимым, т.е. составлен таким образом, чтобы выполнялись балансовые условия: общая сумма всех поставок от каждого поставщика (сумма по строке) равна объему его производства, а общая сумма поставок каждому потребителю (сумма по столбцу) — его спросу.
Клетки, в которые помещены какие-то перевозки, считаются занятыми, а остальные клетки — свободными. Занятые клетки транспортной таблицы соответствуют базисным, а свободные — небазисным компонентам опорного плана. Поскольку этот план должен быть опорным, то число занятых клеток в нем должно равняться m + n – 1 = 8. Проще всего построить такой план методом северо-западного угла.
