Конспект лекций по алгебре (семестр 2)

АЛГЕБРА

КОНСПЕКТ ЛЕКЦИЙ

СЕМЕСТР II

§1. Бинарные операции

Определение 1. Пусть M — произвольное множество. Говорят, что на множестве M задана бинарная операция, если указано правило, по которому каждой упорядоченной паре элементов из M сопоставляется элемент того же множества M .

Другими словами, бинарной операцией на M называется отображение

: M ×M →M .

Если на множестве M задана бинарная операция, то говорят также, что множество M замкнуто относительно этой операции.

На множестве M может быть задано, вообще говоря, много бинарных операций. Желая выделить одну из них, пишут (M , ) и говорят, что операция определяет на M алгебраическую структуру. Хорошо известными и важными примерами алгебраических структур являются следующие числовые множества

соперациями сложения и умножения:

— множество натуральных чисел;— множество целых чисел;

+= {0 } — множество неотрицательных целых чисел;

— множество рациональных чисел;— множество действительных чисел;

+ — множество неотрицательных действительных чисел.

Заметим, что операции сложения и умножения определены далеко не на всяком числовом множестве. Например, во множестве отрицательных целых чисел не определена операция умножения, так как произведение двух отрицательных чисел является положительным числом. Во множестве иррациональных чисел не определены ни сложение, ни умножение.

Рассмотрим примеры алгебраических структур, состоящих не из чисел. Пример 1. Операция композиции перестановок n элементов определяет на

множестве Sn алгебраическую структуру.

Пример 2. Множество арифметических векторов пространства m с операцией сложения векторов является алгебраической структурой.

Пример 3. На множестве всех матриц типа m×n операция сложения определяет алгебраическую структуру, а операция умножения нет.

Пример 4. Множество квадратных матриц порядка n образуют алгебраическую структуру относительно умножения матриц.

Нетрудно привести примеры числовых алгебраических структур с операция-

ми, отличных от сложения и умножения.
Пример 5.	( , ),	где операция		определена формулой	m n=−m−n.
Пример 6.	( , ),	где операция		определена формулой	m n=m+n+mn.
Пример 7.	( + , ),	где	m n — количество общих цифр в десятичной запи-
си чисел m и	n . Скажем,		1325 14536=3, а 14 52=0 .

В общем случае алгебраические структуры, как это демонстрируют послед-

ние примеры, могут быть довольно необычными. И их ценность на данном этапе развития математики не очевидна. По этой причине систематически изучаются в основном те алгебраические структуры, в которых бинарные операции подчиняются тем или иным ограничениям.

Определение 2. Бинарная операция	на множестве M называется ассоци-
ативной, если для любых a , b, c M	справедливо равенство

(a b)c=a (b c).

Определение 3. Бинарная операция на множестве M называется коммутативной, если для любых a , b M справедливо равенство

			a b=b a .
Всякое множество		M с заданной на нём ассоциативной бинарной операци-
ей	называется полугруппой.
Определение 4. Элемент			e M называется единичным относительно опера-
ции	, если для всех	a M	справедливо равенство

a e=e a=a .

Пример 8. В структуре (,) роль единичного элемента играет число 1. Пример 9. Единичная перестановка является единичным элементом в Sn .

Пример 10. Нулевой вектор 0 m является единичным элементом арифме-

тического векторного пространства m относительно сложения векторов. Пример 11. Множество не содержит единичного элемента относительно

операции , определенной формулой m n=−m−n.

Последний пример показывает, что единичного элемента в данной алгебраической структуре может и не существовать. Однако, как легко видеть, если единичный элемент существует, то он единственный. В самом деле, пусть e1

и e2 являются единичными элементами относительно . Тогда, согласно определению 4,

e1=e1 e2=e2 .

Полугруппу, содержащую единичный элемент, называют полугруппой с единицей или моноидом.

Определение 5. Пусть (M ,) — моноид. Элемент a M называется обратимым относительно операции , если найдётся такой элемент b M , что выполняется равенство

a b=b a=e .

Элемент b из последнего определения называется элементом, обратным к

элементу a и обозначается символом a−1 .

Произвольный элемент a моноида (M , ) может и не иметь обратного. Но если обратный элемент существует, то он единственный. В самом деле, если b1 и b2 — обратные к a , то

b1=b1 e=b1 (a b2)=(b1 a) b2=e b2=b2 .

Нетрудно видеть, что если элемент a обратимый, то обратимым является и элемент a−1 , причём обратный к нему совпадает с a , т. е. (a−1)−1=a .

Пример 12. Множество всех невырожденных матриц фиксированного порядка образуют моноид.

Замечание. В определениях 4 и 5 использовалась так называемая мультипликативная терминология, согласно которой бинарная операция называется умножением. В случае, когда операция коммутативна, бывает удобно использовать аддитивную терминологию. В этой терминологии бинарная операция называется сложением, единичный элемент — нулевым, а обратный элемент — противоположным.

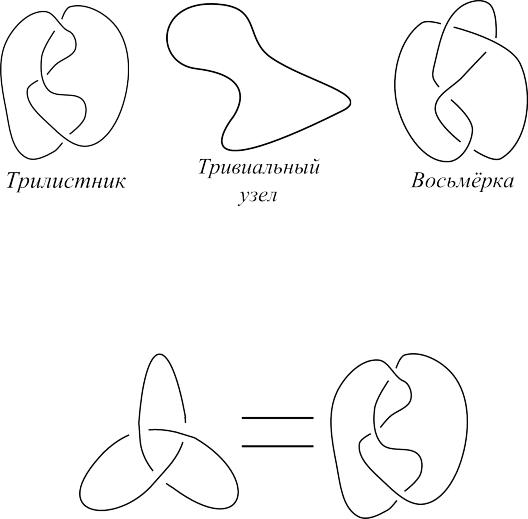
Пример 13. Возьмите верёвку, запутайте её любым способом и склейте концы. То, что получилось, называется узлом. Верёвку можно и не запутывать, а

сразу склеить её концы. Полученный узел называется тривиальным. Предположим, что материал, из которого сделана верёвка, эластичен настолько, что длина этой верёвки может быть сделана сколь угодно большой.

Рассмотрим множество всех узлов, которые можно получить из данного куска верёвки. Естественно, что два узла, полученные один из другого непрерывной деформацией верёвки, считаются одинаковыми.

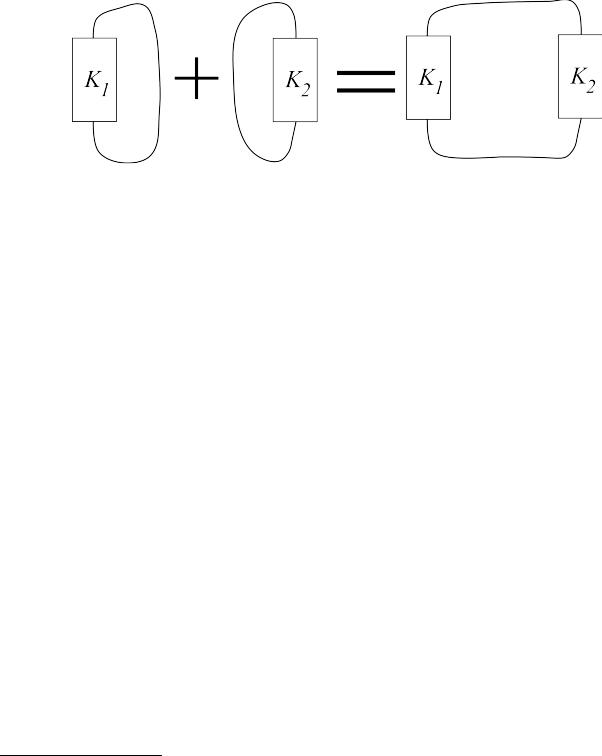
На этом множестве можно задать бинарную операцию, которую топологи1 называют связной суммой. Чтобы сложить два узла K 1 и K 2 , выберем на

каждом из них по незаузленному участку, вырежем эти участки и склеим освободившиеся концы.

Читателю предлагается показать, что определённая таким образом операция сложения задаёт на множестве всех узлов структуру коммутативного (!) моноида. Какой узел играет роль нулевого элемента в этом моноиде?

§2. Группы

В математике, её приложениях и смежных дисциплинах (химии, кристаллографии, теоретической физике) важную роль играют те моноиды, в которых каждый элемент является обратимым. Такие моноиды называются группами. Приведём подробное

Определение. Множество G относительно заданной на нём бинарной операции называется группой, если элементы G удовлетворяют следующим аксиомам:

1.	a , b ,c G (a b)c=a (b c);
2.	e G | a G a e=e a=a ;
3.	a G a−1 G | a a−1=a−1 a=e.

Если бинарная операция коммутативна (в определении группы этого свойства не требуется), то группа G называется коммутативной, или абелевой, по имени норвежского математика Н. Абеляi.

В случае, когда бинарная операция называется сложением, мы, как и выше, будем использовать аддитивную терминологию.

Пример 1. Структура (, +) является абелевой группой.

Пример 2. Структура (,) группой не является, поскольку в моноиде целых чисел есть только два обратимых элемента, 1 и −1.

Пример 3. Множество n арифметических n-векторов является абелевой

1Топология — это раздел математики, в котором изучают те свойства геометрических объектов, которые сохраняются при непрерывных деформациях этих объектов. Например, размерность, связность какой-нибудь фигуры, количество дыр в ней являются топологическими характеристиками этой фигуры. Напротив, форма и размеры фигуры не являются топологическими характеристиками. По этой причине топологи не могут различить сферу и поверхность куба.

группой относительно сложения.

Пример 4. Множество преобразований плоскости является группой относительно композиции. Эта группа не является абелевой.

Пример 5. Множество Sn перестановок n-элементного множества является группой относительно умножения. При n 3 группа Sn не является абелевой.

Примеры 4 и 5 можно обобщить следующим образом. Пусть X — произвольное множество. Совокупность всех преобразований этого множества обозначим через S ( X ). Другими словами, элементами S ( X ) являются все возможные биекции множества X на себя. Нетрудно показать, что S ( X ) является группой относительно композиции. Ассоциативность композиции и биективность id X тождественного отображения X на себя означают, что вы-

полняются аксиомы 1 и 2 из определения группы. Известно также, что отображение f −1 , обратное к биекции f , само является биекцией, причём имеют место соотношения f f −1= f −1 f =id X . Следовательно аксиома 3 также вы-

полняется.

Замечание. Исторически понятие группы возникло именно в связи с изучением преобразований тех или иных множеств. Поэтому, чтобы подчеркнуть самостоятельность понятия группы (в смысле данного выше определения), иногда говорят об абстрактной группе.

Если алгебраическая структура (G , ) является конечной, т. е. множество G состоит конечного числа элементов, то бинарную операцию можно в принципе задать при помощи таблицы Кэлиii, которая фактически представляет

собой таблицу умножения.

Пример 6. Зафиксируем некоторое натуральное число, например, m=4 и рассмотрим множество 4 остатков от деления целых чисел на 4. Элементами

этого множества являются числа 0,1,2,3. Произведением остатков a , b 4

назовём остаток от деления числа a b на 4. Обозначим введённую операцию через . Таблица Кэли в рассматриваемом случае будет иметь следующий вид:

	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

По этой таблице можно установить некоторые свойства алгебраической структуры (4 ,). Например, множество 4 замкнуто относительно ,

так как в зелёной части таблицы расположены те же элементы, что и в бирюзовой. Далее, элементы 2-й зелёной строки и 2-го зелёного столбца совпадают с соответствующими элементами бирюзовой строки и бирюзового столбца. Это означает, что 1 является единичным элементом относительно операции .

Симметричность элементов зелёной части относительно диагонали эквивалентна коммутативности операции .

Ассоциативность операции можно установить прямым (но утомитель-

ным) перебором или заметив, что оба произведения,

(a b) c и

a (b c), яв-

ляются остатками от деления числа

a b c на 4. В результате мы приходим к вы-

воду, что ( 4 , )

является коммутативным моноидом.

опре-

Аналогичным образом, на 4

можно ввести операцию сложения +,

̂

делив сумму остатков a , b 4

как остаток от деления числа

a+b

на 4. Та-

блица Кэли для операции сложения

+ будет иметь следующий вид:

̂

+

0

1

2

3

̂

0

0

1

2

3

1

1

2

3

0

2

2

3

0

1

3

3

0

1

2

Точно такими рассуждениями, что и выше, можно установить, что

( 4

,+)

̂

является абелевой группой.

Естественно, что число 4 можно заменить произвольным целым числом

m .

Возникающие при этом мультипликативные коммутативные моноиды

m иг-

рают важную роль в криптографии (особенно, если m — простое число).

Задача 1. Пусть g1 , g2 — элементы некоторой группы

G .

Выразите эле-

мент (g1 g2)−1 через g−1

1 , g−2

1 .

Задача 2. Докажите, что если

для всякого

элемента

g G

g g=e , то

группа G коммутативная.

§3. Подгруппы. Циклические группы

Пусть (G , ) — произвольная группа, H — подмножество в

G .

Определение 1. Подмножество

H называется подгруппой группы

G ,

если

оно является группой относительно операции

.

G иногда

Тот факт, что

H является

подгруппой

группы

записывают в

виде неравенства

H <G .

Обозначим единичный

элемент

в G через

eG .

Ясно,

что

{eG }

и

G яв-

ляются подгруппами группы G . Эти подгруппы называют тривиальными. Подгруппа H , отличная от G , называется собственной подгруппой.

Согласно определению группы, всякий её элемент обратим. Элемент, обратный к a обозначим временно через a−G1 .

Задача 1. Докажите, что если	H <G ,	то	eH =eG .
Задача 2. Докажите, что если	H <G ,	то для всякого a H a−H1=aG−1 .

Приведённые выше задачи показывают, что единичный элемент группы является и единичным элементом всякой её подгруппы и что элемент, обратный к элементу подгруппы лежит в этой подгруппе. Поэтому далее в обозначениях единичного и обратного элементов индекс, указывающий на подгруппу, будет опускаться.

Пример 1. Алгебраические структуры ( , +) и ( , +) являются группами. Так как , то ( , +) является подгруппой группы ( , +).

Пример 2. Алгебраические структуры ( 4 ,+)̂ и ( , +) являются группами относительно различных операций, поэтому несмотря на то, что множество

4={0,1,2,3} , ( 4 ,+)̂ не является подгруппой группы ( , +).

Теорема 1. Множество H G является подгруппой группы G тогда и только тогда, когда выполняются условия:

1. a ,b H a b H ;

2. a H a−1 H . Доказательство.

Необходимость условий 1-2 вытекает из определения подгруппы. Проверим их достаточность. Ассоциативность операции на H следует из того, что H является подмножеством в G . Условие 2 означает, что каждый элемент из H имеет обратный элемент, принадлежащий тому же множеству H . Остаётся показать, что единичный элемент e H . Для этого рассмотрим произвольный

элемент a H . По условию 2 a−1 H , а по условию 1 e=a a−1 H . □ Задача 3. Докажите, что подмножество H группы G является подгруппой

тогда и только тогда, когда a ,b H a b−1 H .

Пример 3. Алгебраическая структура ( , +) является группой. Зафиксиру-

ем целое число m и рассмотрим множество всех целых чисел, кратных			m .
Обозначим это множество символом	m .	Таким образом множество	m
состоит из всех чисел вида m a , где	a .	Равенства

m a+mb=m(a+b), −(ma)=m(−a)

означают, что (m , +) является подгруппой группы ( , +).

Пример 4. Рассмотрим множество G преобразований плоскости. Оно является группой относительно композиции. Пусть H — множество движений плоскости, т. е. преобразований, сохраняющих расстояние. Ясно, что если преобразование сохраняет расстояние на плоскости, то обратное ему также сохраняет расстояние. Аналогично, композиция сохраняющих расстояние преобразований также сохраняет расстояние. Теорема 1 позволяет утверждать, что H является подгруппой группы G . В частности, множество всех движений плоскости является группой относительно композиции.

Рассмотренный выше пример 3 можно обобщить следующим способом. Пусть (G , ) — мультипликативная группа и g — её фиксированный элемент. Введём следующие обозначения:

		g0=e, gn=g g … g , g−n=(g−1)n ,
		n множителей
где n	— натуральное число. Для всякого целого m элемент				gm называется
m -й	степенью g . Само число m называется показателем				gm .
Задача 4.		Докажите, что для любого	n	(gn )−1=(g−1 )n .
Задача 5.		Докажите, что для любых	m , n	gm gn=gm+ n .
Задача 6.		Докажите, что для любых	m , n	(gm)n=gm n .

Результаты задач 4, 5 позволяют заключить, что множество всех степеней эле-

мента g	образуют подгруппу группы	G . Эта подгруппа обозначается симво-
лом g .	Таким образом группа g	состоит из степеней элемента g .

Аналогичную конструкцию можно провести и в случае аддитивной группы.

Подгруппа g	состоит из кратных2 элемента g :				0 g=0 , n g=g+ g+…+g ,
(−n) g=n(−g)	при натуральном		n .			n слагаемых
Определение 2. Группа		G называется циклической, если существует такой
элемент g G ,	что G= g . Элемент			g называется		образующим цикличе-
ской группы G .
Пример 5. Аддитивная группа			целых чисел является циклической. В ка-
честве её образующих можно взять			1 или −1 .
Пример 6. Нетрудно видеть, что			m = m = −m .			Равенства
Пример 7. Рассмотрим аддитивную группу ( 4 ,+).
					̂
		̂	̂ ̂	̂ ̂	̂
	1=1,1+ 1=2 ,1+ 1+ 1=3,1+ 1+1 +1=0
означают, что группа ( 4		,+) является		циклической		с образующим элемен-
		̂

том 1.

Последний пример показывает, что множество степеней (кратных) элемента группы может оказаться конечным.

Определение 3. Порядком элемента g группы G называется наименьшее

натуральное число n , для которого gn=e . Если такого числа не существует, то порядок g считают равным бесконечности.

Задача 7. Докажите, что порядки элементов g и g−1 совпадают.

Задача 8. Пусть порядок g	равен n . Докажите, что:
а) элементы e , g , g2 ,…, gn−1	попарно различны;

б) для любого целого m элемент am совпадает с одним из перечисленных элементов.

Задача 9. Пусть g — элемент бесконечного порядка. Докажите, что элементы …, g−2 , g−1, e , g , g2 ,… попарно различны.

Задача 10. Пусть порядок g равен n . Докажите, что gm=e тогда и только тогда, когда m делится на n .

2 Обратите внимание, что в равенстве 0 g=0 символ 0 в левой части обозначает целое число, а справа — нейтральный элемент группы.

Задача 11. Пусть g1	и	g2	— перестановочные элементы группы		G ,		т. е.
g1 g2=g2 g1 , а числа	n1	и	n2 — их порядки. Докажите, что если		n1	и	n2
взаимно простые, то порядок			g1 g2 равен n1 n2 .
Теорема 2. Всякая подгруппа циклической группы является циклической.
Доказательство.
Пусть G — циклическая группа с образующей g ,				т. е. G= g ,	и	H	—
подгруппа группы G .	Всякий элемент из H лежит			в G , а потому		имеет

вид gk . Если H ={e}, то теорема доказана. В противном случае существует

положительное (почему?) целое l , для которого gl H . Наименьшее из этих чисел обозначим через l0 .

Пусть gk произвольный элемент из H . Разделим k на l0 :

k =l0 q+r ,0 r<l0 .

Следовательно g

k

=g

l

0 q

r

=(g

l0

q

r

и

g

r

=g

k

l0 −q

. Поскольку g

k

, g

l0

H и

g

) g

( g

)

H есть подгруппа, то

gr H . Неравенство

r >0

противоречит минимально-

сти l0 , поэтому r=0.

Значит всякий элемент подгруппы

H может быть за-

писан в виде gk =( gl 0)q,

т. е. элемент

gl0 является образующим группы H .

Другими словами

H = gl0

— циклическая группа. □

Задача 12. Докажите, что циклическая группа, состоящая из простого числа элементов, не имеет нетривиальных подгрупп.

Задача 13. Пусть циклическая группа G состоит из n элементов и n делится на k . Докажите, что в G существует подгруппа, состоящая из k элементов.

Замечание. Количество элементов в конечной группе называется порядком этой группы. В общем случае порядок группы не совпадает с порядком её элементов.

Задача 14. Докажите, что порядок группы G совпадает с порядком её элемента g тогда и только тогда, когда G является циклической с образующим элементом g .

§4. Гомоморфизмы и изоморфизмы групп

Рассмотрим две произвольные группы (G , ) и (F , ).

Определение 1. Отображение ϕ :G→ F называется гомоморфизмом, если для всех g1 , g2 G выполняется равенство ϕ(g1 g2)=ϕ( g1) ϕ( g2).

Говорят также, что гомоморфизм сохраняет групповую операцию, подразумевая под этим, что образ композиции элементов группы G равен композиции их образов в группе F :

ϕ

g1 g2→ϕ(g1) ϕ( g2).