16

Министерство образования Российской Федерации

Санкт - Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Лабораторная работа

По дисциплине	Вычислительные машины, системы и сети.

Методические указания

Тема:

Булева алгебра и комбинационные схемы

Составил

доцент

Фирсов А.Ю.

Санкт-Петербург

2003Год

Лабораторная работа 1

МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1

Булева алгебра и комбинационные схемы 1

Цель работы 3

Необходимые теоретически сведения. 3

Аксиомы и тождества Булевой алгебры. 3

Построение канонических выражений по таблице истинности. 8

Способы упрощения булевых выражений. 9

Построение логических диаграмм базисе И-НЕ (NAND-отрицание конъюнкции) 12

Построение логических диаграмм базисе ИЛИ-НЕ (NOR-отрицание дизъюнкции). 14

Построение временных диаграмм. 15

Порядок выполнения работы. 15

Цель работы

Цель работы – научиться применять теоретические основы Булевой алгебры для реализация булевых функций от нескольких переменных .

Необходимые теоретически сведения.

Все устройства ЭВМ состоят из элементарных логических элементов. Работа этих систем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания. В соответствии с такой двоичной природой высказывания условились называть его двоичной логической переменной X, которая принимает значение 1 в случае истинности и 0 в случае ложности. 1.

Аксиомы и тождества Булевой алгебры.

идемпотентные законы

коммутативные законы

ассоциативные законы

дистрибутивные законы

законы отрицания

законы двойственности (теоремы де Моргана)

закон двойного отрицания

законы поглощения (абсорбция)

операции склеивания

операции обобщенного склеивания

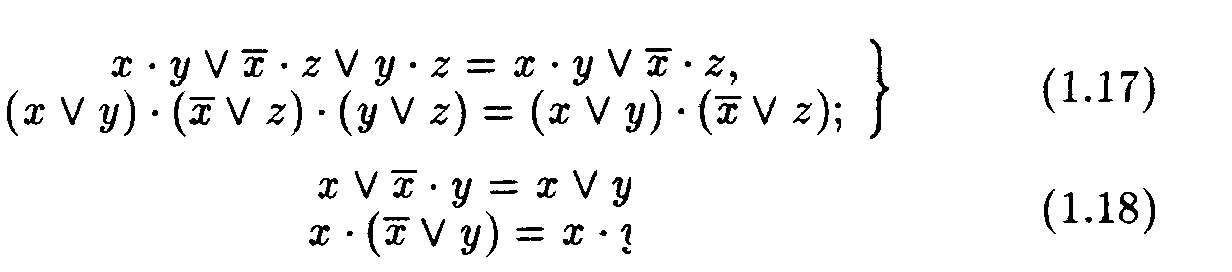
Теоремы (1.6) - (1.13) и (1.15) - (1.18) записаны парами, причем каждая из теорем пары двойственна другой, так как из одной теоремы пары можно получить другую на основании принципа двойственности, т.е. путем взаимной замены опера­ций дизъюнкции и конъюнкции, а также элементов 0 и 1, если они имеются. Теорема (1.14) самодвойственна, так как она не изменяется по принципу двойственности (отсутствуют элемен­ты 0 и 1 и операции дизъюнкции и конъюнкции). Все теоремы могут быть доказаны аналитически или методом перебора. В табл. 1.1 приведено доказательство одного из тождеств (1.13) методом перебора.

Таблица 1.1. Пример использования метода перебора

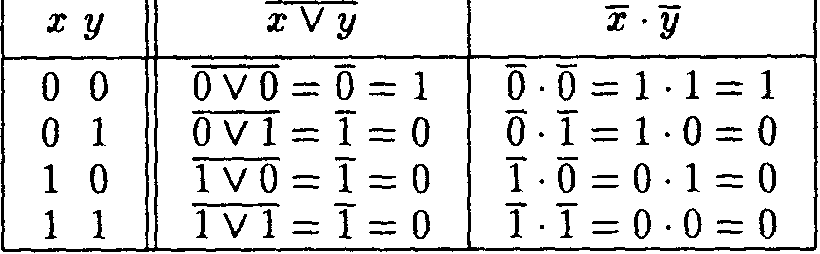
Такая таблица, в которой для всех возможных сочетаний входных переменных заданы значения Булевого выражения (Булевой функции) называется таблицей истинности, так как если две функции имеют одинаковую таблицу истинности, то они равны между собой.

Поскольку Булева алгебра является частным случаем теории множеств для случая, когда элементами множеств могут быть только логические нули и единицы, то для доказательства теорем БА можно применить графический метод теории множеств - круги Эйлера (рис.1.1).

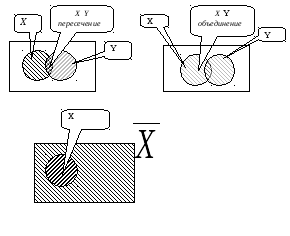
Рис. 1.1 Графический метод теории множеств - круги Эйлера .

Если в логическое выражение входят операции дизъюнкции и конъюнкции, то следует соблюдать порядок выполнения операций'. сначала выполняется операция конъюнкции, а затем — операция дизъюнкции. Этим устанавливается иерархия операций: конъюнкция — старшая операция, дизъюнкция — младшая. В сложных логиче­ских выражениях для задания порядка выполнения операций исполь­зуются скобки. Для упрощения записи выражений принято опускать те скобки, которые являются только подтверждением иерархии операций, например:.

Но скобки нельзя опустить в выражении .

Некоторые теоремы и тождества алгебры логики имеют особое значение, так как позволяют упрощать логические выражения. На­пример, в соотношениях (1.6), (1.10) - (1.12) и (1.15) - (1.18) пра­вая часть проще левой, поэтому, произведя в логических выражени­ях соответствующие преобразования, можно добиться существенного их упрощения. С этой целью особенно часто используются тождества (1.15)-(1.18).

Из каждой теоремы можно получить её разновидность, если одну из переменных заменить на её инверсное значение всюду в тождестве, описывающем суть теоремы. Например, полезной является разновидность теоремы поглощения . Теоремы можно также применять, если в качестве одной из переменных рассматривать целое выражение.

Для N входов таблица истинности содержит 2N строчек.

Если в таблицах для двух функций хотя бы одна строчка отличается, то эти функции различны. Поэтому общее число возможных различных функций от N переменных вычисляется по формуле

Следовательно, существует только 16 возможных функций двух переменных:

Таблица 1.2.

№	X 0	0	1	1	Обозна-чение	Название
	Y 0	1	0	1
0	0	0	0	0	0	Константа 0
1	0	0	0	1		Конъюнкция (логическое И)
2	0	0	1	0		Запрет по Y (отрицание импликации)
3	0	0	1	1	x	Повторение X
4	0	1	0	0		Запрет по X (отрицание импликации)
5	0	1	0	1	y	Повторение Y
6	0	1	1	0		Сумма по модулю 2 (исключающее ИЛИ)
7	0	1	1	1		Дизъюнкция (логическое ИЛИ)
8	1	0	0	0		Стрелка Пирса (отрицание дизъюнкции)
9	1	0	0	1		Эквивалентность
10	1	0	1	0		Отрицание Y (НЕ Y)
11	1	0	1	1		Импликация от Y к X
12	1	1	0	0		Отрицание X (НЕ X)
13	1	1	0	1		Импликация от X к Y
14	1	1	1	0		Штрих Шеффера (отрикание конъюнкции)
15	1	1	1	1	1	Константа 1

Из 16 возможных функций двух переменных наибольший практический интерес представляют основные функции (отрицания, конъюнкции и дизъюнкции) и универсальные функции (отрицание конъюнкции и отрицание дизъюнкции), так как другие функции можно выразить через них.

Операции дизъюнкции, конъюнкции и отрицания легко реализо­вать довольно простыми контактными (релейными) цепями и элек­тронными схемами с односторонней проводимостью, имеющими ко­нечное число входов и один выход и называемыми логическими эле­ментами (ЛЭ).

Основные логические элементы Logic Works соответствуют основным операциям Булевой алгебры (табл.1.3)

Таблица 1.3

Название	Обозначение в Logic Works	Название элемента в Logic Works
Конъюнкция (логическое И)		AND-2
Дизъюнкция (логическое ИЛИ)		OR-2
Отрицание (НЕ)		NOT

Табл.1.4. Обозначения основных операций Булевой алгебры в различных областях применения.
Название	конъюнкция логическое И	дизъюнк­ция логическое ИЛИ	отрицание, инверсия логическое НЕ	сложение по модулю 2 исключающее ИЛИ
Область применения обозначений
Булева алгебра	x • y	x + y		x y
Булева алгебра	x y	x y		x y
Булева алгебра	x y	x y		x Ф y
Логика	x & y	x V y	┐x
Теория множеств	x y пересечение	x y объединение	дополнение до 1
Языки программирования	x AND y	x OR y	NOT x	x XOR y
Язык Си (логические)	x && y	x || y	!x
Язык Си (поразрядные)	x & y	x | y	-x (обратный код)	x - y

Как следует из сопоставления табл.1.3 и рис.1.2, в Logic Works принят стандарт США.

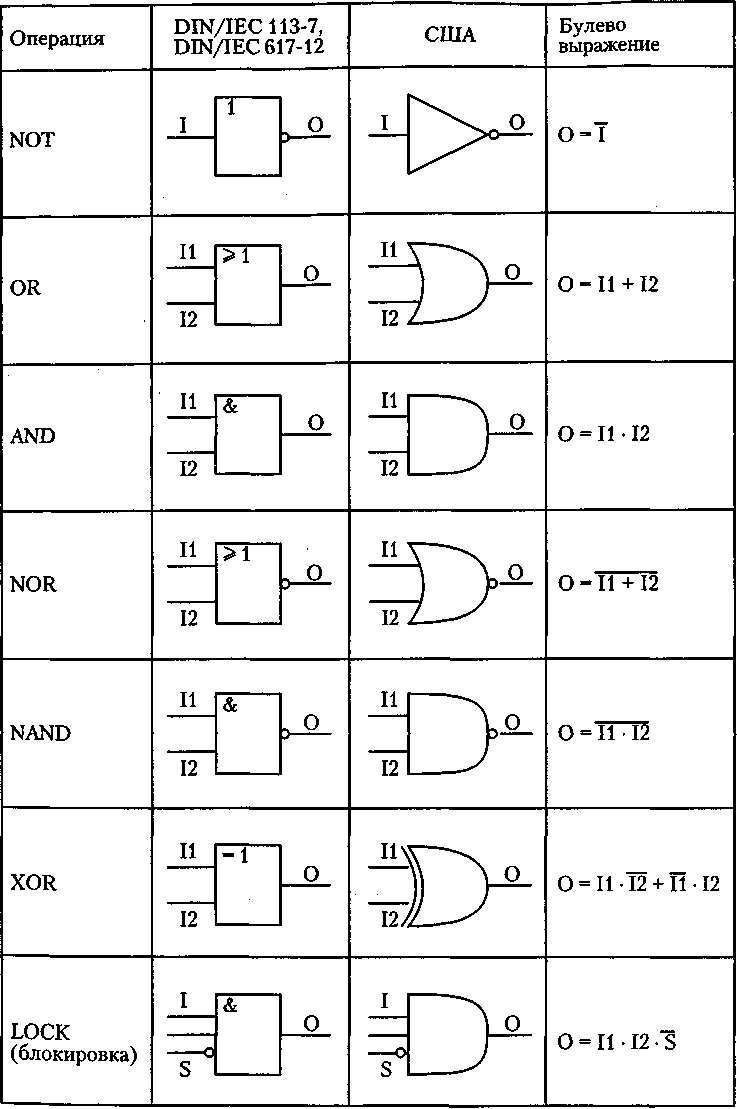
Рис.1.2.Стандарты обозначения логических элементов на схемах.