Практическое занятие 17 приём И.З

(7.1)

S x dx .

Лекция 7. Приложение определённого интеграла к задачам вычисления объёмов тел и длин дуг кривых линий.

z

a

x

b

S S(x)

y

xрис.1.

Пусть некоторый объём находится в координатном пространстве между плоскостями

x a и x b . Через произвольную точку x, лежащую на оси OX , x a;b проводим плоскость перпендикулярную оси OX . Эта плоскость рассекает объём , образуя сечение площадь которого обозначим через S x . Это сечение символически можно считать бесконечно тонким цилиндром толщины dx . Таким образом этот неделимый объём dV равен dV

Весь объём можно считать состоящим из таких неделимых объёмов. Отсюда

b

V S x dx

a

Пример 1. Найти объём прямого цилиндра высотой 7м, основанием которого является эллипс,

		x2		y2
задаваемый уравнением					1.
		4	9
Решение. На прошлом занятии мы доказали, что площадь эллипса						x2		y2	1даётся формулой
						a2		b2
S	ab .Направим ось симметрии цилиндра вдоль оси OZ . Произведём сечение цилиндра
плоскостью
z	t, причёмt 0; 4 . Сечением при любом t будет эллипс, площадью S t									ab .

Объём вычисляем по формуле (7.1)

b

4

V

S x dx

2 3dt 6 t

4

24 м3;

0

a

0

Пример 2. Найти объём кругового конуса,

ограниченного конической поверхностью

z

x2 y2

и плоскостью z

3 .

Решение. Произведём сечение конуса плоскостью

z t, причёмt

0;9

. Сечением будет круг,

уравнение которого x2

y2

t2 . Следовательно,

радиус круга R

t . Площадь сечения это

площадь круга S t

R2

t2 . Объём вычисляем по формуле (7.1)

b

3

t3

V

S x dx

t2dt

3

9 м3

3

0

a

0

Пример 3. Найти объём тела, ограниченного параболоидом z

x2

y2

и плоскостью z

5 .

Решение. Произведём сечение тела плоскостью z

t, причёмt

0;5 . Сечением будет круг,

уравнение которого x2

y2

t . Следовательно, радиус круга R

t . Площадь сечения это

площадь круга S

t

R2

t . Объём вычисляем по формуле (8.1)

b

5

t

2

V

S

x dx

tdt

5

12.5

м3

2

0

a

0

Вычисление объёмов тел вращения .Вращение вокруг оси

OX

На плоскости OXY рассмотрим криволинейную трапецию, ограниченную кривыми :

y

y1 x и y

y2

x и прямыми x

a, x

b .

y f x

у=g(x)

Y

y g x

y g x

	a	x	y g x
			b	X

y g x

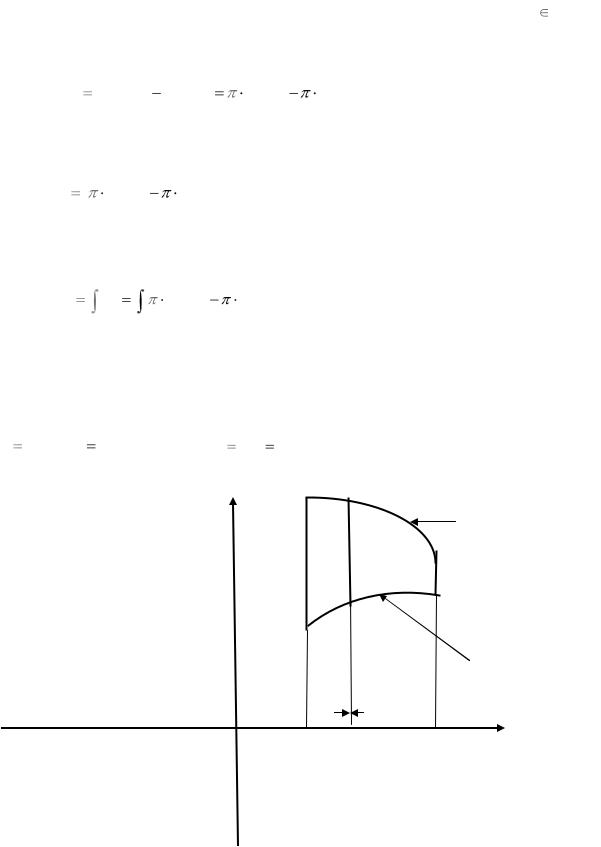
рис. 2

Как и в предыдущих задачах через произвольную точку x, лежащую на оси OX , x a;b

проводим плоскость перпендикулярную оси OX . Эта плоскость рассекает объём , образуя сечение площадь которого обозначим через S x :

S x S	MAX	x S x	y 2	x	y 2	x .
		min	1		2

Это сечение символически можно считать бесконечно тонким цилиндром толщины dx . Таким образом, этот элементарный неуменьшаемый по толщине объём dV равен

dV [ y 2	x	y 2	x ]dx .
1		2

Весь объём можно считать равным сумме этих элементарных объёмов т.е. определённому

интегралу.	Отсюда
	b	b
V	dV	[ y 2	x	y 2	x ]dx	(7.2)
		1		2
	a	a

Вращение вокруг оси OY

На плоскости OXY рассмотрим криволинейную трапецию ABCD, ограниченную кривыми : y y1 x и y y2 x и прямыми x a, x b .

A

Y

y1 x

B

C

D

	dx	y2 x
a	x	b

рис.3

Трапеция ABCD вращается вокруг оси OY . Вычислим объём полученного тела вращения. Для

произвольного x	a;b , вырежем в трапеции элементарную полоску шириной dx . Площадь
полоски равна dS	y1 x y2 x dx . Полоска, как и трапеция, вращаясь вокруг оси OX

образует тончайшее цилиндрическое кольцо. Можно считать это кольцо намотанным на цилиндр

радиуса x . Если длину этой цилиндрической ленты 2									x умножить на площадь её торца
dS	y1	x	y2	x	dx , то получим объём этого элементарного цилиндрического кольца
dV	2	x dS	2	x	y1 x	y2	x	dx см. рис.3 . Объём , полученный от вращения трапеции
вокруг оси OY , будет равен сумме объёмов этих элементарных колец то есть определённому
интегралу
				b
			V		2 x y1	x	y2	x dx	(7.3)

a

2 x

x

x

dS

рис.4

Рассмотрим примеры.

Пример 4. Вычислить объём тела, образованного вращением трапеции, ограниченной

	линиями: y	x3		вокруг: а) оси ОХ, б) оси ОУ.
			, y 0, x 0, x 3,
		9

Решение. При решении пункта а) применяем формулу (7.2). Для этого полагаем в

формуле (7.2)		x2				Отсюда объём тела вращения равен
	a 0, b 3, y x		, y	2	x 0;
	1	9

	b dV	b [	y 2		y 2		3	x3	2	3 x6				x7			3
V				x		x ]dx			dx				dx
																	0
	a	a	1		2		0	9		0 81				81 7

	27	12.11м 3 .
	7

Решаем пункт б). При решении пункта б) применяем формулу (7.3). Для этого полагаем

в формуле (15.3)		x2				Отсюда объём тела вращения равен
	a 0, b 3, y x		, y	2	x 0;
	1	9

b	3	x3		x5
V	2 y1 x y2 x dx = 2 x		2				3
		9		45			0
a	0

	54	34м3
	5

Пример 5. Вычислить объём тела, образованного вращением трапеции, ограниченной

линиями: y x2 , y x ,вокруг: а) оси ОХ, б) оси ОУ.

Решаем пункт а). Данные линии параболы. Они пересекаются в точках 0;0 и 1;1

см.рис.5.

При решении пункта а) применяем формулу (15.2). Для этого полагаем в формуле (7.2 )

					x2 , a		0,b 1. Отсюда объём тела
y		x, y
1	2
вращения равен
	1				2		2 dx
						x2
V				x
	0

x2		x5
				1
2	5			0

	1	1		3		0.9м3
	2	5		10

Рис.5.

При решении пункта б) применяем формулу (7.3). Для этого полагаем в формуле (7.3 )

y		x, y x2		, a	0,b 1. Отсюда объём тела вращения равен
1	2
b						1			1	3		5					4
												2	x			x
						x dx = 2 x x x2					x3 ]dx 2								1
V	2 x y x y								dx 2 [x2					2
					2														0
	1											5			4
a						0			0

	3	0.9
	10

Вычисление длин участков линий заданных различными уравнениями.

Правило 1. Пусть функция y

y x , x

a;b имеет непрерывную производную. Если кривая

линия задана на координатной плоскости явным образом т.е.

y

y x , x

a;b , то длина дуги

кривой L от точки A a; y a

до точки B b; y b

вычисляется по формуле

b

2 dx

(7.4)

L

1

y

x

a

Правило 2.

Пусть функции x

x t

, y

y

t ,

t

имеют непрерывные производные. Если

кривая линия задана параметрическими уравнениями,

т.е. x

x

t , y y

t ,

t

,то длина

дуги кривой L от точки A x

; y

до точки B x

; y

вычисляется по формуле

L

x

t

2

y

t

2 dt

(7.5)

Правило 3. Пусть функция

,

имеет непрерывную производную. Если кривая

линия задана уравнением в полярных координатах

т.е.

,

, то длина дуги

кривой L от точки A

;

до точки B

;

вычисляется по формуле

L

2

2 d

(7.6)

Докажем правило 1 . Пусть кривая задана уравнением

y y

x . Начальную и конечную точки

кривой обозначим соответственно через A a; y a

, B b; y b

. Разобьём отрезок a;b на

участки x0

a x1 x2 ...

xk 1

xk

...

xn

b

и приблизим кривую L ломаной линией P .

На рис.6.Изображен участок дуги кривой и соответствующее звено ломаной линии

Pk .

Ak xk ; y xk

,

Bk xk ; y xk

рис.6

Длина Pk , звена ломаной , вычисляется по теореме Пифагора

Pk

xk

xk 1

2

y xk

y xk 1

2

=

по теореме о среднем в дифференцировании

x

x

2

y c

2 (x

x

)2

k

k 1

k

k

k 1

1

y

ck

2

xk

Отсюда длина всей ломаной равна интегральной сумме

P

1

y

c1

2

x1

1

y c2

2

x2 ...

(7.7)

1

y

xk

2

xk

...

1

y

xn

2 xn

Так как функция

1

y

x

2

непрерывна, то по теореме 3.1 интегральная сумма (7.7)

b

имеет при

x

0 предельным значением определённый интеграл

2 dx

1

y x

a

Правила 2,3 доказываются аналогично. Примем их без доказательства.

Рассмотрим примеры.

x

x

Пример 6.

Вычислить длину цепной линии y

e2

e 2 , x

0; 2 .

x

x

Решение. Кривая задана явным уравнением y

e2

e 2 , x

0; 2 . Предварительно

x

x

x

x

2

x

x

вычисляем

y

e2

e 2

1

e2

e 2

e2

e 2

.

2

2

2

x

x

Применяем правило 1 формула (7.4). Для этого полагаем в формуле (7.4 ) y e2

e 2 , x 0; 2 ,

a

0, b 2; Отсюда

x

x

b

2 e

2

e

2

x

x

1

2

dx =

2

2.35 м .

L

1

y

x

dx

e2

e

2

e

2

0

e

a

0

Пример 7.

Найти длину арки циклоиды: x

1

sin t; y 1

cos t;

Решение. Применяем правило 2 формула (7.5). Для этого полагаем в формуле (7.5 )

x

1 sin t; y

1

cos t;

0;

2 .

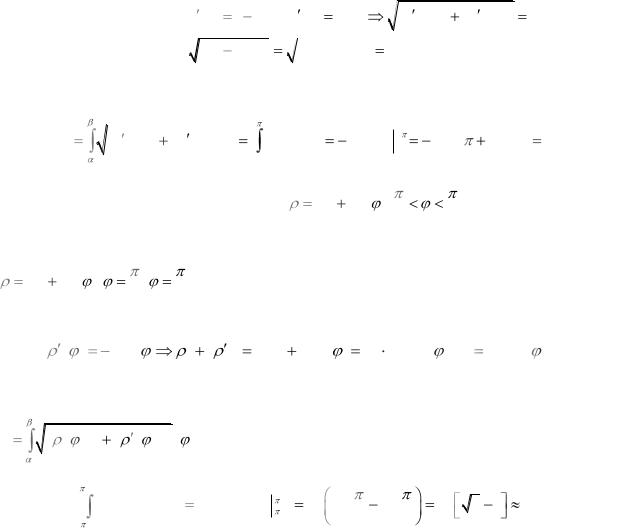
x t		1 cos t; y t			sin t;	x	t	2	y t	2
Предварительно вычисляем
2 1		cos t		4sin2	t / 2	2sin	t / 2

Подставляя данные в формулу (7.5), получаем

					2
L	x t	2	y t	2 dt

0

2sin	t	dt	4 cos	t
2			2

	2	4 cos	4 cos 0 8;
	0

Пример 8. Вычислить длину дуги кардиоиды	7(1 cos ),				;
		3		2

Решение. Применяем правило 3 формула (7.6). Для этого полагаем в формуле (7.6 )

7(1 cos ),		,		;
	3		2

Предварительно вычисляем

7sin ,

2 ( )2 49(2 2cos ) 49 4cos2 / 2 14cos / 2 .

Подставляя данные в формулу (7.6), получаем

L	2	2 d	=
	/2
7	2 cos t / 2	dt	28sin t / 2
	/3

/2
	28 sin		sin		14 2 1 5.7;
/3
	4			6

Контрольные вопросы.

I.Как найти объём тела, расположенного между параллельными плоскостями, если известны площади поперечных сечений, параллельных этим плоскостям.

II. Как найти объём тела, образованного вращением криволинейной трапеции

вокруг осей: 1) OX , 2) OY ?

III. Как выражается дифференциал длины дуги кривой в прямоугольных координатах? IV. Как выражается дифференциал длины дуги кривой заданной в параметрическом

виде?

V. Как выражается дифференциал длины дуги кривой в полярных координатах? VI. Приведите формулы вычисления длины дуги кривой , заданной различными

способами.

Практическое занятие 7. Вычисление объёмов тел. Вычисление длин дуг кривых.

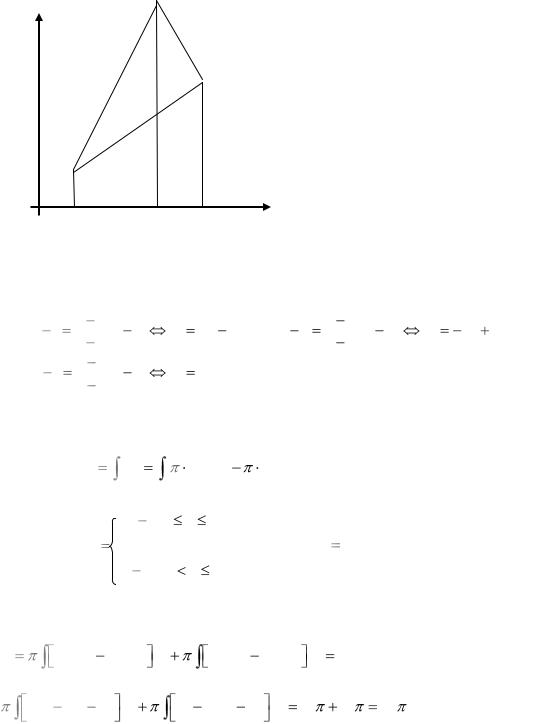
Чтобы правильно вычислять объёмы, полученные от вращения плоских областей, вокруг координатных осей рассмотрим два примера.

Пример 1. Вычислить объём, полученный отвращения вокруг оси ОХ треугольника АВС (рис.1)

В( 2;5 )

С(3;3)

D

А(1;1

рис.1

Решение. Найдём уравнения прямых линий ограничивающих данный треугольник.

		5		1					5	3
	AB : y 1				x 1	y 4x 3		; BC : y 3			x 3	y 2x 9
		2		1					2	3
			3	1
	AC : y 1				x 1	y x
		3		1

Для вычисления объёма вращения применяем формулу

			b			b
		V		dV		[	y 2	x	y 2	x ]dx	(7.2)
							1		2
			a			a
				4x		3, 1	x	2;
Функция	y1	x						, функция y2 x x .
				9	2x, 2 x 3
Отсюда
2							3
V	y2	x y		2	x dx			y2	x y2	x dx
	1		2					1	2
1							2
2						3
4x 3 2			x2 dx				9 2x 2		x2 dx 12 10		22
1						2

Пример 2. Вычислить объём, полученный отвращения вокруг оси ОУ треугольника АВС (рис.1)

Решение. Найдём уравнения прямых линий ограничивающих данный треугольник.

		5		1					5	3
	AB : y 1				x 1	y 4x 3		; BC : y 3			x 3	y 2x 9
		2		1					2	3
			3	1
	AC : y 1				x 1	y x
		3		1

Для вычисления объёма вращения применяем формулу

b
V	2 x	y1	x y2 x dx	(7.3)
a
4x	3, 1	x	2;
Функция y1 x			, функция y2 x	x .
9 2x, 2 x 3
Отсюда
2			3
V 2 x y1 x y2 x dx 2 x y1 x y2 x dx
1			2
2	3
2 x 4x 3 x dx 2 x 9 2x x dx 5 7				12
1	2

1. Вычислить объёмы тел, у которых известны площади сечений перпендикулярных заданной оси

	1)	S	x	x2 3x, x		1;5 , осьOX ;
	2)	S	y	y(2	3y),	y 0;3 , осьOY ;
Указание. Используйте формулу если S z , z					a;b площади поперечных сечений тела, то
	b
V	S z dz .

a

2. Вычислить объёмы тел, образованных вращением областей D, ограниченных линиями

1) y x2 , y 0, 0 x 1;	2) y sin x, y	0, x 0;	; 3) y			2x x2 , y 0, 0 x 2;
4) y ex , y e x , x 1;	5) y x2 , y2	x; 6) y	1		; y	1	;1 x 2;
				x		x
вокруг осей 1) OX , 2) OY ;
Решаем 1. Рисуем область	D

рис.1