УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА

Основное свойство уравнений гиперболического типа – наличие полного набора вещественных характеристик.

Характеристики: направления, вдоль которых уравнение можно проинтегрировать

Примеры уравнений гиперболического типа:

линейное уравнение переноса (адвекции)

u	C	u	0,	u u(x, t),	C const;
t		x

квазилинейное уравнение вида закона сохранения

u (u) 0;t x

волновое уравнение	2u	c2 2u	0,
	t2	x2

ЛИНЕЙНОЕ УРАВНЕНИЕ ПЕРЕНОСА

Характеристиками уравнения являются прямые dxdt C

t

t*

x

x x0*		x*

Запишем производную от решения по характеристическому направлению:

du(x(t), t) dt

dx C dt

	u dx		u		u C	u	0
	x dt		t		x	t

Вдоль данного направления решение уравнения не изменяется.

Поэтому говорят, что решение уравнения «переносится вдоль характеристик».

ЗАДАЧА КОШИ

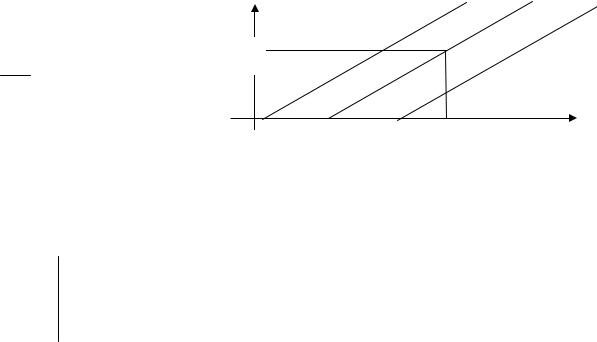
Заданы начальные данные u(x, 0) (x), нужно найти решение в точке (x* , t* ) . Построим поле характеристик и определим точку на прямой t 0 , в которую приходит «выпущенная» из точки (x* , t* ) характеристика: x x0* Решение сохраняется вдоль характеристик, поэтому u(x* , t* ) (x0* ) .

Если начальные данные заданы на характеристика, выпущенная из любой t > 0, пересечет линию t = 0. Поэтому времени определяется как u(x, t) (x Ct) .

всей прямой t = 0, то точки полуплоскости (x, t), решение в любой момент

НАЧАЛЬНО-КРАЕВАЯ ЗАДАЧА

Пусть начальные данные заданы в ограниченной области: 0 x L , и требуется определить решение при t T. Выпустим из каждой точки отрезка [0, L] характеристики. В зависимости от знака С они закроют правую или левую часть прямоугольника [0 t T ] [0 x L]

t = T	t =
	С > 0	С < 0
	x	x
	L	L

Для того, чтобы определить решение во всем прямоугольнике, необходимо задать краевые условия.

Если С > 0, краевые условия при x = 0, если С < 0 –при x = L. Корректная постановка условий для гиперболических уравнений:

На каждой границе области решения необходимо задать столько условий, сколько семейств характеристик уходит с этой границы.

ПРИБЛИЖЕННЫЕ МЕТОДЫ

Для аппроксимации производной по пространству используем формулы: разность вперед, разность назад или центральная разность Необходимо учитывать направление потока – знак константы С.

При С > 0 поток направлен слева направо, при С < 0 – справа налево. Пусть С > 0. Явная схема «против потока»:

	un 1		un			un un
		j	j	C		j	j 1	0.
							h
unj 1 unj		C unj			unj 1 (1 r)unj				runj 1 ,
			h

r = Сτ/h – число Куранта.

x*

tn+1

x*

t

n+ 1

x*

t

n+1

t

n

t

n

t

n

xj–1

xj

xj–1

xj

xj–1

xj

r<1

r=1

r>1

УСТОЙЧИВОСТЬ СХЕМЫ

Метод Фурье: гармоника unj n eij . Подставим в разностную схему:

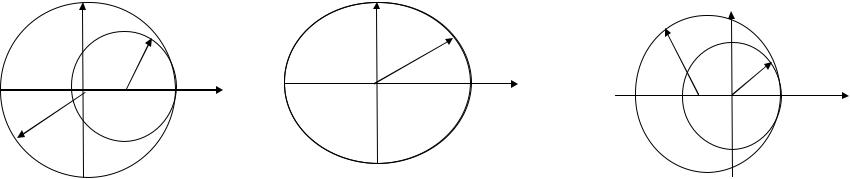
(1 r) re i (1 r) r(cos i sin ) .

Окружность радиуса r с центром в точке (1 – r, 0)

y

y

y

r

r = 1

r

1 – 2r

1

1

x

x

x

1 – r

1

1

1 – r

r < 1

r = 1

r > 1

При r 1 разностная схема устойчива При r > 1 - неустойчива

УСТОЙЧИВОСТЬ СХЕМЫ

Аналитические исследования

(1 r) re i (1 r) r(cos i sin )

1 r(1 cos ) ir sin 1 2r sin2 2 ir sin .

Оценим модуль комплексного числа ρ:

			2	1 4r sin2				4r2 sin4			r2 sin2
							2			2
1 4r sin					2		4r2 sin4		4r2 sin		2 cos2
						2		2			2	2
1 4r sin					2		4r2 sin2		1,	4r sin2		4r2 sin2	0,
4r sin2						2		2			2	2
					(1 r) 0,
2

что справедливо при r 1 (условие Куранта).

ЯВНАЯ СХЕМА ПО ПОТОКУ:

unj 1 unj

C

unj 1 unj

0

un 1

un

C un

un (1 r)un run

.

,

h

j

j

h

j 1

j

j

j 1

Метод Фурье (1 r) rei (1 r) r(cos i sin )

1 при любом r, следовательно схема абсолютно неустойчива

а	tn+1	б	y
		1
x*			r
	tn		1+ r
				x
xj	xj+1

	un 1 un		C	un	un
Явная схема с центральной разностью	j	j		j 1	j 1
					2h

0

второй порядок аппроксимации по пространству

абсолютно неустойчива

НЕЯВНЫЕ СХЕМЫ

un 1	un		un 1	un 1		un 1	un		un 1	un 1
j	j	C	j	j 1	0	j	j	C	j 1	j	0
				h						h
против потока (С>0)						по потоку (С>0)

первый порядок аппроксимации по времени и пространству

при C > 0 схема против потока абсолютно устойчива, схема по потоку условно устойчива при r 1

при C < 0 схема с «разностью вперед» абсолютно устойчива, схема с «разностью назад» условно устойчива при r 1

УРАВНЕНИЕ С ПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ

u	C(x,t)	u	0 , 0 x L ,	t 0
t		x

устойчивая аппроксимация зависит от знака С(x, t)

 гибридная схему Куранта – Изаксона – Риса (КИР):

unj 1 unj

C j

C j

unj

unj 1

C j

C j

unj 1

unj 1

0

2

h

2

h

 симметричная схема

un 1 un 1

un un

un 1 un (un 1

un

)

j

j 1

j j 1

C

j

j

j 1

j 1

0

 схема Лакса

2

2h

unj

1 unj

C j

unj 1 unj 1

h2

unj 1 2unj

unj 1

0

2h

2

h2

ДВУХШАГОВЫЕ СХЕМЫ

 схема Лакса – Вендрофа

un 1/ 2

un

un

un

j 1/ 2

j 1/ 2

C j

j

j 1

0

(предиктор),

h

n 1

n

n 1/ 2

n 1/ 2

u j

u j

C j

u j 1/ 2

u j 1/ 2

0

(корректор),

h

 схема Мак-Кормака

~

n

n

n

u j

u j

C j

u j 1

u j

0

(предиктор),

h

u

u

u

u

u

n 1

n

C u

n

n

~

~

j

j

j

j 1

j

j

j 1

0 (корректор).

2

h

h