2 семестр / ПОСОБИЕ_ВычМат

11

3.2. Если sgn f(x) = 0, то получено решение; выполнить выход из цикла.

Иначе	3.3. Если sgn f(x)= sgnf(a), то	принимаем a = x
	иначе принимаем b = x.
4.	Конец цикла.
5.	Вывод x – приближенного значения корня.
6.	Конец алгоритма.

1.2.4 Метод итераций
Заменим уравнение (1) равносильным уравнением
x = ϕ(x).	(8)

Если любая точка x0 интервала [a; b] изоляции корня есть приближение нуля функции f(x), то следующее приближение получается так:

x1 = ϕ(x0).

Подставляя теперь в правую часть последнего равенства вместо x0 число x1, получим новое число

x2 = ϕ(x1).

Повторяя этот процесс, будем иметь последовательность чисел

xn = ϕ(xn–1) n = 1, 2, …		(9)
Если эта последовательность сходящаяся, т.е.
	lim xn = ξ,	(10)
	n →∞
то, переходя к пределу в равенстве (9) и предполагая функцию ϕ(x)		непрерыв-
ной, найдем:
lim xn = ϕ( lim xn–1).
n→∞	n→∞

В силу (10) получаем

ξ = ϕ(ξ),

т.е. в пределе значения аргумента и функции совпадают. Таким образом, предел ξ является корнем уравнения (1) и может быть вычислен по формуле (9) с любой степенью точности.

Достаточные условия сходимости итерационного процесса дает теорема 3.

Теорема 3. Пусть функция ϕ(x) определена и дифференцируема на отрезке [a; b], причем все ее значения ϕ(x) [a; b]. Тогда, если существует правильная дробь q такая, что

|ϕ ' (x) | ≤ q < 1	(11)
при a < x < b, то:
1) процесс итерации (9) сходится независимо от	начального значения
x0 [a; b];

12

2) предельное значение

ξ = lim xn является единственным корнем уравне-

ния (1) на отрезке [a; b].

n→∞

Для оценки приближения используется формула

ξ − x

≤

qn

x − x

.

(12)

n

1 − q

1

0

Если f(x) = x – ϕ(x), то оценку приближения можно выполнить по формуле

ξ − x

n

≤

q

x

n

− x

n-1

,

1

− q

откуда, в частности, при q = 1

, получаем

2

|ξ – xn| ≤ |xn – xn–1|.

Из последнего неравенства следует, что, если |xn – xn–1| < ε, то и |ξ – xn| < ε. Метод итераций геометрически может быть пояснен следующим образом.

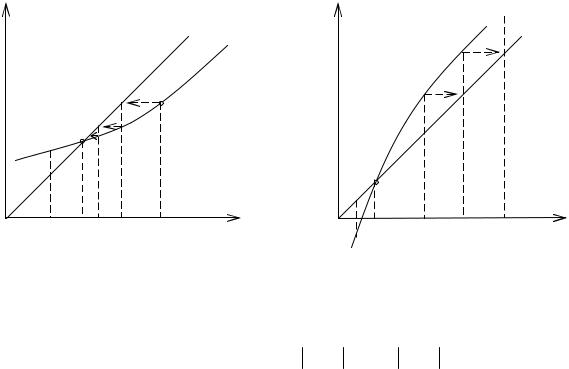
Построим на плоскости xOy графики функций y = x и y = ϕ( x ) . Каждый дейст-

вительный корень ξ уравнения (8) является абсциссой точки М пересечения кривой y = ϕ( x ) с прямой y = x (рис. 3).

Для ϕ ′(x) > 0 и ϕ′( x ) < 1 кривая y = ϕ( x ) пересекает биссектрису y = x (рис. 3а) слева направо и лежит под биссектрисой. Итерационный процесс, начиная с точки x0 монотонно сходится, приближаясь справа к ξ.

′	кривая y = ϕ( x ) находится над биссектрисой y = x , пе-
В случае ϕ ( x ) > 1
ресекая ее слева направо, и процесс монотонно расходится (рис. 3б).
y		y
y=x	y=ϕ(x)	y=ϕ(x)	y=x

M

		M
α ξ x2 x1 x0=β	x	α ξ x0=β x1 x2	x
а		б

Рис. 3. Геометрическая интерпретация итерационного процесса для уравнения x = ϕ( x ) при ϕ′( x ) > 0 .

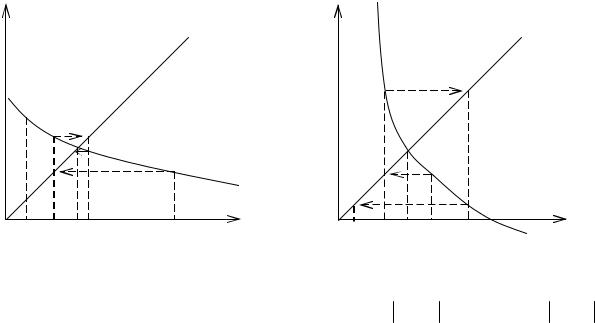
В случае ϕ′(x) < 0 кривые для ϕ′(x) < 1 и ϕ′(x) > 1 приведены на рис. 4 и

представляют соответственно сходящийся и расходящийся процессы с колебаниями вокруг истинного значения корня.

		13
y		y
	y=x	y=ϕ(x)	y=x

y=ϕ(x)

α x1 ξ x2	x0=β	x	x3 x1 ξ x0 x2	x
	а		б

Рис. 4. Геометрическая интерпретация итерационного процесса

для уравнения x = ϕ( x ) при ϕ′( x )< 0: а) – для ϕ ′( x ) < 1; б) – для ϕ′( x ) > 1.

Уравнение (1) можно записать в виде равенства (8), выбирая различным образом функцию y = ϕ( x ) . Для метода итераций выгодно то представление (8),

при котором выполнено неравенство (11), причем, чем меньше q, тем быстрее, вообще говоря, последовательные приближения сходятся к корню (это следует из оценки приближения (12)).

Рассмотрим достаточно общий прием приведения уравнения (1) к виду (8), для которого обеспечено выполнение неравенства (11). Пусть искомый корень ξ уравнения лежит на отрезке [α; β], причем, f '(x)>0 и

0 < m ≤ f '(x) ≤ M

(13)

при α ≤ x ≤ β. В частности, за m можно взять наименьшее значение производной f '(x) на отрезке [α; β], а за M – наибольшее значение f '(x) на отрезке [α; β]. Если производная f '(x) на отрезке [α; β] отрицательна, то вместо уравнения f(x) = 0 рассматриваем уравнение –f(x) = 0. Заменим уравнение (1) эквивалентным ему уравнением

x = x – λf(x), λ > 0.

(14)

Правая часть в полученном уравнении в соответствии с (8) есть функция

ϕ(x)= x – λf(x).

Тогда

ϕ '(x) = 1 – λf '(x).

Подберем параметр λ таким образом, чтобы на интервале [α; β] выполнялось неравенство (11), т.е.

0 ≤ ϕ '(x) = 1 – λf '(x) ≤ q < 1.

Отсюда и на основании неравенства (13) получаем

14

0 ≤ 1 – λM ≤ 1 – λm ≤ q < 1.

Тогда, выбрав

	λ =	1	,	(15)
		M

получим

q = 1 – Mm < 1,

и неравенство (11) выполнено.

Замечания:

1. За число q в теореме 3 можно принять наименьшее значение модуля производной |ϕ ' (x)| при a < x < b.

2. В случае ϕ '(x) < 0 и |ϕ '(x)| < 1 имеет место неравенство

ξ − xn

≤

xn − xn-1

.

(16)

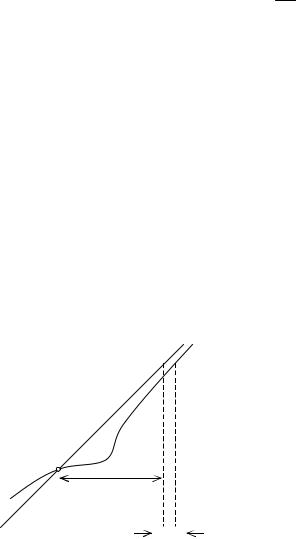
3. В общем случае, из выполнения неравенства |xn – xn–1| < ε не следует вы-

полнение неравенства |ξ – xn| < ε (см. рис.5).

y

y=x

y=ϕ(x)

çξ-xnç

xn

xn-1

x

ε

x

Рис. 5. Пример, что при

xn

- xn-1

< ε имеет место неравенство

ξ - xn

> ε .

4. Упрощенная оценка (16) может быть использована для случая

ϕ '(x) < 0 и

|ϕ '(x)| < 1. Если же ϕ '(x) > 0 и

ϕ '(x) < 1, то, вообще говоря, оценку (16) исполь-

зовать нельзя. Но учитывая, что в этом случае последовательные приближения xn = ϕ(xn–1), n = 1, 2, …, x0 [α; β]

сходится к корню ξ монотонно, можно организовать сужение интервала [α; β], последовательно получая приближения корня с недостатком и избытком. Тогда возможно применение оценки приближения (16).

f ' ( C )

15

1.2.4.1 Алгоритм метода итераций

Вычислительная схема решений имеет вид

xi = x0, x0 [α; β] xi+1 = ϕ(xi), i = 1, 2, …

и сводится к организации циклического процесса с неизвестным числом повторений до выполнения заданного уровня точности, который может быть оценен неравенством (12) или применением упрощенной оценки (16).

Выполним уточнение корня на отрезке [α; β], применив следующий алгоритм.

1.Установить значения α, β, ε – границы отрезка отделения корня и принятую точность приближения.

2.Определить точку (η, M = max| f ' ( x )|).

x [α ; β ]

3.Установить начальное значение x0 [α; β].

4.Вычислить λ = sgn f '(η) M2 .

5.Начать цикл уточнения корня.

5.1.Вычислить очередное приближение x1 = x0 – λf(x0).

5.2.Вычислить d = |x1 – x0|.

5.3.Принять x0 = x1.

6.Конец цикла, если d < ε .

7.Вывод результата x1.

8.Конец алгоритма.

Замечание. Выполнение п.4 алгоритма обеспечивает удовлетворение требований ϕ '(x) < 0 и |ϕ '(x)| < 1, при которых может быть применена упрощенная оценка (16).

1.2.5 Метод Ньютона

Пусть на отрезке [α; β] отделен корень уравнения (1), функция f(x) дважды дифференцируема, а f ′(x) и f ′′(x) сохраняют постоянные знаки на указанном интервале.

В методе Ньютона точное значение ξ корня уравнения (1) заменяется приближенным значением x [α; β], где x – абсцисса пересечения касательной,

проведенной к кривой y = f(x) в точке С [α; β]. Уравнение этой касательной
y – f(С) = f ′(С)(x – С).			(17)
Так как при x = x y = 0, то из (17) получаем
x = С –	f ( C )	.	(18)

16

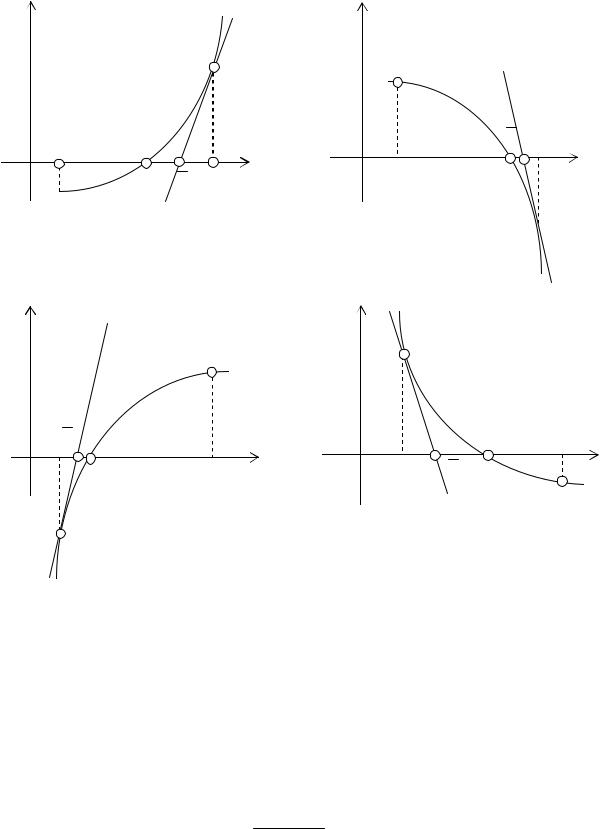
Остается решить вопрос о выборе точки С таким образом, чтобы x [a; b]. Выбор точки С определяется четырьмя случаями, изображенными на рис. 6.

y

f(x)

α

0

ξ x С=β x

1) f ′(x)>0, f ′′(x)>0, C=β, f(C)>0

y

f(x)

x C=β

0	α	ξ	x

2) f ′(x)<0, f ′′(x)<0, C=β, f(C)<0

y

y

f(x)

	α	x				α	ξ	β
0		ξ	β	x	0		x	x

3) f ′(x)>0, f ′′(x)<0, C=α, f(C)<0

Рис. 6

4) f ′(x)<0, f ′′(x)>0, C=α, f(C)>0

Обычно принимают C = a или C = b, смотря по тому, в какой из этих точек знак функции совпадает со знаком второй производной, т.е. выбирают так, чтобы произведение sgn f(C) × sgn f ¢¢ (C) было положительно. Можно показать, что в этом случае a < x < b. Полученное значение x можно использовать для дальнейшего уточнения корня, беря интервал [a; x ] (случаи 1 – 2) или интервал [ x ; b] (случаи

2 – 4).

Геометрический смысл метода Ньютона состоит в замене дуги y = f(x) касательной, проведенной к одной из крайних точек так, что имеет место итерационная формула

xk = xk–1 –	f ( xk −1 )	(k = 1, 2, …),
	f '( xk −1 )

основанная на формуле (18).

17

Для оценки погрешности в методе Ньютона можно воспользоваться форму-

лой

		|xk – ζ| ≤	M	2
				|xk – xk–1| ,
			2m
где m = min	|f ′(x)|, M =	max |f ′′(x)|.
x [α;	β]	x [α;β]

1.2.5.1 Алгоритм метода Ньютона

1.Установить значения α, β, ε – границы отрезка отделения корня и принятую точность приближения.

2.Определить точку (η, M = max | f '' (x) | ).

x [α; β]

3. Вычислить m = min |f '(x)|.

x [α; β]

4. Установить начальное приближение x0 [α; β]:

если sgn f ''(η) = sgn f(α), то x0 = α,

иначе x0 = β.

5.Начать цикл уточнения корня.

5.1.Вычислить очередное приближение x1 = x0 –

5.2.Вычислить d = (x1 – x0)2.

5.3.Принять x0 = x1.

6.Конец цикла, если d < 2Mm ε .

7.Вывод результата x1.

8.Конец алгоритма.

f ( x0 ) . f '( x0 )

1.2.6 Метод хорд

Пусть на отрезке [α; β] отделен корень уравнения (1), функция f(x) дважды дифференцируема, а f ′(x) и f ′′(x) сохраняют постоянные знаки на указанном интервале.

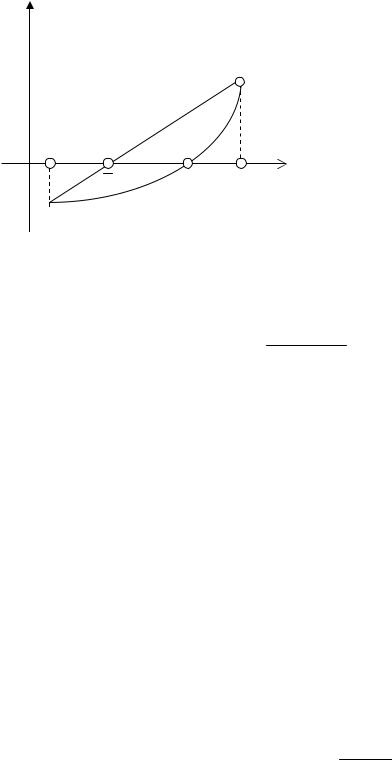
Метод заключается в том, что на интервале [a; b] отделения корня ξ уравнения (1) дуга кривой y = f(x) заменяется стягивающей ее хордой и в качестве приближенного значения корня x принимается точка пересечения хорды с осью абсцисс (рис. 7).

|xn – xn–1| <

18

y

B(b, f(b))

f(b)

	α
0	x	ξ	β x

f(a)

A(a, f(a))

Рис. 7. Геометрическая интерпретация метода хорд

Уравнение хорды определяем как уравнение прямой, проходящей через точки A(a, f(a)) и B(b, f(b)),

имеющее вид

	x − a	=	y − f ( a )		.
	b − a		f ( b ) − f ( a )

(19)

Если x = x , то y = 0, тогда из (19) следует

	x − a	= −	f ( a )		,
	b − a		f ( b ) − f ( a )

откуда находим приближенное значение корня

x = a –	f (a)	(b – a).	(20)
	f (b) − f (a)

Для нахождения последующих приближений определяется отрезок, на концах которого функция имеет разные знаки. Если sgn f(a) = sgn f( x ), то полагается a = x , иначе b = x и повторяются вычисления по формуле (20).

Замечание. Вычисление приближенного значения x корня ξ уравнения (1) выполняется с недостатком, т. е. x – ξ < 0, если на отрезке [a; b] имеют места неравенства:

§f ′(x) > 0 и f ′′(x) > 0 – функция f(x) возрастающая, график f(x) вогнутый;

§f ′(x) < 0 и f ′′(x) < 0 – функция f(x) убывающая, график f(x) выпуклый.

Вычисление приближенного значения x корня ξ уравнения (1) выполняется с избытком, т. е. x – ξ > 0, если на отрезке [a; b] имеют место неравенства:

§f ′(x) > 0 и f ′′(x) < 0 – функция f(x) возрастающая, график f(x) выпуклый;

§f ′(x) < 0 и f ′′(x) > 0 –функция f(x) убывающая, график f(x) вогнутый. Следовательно, сужение интервала изоляции корня возможно изменением

только одной из его границ, а именно, если приближенное значение x корня ξ выполнено с недостатком, то принять a = x , иначе b = x .

Оценить погрешность результата можно, используя следующее соотношение:

m ε, M − m

где m = min	|f ′(x)|, M =	max |f ′(x)|.
x [α;	β]	x [α;β]

1.2.6.1Алгоритм метода хорд

1.Установить значения α, β, ε – границы отрезка отделения корня и принятую точность приближения.

19

2.Выполнить проверку применимости метода: если sgn f(a)= sgn f(b), то метод не применим, конец вычислений. Иначе

3.Установить вариант сужения интервала изоляции корня:

	если sgn f '(a)= sgn f ''(a), то v = 1 – вариант с недостатком
	иначе v = 2 – вариант с избытком.
4.	Вычислить m = min |f ′(x)|; M =	max |f ′(x)|.
	x [α; β]	x [α; β]
5.	Начать цикл уточнения корня.

f(a)

5.1.Вычислить очередное приближение x = a – f (b) − f (a) (b – a).

5.2.Вычислить оценку для приближения и выполнить сужение интервала изоляции корня:

если v = 1, то d = x – a; a = x, иначе d = b – x; b = x.

6. Конец цикла, если d <	m	ε .
	M − m

7.Вывод результата x.

8.Конец алгоритма.

1.2.7Комбинированный метод

Пусть на отрезке [α; β] отделен корень уравнения (1), функция f(x) дважды дифференцируема, а f ′(x) и f ′′(x) сохраняют постоянные знаки на указанном интервале.

Комбинированный метод соединяет в себе метод хорд и метод Ньютона и позволяет на каждом этапе находить значения по недостатку x1 и значения по из-

бытку x2 точного корня ξ уравнения (1). Тогда сужение отрезка изоляции корня можно выполнять, принимая α = x1, β = x2 . Если:

1) f ′(x) > 0 и f ′′(x) > 0 – функция f(x) возрастающая, график f(x) вогнутый или f ′(x) < 0 и f ′′(x) < 0 – функция f(x) убывающая, график f(x) выпуклый, то x1 вычисляется по методу хорд (20), а x2 – по методу Ньютона (18);

2) f ′(x) > 0 и f ′′(x) < 0 – функция f(x) возрастающая, график f(x) выпуклый или f ′(x) < 0 и f ′′(x) > 0 – функция f(x) убывающая, график f(x) вогнутый, то x1 вычисляется по методу Ньютона (18), а x2 – по методу хорд (20).

Погрешность комбинированного метода на n-ом шаге определяется неравенством

|ξ – x | < βn – αn,

где x = 12 (αn + βn).

1.2.7.1 Алгоритм комбинированного метода

1. Установить значения α, β, ε – границы отрезка отделения корня и принятую точность приближения.

Здесь мы приведем программы, написанные на языке BP Pascal 7.0, ния корней уравнений применительно к следующему примеру.

20

2.Выполнить проверку применимости метода: если sgn f(a)= sgn f(b), то метод не применим, конец вычислений. Иначе

3.Установить вариант расчета:

если sgn f ′(a)= sgn f ′′(a), то v = 1

иначе v = 2.

4.Начать цикл уточнения корня.

4.1.Выполнить сужение интервала изоляции корня: если v = 1, то

a = a –		f (a)		(b – a); b = b –			f (b)		,
		f (b) − f (a)					f '(b)
иначе		f (b)				f (a)
b = b –			(b – a); a = a –					.
	f (b) − f (a)				f '(a)

5.Конец цикла, если b – a < ε .

6.Вывод результата x = a +2 b .

7.Конец алгоритма.

1.2.8Программы уточнения корней уравнений

уточне-

Пример. Составить программу на языке BP Pascal 7.0 уточнения корня уравнения

5x − 6x − 3 = 0

(7)

с точностью ε = 10–7, если корни уравнения отделены на отрезках [–1; 0] и [1; 2].

1.2.8.1 Метод половинного деления

program Pdihotomii; uses crt;

const e = 0.0000001; function f(x:real):real;

begin f:=exp(x*ln(5))-6*x-3; end; function sgn(z:real):integer;

begin if z=0 then sgn:=0 else if z>0 then sgn:=1 else sgn:=-1; end; var

a,b,sgna,sgnx,x:real; begin

clrscr;

writeln('Корни отделены на отрезках [-1;0], [1;2]. Введите значения a,b');