2 семестр / ПОСОБИЕ_ВычМат

41

Вприложении MathCAD выполните следующие действия:

1.Введите матрицы А и В с помощью кнопки панели инструментов Matrix

		æ −0.77		−0.04	0.21	−0.18	ö		æ −1.24		ö
		ç	0.45	−1.23	0.06	0	÷		ç	0.88	÷
	A :=	ç					÷	B :=	ç		÷
		ç	0.26	0.34	−1.11	0	÷		ç	−0.62	÷
		ç	0.05	−0.26	0.34	−1.12	÷		ç	1.17	÷
		è					ø		è		ø

2. Вычислите ранг исходной матрицы

rank(A)=4

3.Вычислите ранг расширенной матрицы. Встроенная функция augment(A,B) объединяет две матрицы, имеющие одинаковое количество

строк, в одну

rank(augment(A,B))=4

4. Найдите решение системы матричным методом Х:=А-1×В; 5. Получили результат

é	2.048	ù
ê		ú
ê0.086		ú
x = ê		ú
ê	1.065	ú
ê		ú
ê		ú

ë- 0.65û

6. Найдите решение системы с помощью функции lsolve(А, В)

Х1:=lsolve(А, В)

é	2.048	ù
ê		ú
ê0.086		ú
x1 = ê		ú
ê	1.065	ú
ê		ú
ê		ú
ë- 0.65û
7. Сравните результаты.

Задания к данной теме приведены в приложении Б.

42

3 МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ

3.1 Понятие о приближении функций

Пусть величина y является функцией аргумента x. Вместе с тем на практике часто неизвестна явная связь между y и x, т. е. невозможно записать эту связь в виде некоторой зависимости y = f(x). Наиболее распространенным и практически важным случаем является задание этой связи в виде некоторой таблицы {xi, yi}. Это означает, что дискретному множеству значений аргумента {xi} поставлено в соответствие множество значений функции {yi} (i = 0, 1, …, n). На практике нам могут понадобиться значения величины y в других точках, отличных от узлов {xi}. Этой цели служит задача о приближении функций: данную функцию f(x) требуется приближенно заменить некоторой функцией ϕ(x) так, чтобы отклонение, в некотором смысле, ϕ(x) от f(x) в заданной области было наименьшим. Способы оценки близости приближений порождают различные методы интерполирования и аппроксимации функций.

3.2 Интерполирование функций

Задача интерполирования заключается в следующем. На отрезке [a, b] заданы n+1 точки x0, x1, …, xn, которые называются узлами интерполяции, и значения некоторой функции f(x) в этих точках

f(x0) = y0, f(x1) = y1, …, f(xn) = yn .

Требуется построить функцию ϕ(x) (интерполирующая функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f(x), т. е. такую, что

ϕ(x0) = y0, ϕ(x1) = y1, …, ϕ(xn) = yn.

Геометрически это означает, что нужно найти кривую y = ϕ(x) некоторого определенного типа, проходящую через заданную систему точек Mi(xi, yi) (i = 0, 1, …, n).

Полученную интерполяционную формулу y = ϕ(x) обычно используют для приближенного вычисления значений данной функции f(x) для значений аргумента x, отличных от узлов интерполирования. Если при этом x [x0, xn], то такую операцию называют интерполированием функции f(x), иначе – экстраполировани- ем.

3.2.1 Интерполяционная формула Лагранжа

Пусть на отрезке [a, b] даны n+1 различных значений аргумента: x0, x1, …, xn и известны для y = f(x) соответствующие значения:

f(x0) = y0, f(x1) = y1, …, f(xn) = yn .

Требуется построить многочлен Ln(x) степени не выше n, имеющий в заданных узлах x0, x1, …, xn те же значения, что и функция f(x), т. е. такой, что

43

Ln(xi) = yi (i = 0, 1, …, n).

Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n:

Ln(x) = y0l0(x) + y1l1(x) + …+ ynln(x).

(1)

При этом потребуем, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением одного i-го, где он должен равняться единице. Легко проверить, что этим условиям отвечает многочлен вида

n

Õ( x − x j )

j =0

li(x) = jn¹i , (2)

Õ( xi − x j )

j =0 j ¹i

где i = 0, 1, …, n.

Подставляя в формулу (1) выражение li(x) из формулы (2), находим

		n
		Õ( x − x j )
	n	j =0
		j ¹i
	Ln(x) = å yi			.	(3)
		n
	i=0	Õ( xi − x j )

j =0 j ¹i

Формула (3) определяет интерполяционный многочлен Лагранжа.

Пример 1. Составить алгоритм и программу на языке Turbo Pascal интерполирования функции f(x) на отрезке многочленом Лагранжа по системе 5 узлов в точках: M1(1.05, 2.8577), M2(1.09, 2.9743), M3(1.13, 3.0957), M4(1.15, 3.1582), M5(1.17, 3.2220).

1.Определить исходные данные: число узлов интерполяции n + 1 = 5, вектор абсцисс x = (1,05; 1,09; 1,13; 1,15; 1,17); вектор ординат y = (2.8577, 2.9743, 3.0957, 3.1582, 3.2220).

2.Ввести значение абсциссы C – точку для интерполяции.

n

3. Вычислить значение полинома Лагранжа P = åyk Lk .

k=0

3.1.Присвоить P = 0.

3.2.Организовать цикл, изменяя параметр k = 0, 1, ..., n.

n	n
3.2.1. Вычислить значение Lk = Õ( C − x j ) / Õ( xk − x j ).
j=0	j=0
j¹k	j¹k

3.2.1.1. Определить Lk = 1.

44

3.2.1.2.Организовать цикл, изменяя параметр j = 0, 1, ..., n.

3.2.1.2.1.Если j¹k вычислить Lk = Lk*(C–xj)/(xk – xj).

3.2.1.3.Конец цикла по параметру j.

3.2.2. Вычислить P = P + yk * Lk. 3.3. Конец цикла по параметру k.

4.Вывод результата P – значение полинома Лагранжа в точке x = C.

5.Конец вычислений.

Программа интерполирования функции полиномом Лагранжа

Program Lagrang; uses crt;

const n=4;

{описание узлов интерполяции}

x:array[0..n] of real = (1.05, 1.09, 1.13, 1.15, 1.17); y:array[0..n] of real = (2.8577, 2.9743, 3.0957, 3.1582, 3.2220); var

k,j:byte;

P,L,c:real; begin

writeln('Введите значение х - точку для интерполирования'); readln(c);

P:=0; {для результата интерполирования}

{вычисление значения полинома Лагранжа в точке x=c} for k:=0 to n do

begin L:=1;

for j:=0 to n do if j<>k then

L:=L*(c-x[j])/(x[k]-x[j]); P:=P+y[k]*L;

end;

write('x=',c:7:2,' P=',P:7:4);

writeln(', табличное значение=',exp(c):7:4); readkey;

end.

3.2.2 Интерполяционные формулы Ньютона

Рассматриваемые здесь интерполяционные формулы Ньютона используются в случае равноотстоящих значений аргумента, т. е. xi+1 – xi = h = const (i = 0, 1, ..., n). Величина h называется шагом.

Введем понятие конечных разностей. Пусть функция y = f(x) задана табличными значениями yi = f(xi) для системы равноотстоящих точек xi.

Разностями первого порядка функции называются выражения вида

45

∆yi = yi+1 – yi (i = 0, 1, …, n–1).

Разностями второго порядка функции называются выражения вида

∆2yi = ∆(∆yi )= ∆yi+1 – ∆yi (i = 0, 1, …, n–1).

Аналогично составляются разности порядка k

∆kyi = ∆(∆k–1yi )= ∆k–1yi+1 – ∆k–1yi (i = 0, 1, …, n–1).

Отметим, что для вычисления k-ой разности ∆kyi нужно знать k+1 членов y: yi+1, ...

yi+k данной последовательности.

Перейдем теперь к построению интерполяционного многочлена Ньютона. В соответствии с задачей интерполирования функции требуется подобрать многочлен Pn(x) степени не выше n, принимающий в точках xi значения

Pn(xi) = yi (i = 0, 1, …, n).	(4)
Этот многочлен будем искать в следующем виде:
Pn(x) = a0 + a1(x–x0)[1] + a2(x–x0)[2] + …+ an(x–x0)[n],	(5)
где
(x – x0)[k] = (x – x0)(x – x1)...(x – xk–1).

Задача состоит в определении коэффициентов ak (k = 0, 1, …n) многочлена Pn(x). Полагая в формуле (5) x = x0, получаем

Pn(x0) = a0,

откуда, с учетом значения многочлена (4), a0 = y0.

Полагая в формуле (5) x = x1, получаем

Pn(x1) = a0 + a1(x1 – x0) = a0 + a1h = y1,

откуда

	a1 =	y1 − a0	=	y1 − y0	=	y0 .
		h		h
						h

Полагая в формуле (5) x = x2, получаем

Pn(x2) = a0 + a1(x2 – x0) + a2(x2 – x0)(x2 – x1) = a0 + 2a1h + 2a2h2 = y2,

откуда

		y2 − a0 − 2a1h		y2	− y0 − 2	y0	h		2	y0
a2	=		=			h		=			.
		2h2			2h2
									2h2

Аналогично можно найти и другие коэффициенты. Общая формула имеет вид

ak =	k y	(k = 0, 1, …, n).
	0
	k!hk

46

Подставляя найденные значения коэффициентов ak (k = 0, 1, …n) в выражение (5),

получаем первую интерполяционную формулу Ньютона:

Pn(x)=y0+

y

(x–x0)

[1]

+

2 y

(x–x0)

[2]

+...+

n y

(x–x0)

[n]

.

(6)

0

0

0

1! h

2! h2

n! hn

Для практического использования интерполяционную формулу Ньютона (6) обычно записывают в виде формулы (7), для чего вводится новая переменная

q = x − x0 , h

представляющая собой число шагов, необходимых для достижения точки x, исходя из точки x0. Тогда

Pn(x) = Pn(x0 + qh) = y0 + q∆y0 + q( q − 1) ∆2y0 + ...

2!

	+	q( q − 1)...( q −( n −1))		∆ny0.	(7)
		n!

Первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад.

Если разности вычислять справа налево, то в этом случае

q = x − xn , h

т. е. q < 0 и интерполяционный многочлен Ньютона можно получить в виде

Pn(x) = Pn(xn + qh) = yn + q∆yn-1 + q( q + 1) ∆2yn-2 + ...

2!

	+	q( q + 1)...( q + ( n − 1))		∆ny0.	(8)
		n!

Формула (8) называется вторым интерполяционным многочленом Ньютона

и обычно используется для интерполирования в конце таблицы, т. е. в правой половине отрезка [x0, xn], и экстраполирования вперед.

Погрешность вычисления при интерполировании по формулам Ньютона оценивается остаточным членом:

– для первой формулы

≈ q( q − 1)...( q − n ) Rn(x) +

( n 1)!

– для второй формулы

≈ q( q + 1)...( q + n ) Rn(x) +

( n 1)!

n+1 y0 ;

n+1 yn ,

где предполагается, что n+1y почти постоянны для функции y = f(x) и h – достаточно мало.

47

Замечание. В практических задачах возможна ситуация, когда Dkyi = 0, для некоторого 1< k £ n. Тогда степень полинома равна k–1 < n.

3.2.2.1 Алгоритмы интерполирования многочленами Ньютона

Рассматриваемые алгоритмы интерполирования основаны на формулах (7) и

(8). Для вычисления разностей различных порядков удобно использование следующего рекуррентного соотношения:

Dny =	ì	yi ,	если n = 0,	(9)
i	í		- Dn−1 yi , если n > 0.
	îD( Dn−1 yi ) = Dn−1 yi+1

Заметим также, что множитель
	q( q − 1)( q − 2 )...( q − ( i − 1))		(10)
	i!

в i-ом слагаемом формулы (7) может быть вычислен с использованием предыдущего множителя, а именно

q( q − 1)( q − 2 )...( q −( i − 2 )) × q −( i − 1) . ( i - 1)! i

1444442444443

предыдущий множитель

Аналогичное соотношение имеет место в формуле (8).

Алгоритм расчета по первой интерполяционной формуле Ньютона

1.Ввести значения: n (n+1 – число узлов интерполяции), x0 – начальное значение аргумента, h – шаг интерполирования, yi (i = 0, 1, …, n) –значение функции в i-ом узле интерполяции, x – значение аргумента для интерполирования функции.

2.Вычислить q = (x – x0)/h.

3.Вычислить Pn(x) = y0 – учитываем первое слагаемое в формуле (7).

4.Определить p = 1.

5.Организовать цикл интерполирования, изменяя параметр i =1, 2, … n.

5.1. Вычислить p = p× q −( i − 1) – множитель (10). i

5.2.Вычислить Diy0 по формуле (9).

5.3.Вычислить Pn(x) = Pn(x) + p×Diy0 – суммирование i-го слагаемого в фор-

муле (7).

6.Конец цикла интерполирования по параметру i.

7.Вывод x – значение аргумента, Pn(x) – результат интерполирования функции.

8.Конец вычислений.

Алгоритм расчета по второй интерполяционной формуле Ньютона можно получить модификацией вышеописанного алгоритма, в частности:

1.Вычислить q = (x – xn)/h, где xn = x0 + nh.

2.Вычислить Pn(x) = yn.

48

2.1. Вычислить p = p× q + ( i − 1) . i

2.2.	Вычислить iyn-i.
2.3.	Вычислить Pn(x) = Pn(x) + p × iyn-i.

Пример 2. Составить программы на языке Turbo Pascal интерполирования функции f(x) на отрезке многочленами Ньютона по системе 5 узлов в точках: M1(1.05, 2.8577), M2(1.09, 2.9743), M3(1.13, 3.0957), M4(1.17, 3.2220), M5(1.21, 3.3535).

{первая интерполяционная формула Ньютона} program pNuton1;

uses crt; const

n = 4; {число узлов интерполяции, счет от нуля} type

Tmas = array[0..n] of real;

{*******функция вычисляет k-ю разность yi} function fdelta( var y : Tmas; i, k : byte) : real; begin

if k = 0 then fdelta := y[i] else fdelta := fdelta(y, i+1, k-1) - fdelta(y,i,k-1) end;

{основная программа} const

y : Tmas = (2.8577, 2.9743, 3.0957, 3.2220, 3.3535); var

i : byte; x0 , x , h , p , pn : real; delta, q : real; begin

x0:=1.05; h := 0.04;

writeln('Введите значение аргумента x для выполнения интерполяции'); readln(x);

pn:=y[0]; q:=(x-x0)/h; p:=1;

for i:=1 to n do {цикл интерполирования}

begin p:=p*(q-(i-1))/i; delta:=fdelta(y,0,i); pn:=pn+p*delta; end; writeln('Для значения x = ', x:12:5, ' получен результат Pn =', pn:12:5 ); writeln('Точное значение: ', exp(x):12:5);

readkey;

end.

{вторая интерполяционная формула Ньютона} program pNuton2;

uses crt; const n=4;

type Tmas=array[0..n] of real; {*******функция вычисляет k-ю разность yi}

49

function fdelta( var y:Tmas;i,k:byte):real; begin

if k = 0 then fdelta := y[i] else fdelta := fdelta(y, i+1, k-1) - fdelta(y, i, k-1) end;

{основная программа} const

y : Tmas = (2.8577, 2.9743, 3.0957, 3.2220, 3.3535); var

i : byte; x0, x, h, p, pn, delta, xn, q : real; begin

h:=0.04; x0:=1.05;

writeln('Введите значение аргумента x для выполнения интерполирования'); readln(x);

pn := y[n]; xn := x0 + n*h; q := (x-xn)/h; p:=1; for i:=1 to n do

begin

p:=p*(q+(i-1))/i; delta:=fdelta(y,n-i,i);{вычисляет i-ю разность y[n-i]} pn:=pn+p*delta;

end;

writeln('x=',x:12:5,' Pn =',pn:12:5); writeln('Точное значение = ',exp(x):12:5); readkey;

end.

3.2.3 Интерполирование функций средствами MachCAD

Система MathCAD предоставляет возможность интерполяции функций с помощью сплайнов. При сплайн-интерполяции исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках.

Для осуществления сплайновой интерполяции предлагается четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:

§cspline (X, Y) – возвращает вектор S вторых производных при приближении в опорных точках к кубическому полиному;

§pspline (X, Y) – возвращает вектор S вторых производных при приближении в опорных точках к параболической кривой;

§lspline (X, Y) – возвращает вектор S вторых производных при приближении в опорных точках к прямой.

Четвертая функция - interp (S, X, Y, z) – возвращает значение у(х) для заданных векторов S, X, Y и заданного значения z.

Выполните в системе MachCAD следующие действия:

1. Организуйте данные в виде отсортированных соразмерных векторов:

	50
X := (1.05 1.09 1.13 1.15 1.17 )T	Y := (2.8577 2.9743 3.0957 3.1582 3.222 )T

2. Задайте вектор вторых производных при помощи одной из приведенных выше функций семейства *spline, например lspline:

s1 := lspline(X ,Y)

é	0	ù
ê	3	ú
ê		ú
ê		ú
ê	0	ú
ê		ú
ê	0	ú
s1 = ê		ú
ê3.875ú
ê		ú
ê	2.5	ú
ê		ú
ê	4.25	ú
ê		ú
ê	0	ú
ë		û

3.Задайте функцию interp(s1,x,y, z). В нашем случае:

I1(Z) := interp(lspline(X ,Y) , X ,Y ,Z)

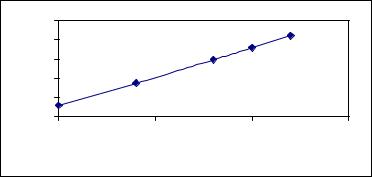
4.Постройте график, выбрав пиктограмму на панели Graph. Пропишите в соответствующих маркерах имя функции интерполяции и переменную. Получили сплайн-интерполяцию с линейным продолжением:

	3,3
	3,2
I1	3,1
	3
	2,9
	2,8
	1,05	1,1	1,15	1,2
			Z,X

5.Аналогичным образом постройте сплайн-интерполяцию, используя функции cspline, pspline. Сравните результаты.

Задания к данной теме приведены в приложении В (1).