2 семестр / ПОСОБИЕ_ВычМат

61

4.3.2 Программа на языке Turbo Pascal для вычисления первой и второй производной функции

program p1p2; uses crt;

var a,b,x,h,y1,y2:real; i,n:integer;

y:array [0..200] of real; begin

clrscr;

writeln('Введите значения a, b, x и число разбиений отрезка [a, b]'); readln(a,b,x,n);

writeln(' введите значения функции в узлах интерполяции '); for i:=0 to n do

readln(y[i]); h:=(b-a)/n; i:=trunc((x-a)/h+h/2); if i = 0

then begin

y1:=(-3*y[0]+4*y[1]-y[2])/(2*h); y2:=(2*y[0]-5*y[1]+4*y[2]-y[3])/sqr(h); end

else

if i<>n then begin

y1:=(-y[i-1]+y[i+1])/(2*h); y2:=(y[i-1]-2*y[i]+y[i+1])/sqr(h); end

else{i=n} begin

y1:=(y[n-2]-4*y[n-1]+3*y[n])/(2*h); y2:=(-y[n-3]+4*y[n-2]-5*y[n-1]+2*y[n])/sqr(h); end;

writeln('x=',x:12:6,' y1=',y1:12:6,' y2=',y2:12:6); readkey;

end.

62

4.3.3 Вычисления первой и второй производной функции средствами

MS Excel

Формулы для вычисления первой и второй производной функции:

	A	B	C	D	E	F	G
1	a	b	x	n	h	I	y
2	2,4	4,6	4,13	8	=(B2-A2)/D2	=ЦЕЛОЕ((C2-A2)/E2+E2/2)	3,53
3							3,78
4							3,95
5							4,04
6							4,12
7							4,16
8							4,25
9							4,37
10							4,51

									H
	1								y1
	2	=ЕСЛИ(F2=0;(-3*G2+4*G3-G4)/(2*E2);ЕСЛИ(F2<>D2;(-G7+G9)/(2*E2);(G8-4*G9+3*G10)/(2*E2)))
	3
									I
	1								y2
	2	=ЕСЛИ(F2=0;(2*G2-5*G3+4*G4-G5)/(E2^2);ЕСЛИ(F2<>D2;(G7-2*G8+G9)/(E2^2);(-G7+4*G8-
		5*G9+2*G10)/(E2^2)))
	3
	Результат вычисления производных:
			A	B		C	D		E		F	G	H	I
	1		a	b		x	n		h		I	y	y1	y2
	2		2,4	4,6		4,13	8		0,338		5	3,53	0,311111	0,263374
	3											3,78
	4											3,95
	5											4,04
	6											4,12
	7											4,16
	8											4,25
	9											4,37
	10											4,51

Задания к данной теме приведены в приложении Г.

xi-1/2 =

63

5 ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Если функция f(x) непрерывна на отрезке [a, b] и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница:

b

ò f (x)dx = F(b)–F(a),

a

где F′(x) = f(x).

Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление определенного интеграла называется механиче-

ской квадратурой, а соответствующие формулы – квадратурными формулами.

Обычный прием механической квадратуры состоит в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей (аппроксимирующей) функцией ϕ(x) простого вида, например, полиномом, а затем приближенно полагают

b	b
ò f ( x )dx = òϕ( x )dx .		(1)
a	a

Функция ϕ(x) должна быть такова, чтобы интеграл в правой части формулы (1) вычислялся непосредственно. В зависимости от вида функции ϕ(x), интерполирующей подынтегральную функцию, будем получать различные квадратурные формулы.

5.1 Квадратурная формула прямоугольников

Для приближенного вычисления определенного интеграла (1) разобьем отрезок интегрирования [a, b] на n равных частей точками:

x0 = a,

x1 = x0+h,

...

xi = xi-1+h,

...

xn = b,

где h – шаг разбиения, h = b −n a .

Значение функции в точках разбиения xi обозначим через yi. Если теперь на каждой части [xi-1, xi], i = 1, 2, ..., n деления отрезка [a, b] функцию f(x) заменить функцией, принимающей постоянное значение, равное значению функции f(x) в серединной точке i-ой части

xi−1 + xi , 2

то функция ϕ(x) будет иметь ступенчатый вид (рис. 1):

64

y	ϕ(x)
yi	f(x)
yi-1/2
yi-1

xi-1

xi-1/2

xi

xi+1/2

xi+1

х

Рис. 1

ϕ(x) = ϕi(x) = yi-1/2 = f(xi-1/2), x [xi-1, xi], i =1, ..., n.

В этом случае

b	n	xi	n
òϕ( x )dx = å		ò	ϕi( x )dx = åhyi−1 / 2
a	i=1 xi −1		i=1
и получаем квадратурную формулу прямоугольников
b			n−1
In = ò f ( x )dx ≈ h(y1/2 + y3/2 + ... + yi-1/2 + ... + yn-1/2)=h å yi+1 / 2				(2)
a			i=0

5.2 Квадратурная формула трапеций

Квадратурную формулу трапеций получают, если функцию f(x) на каждом отрезке [xi-1, xi] заменить ее линейной интерполяцией по точкам (xi-1, yi-1) и (xi, yi). Тогда

	ϕ(x) = ϕi(x) = yi-1	xi − x	+ yi	x − xi −1	, x [xi-1, xi], i = 1, 2, ..., n,	(3)
		h		h

где yi = f(xi).

Графиком этой функции является ломаная линия (рис. 2).

y

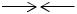h h

xi-1

xi

xi+1

x

Рис. 2

65

В этом случае

b

n

xi

òj(x)dx = å

òji (x)dx.

a

i=1 xi−1

Так как с учетом формулы (3) имеем:

x

x

xi - x

x - xi−1

òiϕi (x)dx = òi

(yi−1

+ yi

)dx =

xi−1

xi−1

h

h

=

yi−1

(x x -

x2

)

xi

+

yi

(

x2

- x

−1

x)

xi

=

h

i

2

xi−1

h 2

i

xi−1

=

yi−1

((x2

-

xi2

) - (x x

-

xi2−1

)) +

yi

((

xi2

- x

i

−1

x

) - (

xi2−1

- x2

)) =

h

i

2

i i −1

2

h

2

i

2

i−1

y

i−1

x2

x2

y

i

x2

x2

=

(

i

- x x

i−1

+

i−1

) +

(

i

- x

x +

i

−1

)

h

2

i

2

h

2

i

−1

i

2

и, учитывая, что

h2

)2

x2

x2

(x - x

=

i

i

−1

=

i

– xixi–1 +

i

−1

,

2

2

получаем

2

2

x

yi−1

h2

yi

h2

yi −1 + yi

òiϕi (x)dx =

+

=

h.

2

xi−1

h

h

2

2

Следовательно,

b

n

y

i −1

+ y

i

òϕ(x)dx = å

× h,

a

i=1

2

и получаем квадратурную формулу трапеций

b		+ yn		y0	+ yn	n−1
Iт = ò f (x)dx » h(	y0		+ y1 + y2 + ... + yn-1)= h(			+ å yi )	(4)
		2			2
a						i =1

5.3 Квадратурная формула парабол (Симпсона)

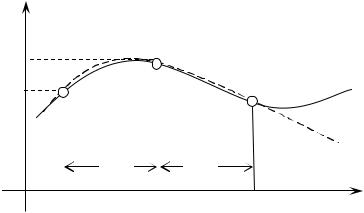
Выполним интерполирование подынтегральной функции полиномом Лагранжа P2(x) второго порядка. На отрезке [xi-1, xi] интерполяционный полином, представляющий собой параболу (рис. 3), будет иметь вид:

P2(x) = ϕi(x) = yi–1	(x − xi−1/ 2 )(x − xi )				+
	(x	- x	)(x	- x )
	i−1	i−1/ 2	i−1	i

66

+ y

(x − xi−1)(x − xi )

+ y

(x − xi−1)(x − xi−1/ 2 )

=

i−1/ 2 (x

−1/ 2

- x

)(x

- x )

i (x - x

)(x - x

)

i

i−1

i−1/ 2

i

i i−1

i

i−1/ 2

= yi−1

(x − xi−1/ 2 )(x − xi )

+ yi−1/ 2

(x − xi−1)(x − xi )

+ yi

(x − xi−1)(x − xi−1/ 2 )

=

-

h

× (-h)

h

× (-

h

)

h ×

h

2

2

2

2

= yi −1

2(x − xi −1/ 2 )(x − xi )

+ yi−1/ 2 − 4(x − xi−1)(x − xi ) + yi

2(x − xi−1)(x − xi−1/ 2 )

,

h2

h2

h2

где x [xi–1, xi],

xi–i/2 =

xi−1 + xi

, i = 1, 2, ..., n.

y

2

yi-1/2

f(x)

yi-1

ϕ(x)

h/2

h/2

xi-1

xi-1/2

xi

x

Рис. 3

Для дальнейших преобразований введем переменную t Î [0, 1] и с помощью равенства x = xi–1+ht выразим ϕi(x) через новую переменную t

~

2( xi−1 + ht − xi−1/ 2 )( xi−1

+ ht − xi )

ϕi(x) = ϕ i(t) = yi−1

+ yi−1/ 2 ´

h2

´ − 4(xi−1 + ht − xi −1)(xi−1 + ht − xi )

+ yi

2(xi −1 + ht − xi−1)(xi−1 + ht − xi −1/ 2 )

=

h2

h2

h

h

2(ht -

)(ht - h)

- 4ht(ht - h)

2ht(ht -

)

= yi −1

2

+ yi−1/ 2

+ yi

2

= yi −1(2t -1)(t -1) +

h2

h2

h2

+ yi −1/ 2 (-4t(t -1)) + yit(2t -1) = yi−1(1 - t)(1 - 2t) + 4yi−1/ 2t(1 - t) + yit(2t -1) =

= yi−1(1 - 3t + 2t2 ) + 4yi−1/ 2 (t - t2 ) + yi (2t2 - t), i = 1, 2, ..., n.

Учитывая, что

67

1	(1 - 3t + 2t2 )dt = t -											3t2											2t3						1							3			2			1
ò																			+										0			=1			-			+			=		,
													2											3												2			3			6
0
1	(t - t2 )dt =			t2			t3				1						1							1					1
ò						-					0		=								-					=							,
				2			3										2							3					6
0
1	(2t2	- t)dt =			2t3				t2							1					2						1							1
ò							-									0	=							-								=			,
						3		2													3						2							6
0
имеем																							x = xi−1 + ht
		n xi
b																								dx = h × dt																		n		1	~	n	h
òj( x )dx = å òji ( x )dx =																																									= åhòji ( t )dt = å							( yi−1	+ 4 yi−1 / 2	+ yi )
																		x = x														при t = 0															6
a		i=1	xi−1																																						i=1			0		i =1
																									i−1
																				x = xi при															t = 1

В результате приходим к квадратурной формуле парабол (формуле Симпсона):

	b	h	n−1
	Ic = ò f (x)dx »		(y0 + yn + 4å yi +1/ 2
		6
	a		i=0

n−1
+ 2å yi ).	(5)

i =1

Приближенное значение интеграла, Ic, вычисленное по квадратурной формуле парабол (5), можно выразить через значения In и IT – результаты вычислений по квадратурным формулам прямоугольников (2) и трапеций (4):

	Ic =	4In + 2IT	=	2In + IT	.	(6)
		6		3

5.4 Оценка погрешностей квадратурных формул

Для оценки погрешности квадратурных формул потребуем, чтобы подынтегральная функция имела непрерывную производную до четвертого порядка. Тогда:

для формулы прямоугольников

R(h) £ h

2

×

b − a

max

f '' ( x )

=

( b - a )3

max

f '' ( x )

;

(7)

24

24n2

a≤x≤b

a≤x≤b

для формулы трапеций

R(h) £ h

2

×

b − a

max

f '' ( x )

=

( b - a )3

max

f '' ( x )

;

(8)

12

12n2

a≤x≤b

a≤x≤b

In - I2n < ε,

68

для формулы Симпсона

( b - a )5

R(h) ≤ n ×

h5

max

f ( 4 )( x )

=

max

f ( 4 )( x )

;

(9)

180( 2n )4

где h =

b − a

.

90 a≤x≤b

a≤ x≤b

2n

5.5 Метод двойного пересчета

Следует отметить, что практическое значение оценок (7)-(9) невелико ввиду сложности их использования. Поэтому при численном интегрировании прибегают к другим приемам. В частности, вычисляют интегралы по квадратурным формулам (2), (4), (5) при делении отрезка на n частей и 2n частей. Если получающиеся значения обозначить соответственно через In и I2n, то совпадение первых знаков In и I2n позволяет судить о точности полученных значений. Чтобы определить, как сильно уклоняется значение I2n от точного значения интеграла I, используется правило Руни:

I - I2n » 2k 1- 1 In - I2n ,

где k=2 для формул прямоугольников и трапеций и k=4 для формулы Симпсона. При заданной e точности вычисления с уменьшающимся шагом следует

прекратить, если

1

2k - 1

при этом полагают, что I » I2n с точностью e.

5.6 Алгоритм вычисления интегралов по формулам прямоугольников, трапеций и Симпсона

1. Определить исходные данные: a – начало интервала интегрирования; b – конец интервала интегрирования;

n– число частей разбиения.

2.Вычислить шаг интегрирования h = (b – a) / n.

3.Вычислить начальные значения интегральных сумм: Ip:=f(a+h/2) – для метода прямоугольников, It:=(f(a)+f(b))/2 – для метода трапеций.

4.Организовать цикл накопления подынтегральной суммы, изменяя значения параметра цикла i от 1 до n - 1 с шагом 1.

5.Вычислить: Ip:=Ip+f(a+h*(i+1/2)) – интегральную сумму метода прямоугольников, It:=It+f(a+i*h) – интегральную сумму метода трапеций.

6.Выполнить вывод результатов: h*Ip – значение интеграла, вычисленное по методу прямоугольников, h*It – значение интеграла, вычисленное по методу трапеций, h/6*(4*Ip+2*It) – значение интеграла, вычисленное по методу Симпсона.

69

7. Конец вычислений.

π / 2

Пример. Вычислить интеграл òcos x dx

0

по формулам прямоугольников, трапеций и Симпсона, если отрезок интегрирования разбит на n равных частей. Сравнить приближенные значения интеграла с точными.

Вычисления производятся по формулам (2), (4), (6).

5.7 Программа на языке Turbo Pascal для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона

program pIPTS; uses crt;

function f(x:real):real; {вычисление значений подынтегральной функции} begin

f:=cos(x);

end;

var a,b,h,Ip,It,Is:real; i,n:integer;

begin a:=0;b:=pi/2;n:=100;

h:=(b-a)/n; {шаг интегрирования} Ip:=f(a+h/2); {для метода прямоугольников} It:=(f(a)+f(b))/2;{для метода трапеций}

for i:=1 to n-1 do begin {цикл накопления подынтегральной суммы} Ip:=Ip+f(a+h*(i+1/2));{интегральная сумма метода прямоугольников} It:=It+f(a+i*h); {интегральная сумма метода трапеций}

end;

clrscr;

writeln('Значение интеграла метода прямоугольников= ',h*Ip:17:9); writeln('Значение интеграла метода трапеций= ',h*It:17:9); writeln('Значение интеграла метода Симпсона= ',h/6*(4*Ip+2*It):17:9); writeln('Контроль = ',sin(pi/2):12:9);

readkey; end.

70

5.8 Вычисление интегралов по формулам прямоугольников, трапеций и парабол средствами MS Excel

Формулы для вычисления интегралов по формулам прямоугольников, трапеций и парабол:

	A	B		C	D	E	F
1	a	b		n	h	Ip0	It0
2	0=ПИ()/2			100	=(B2-A2)/C2	=COS(A2+D2/2)	=(COS(A2)+COS(B2))/2
3
4
5					I	Ip	It
6					=D6+1	=E6+COS($A$2+$D$2*(D6+1/2))=F6+COS($A$2+D6*$D$2)
7				интегральная сумма		=E2+E6	=F2+F6
8
9			значения интегралов
10		прямоугольник		трапе-	парабола	контроль
				ция
11		=D2*E7		=D2*F7	=D2/6*(4*E7+2*F7)	=SIN(ПИ()/2)

Для вычисления формул необходимо установить предельное число итераций 99 (с помощью команды меню Сервис/ Параметры/ Вычисления).

Результат вычисления интегралов:

	A	B	C	D	E	F
1	a	b	n	h	Ip0	It0
2	0	1,570796327	100	0,015707963	0,999969158	0,5
3
4
5				I	Ip	It
6				99,00	62,66266258	63,16066823
7			интегральная сумма		63,66263174	63,66066823
8
9		значения интегралов
10		прямоугольник	трапеция	парабола	контроль
11		1,000010281	0,999979438	1	1