§13. Статистический метод исследования систем. Понятие о случайной величине и функции распределения

Для описания совокупности большого числа хаотически движущихся частиц предполагается, что каждая частица движется по законам механики. Однако было бы бесполезно пытаться описать свойства этой системы методами механики ввиду чрезвычайно большого числа частиц, входящих в данную систему (в 1 см³ газа содержится ~10¹⁹ молекул).

Кроме того, подобная система имеет такие свойства, которых нет у отдельных частиц (например, давление). В связи с этим для описания системы частиц требуются иные методы, отличные от методов механики.

Основная задача молекулярной (статистической) физики заключается в установлении связи макроскопических свойств системы со свойствами и законами движения микрочастиц, составляющих систему.

Для решения поставленной задачи используется математическая теория вероятностей, которая была разработана для массовых явлений, например, таких, в которых участвует большое число частиц. Метод описания, использующий теорию вероятностей, называют статистическим методом, а закономерности, выявляемые с помощью этого метода - статистическими закономерностями. Этот метод оперирует некоторыми специальными понятиями, из которых при изучении молекулярно-кинетической теории будут использоваться следующие: случайная величина, вероятность распределения, среднее значение случайной величины.

Случайными величинами называются величины, которые меняют свое значение от испытания к испытанию, от случая к случаю.

Для изучения физических явлений производят наблюдения и опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов (например, при измерении температуры тела). В этом случае говорят, что результат измерения есть величина случайная.

Различают дискретные и непрерывные случайные величины. Дискретной случайной величиной будет число молекул в некоторой малой области газа из его общего объема, так как оно будет меняться со временем и принимать только значения целых положительных чисел. В качестве непрерывной случайной величины можно привести скорость молекулы газа. Это векторная случайная величина, модуль которой может принимать любые значения от нуля до бесконечности и которая может иметь самые различные направления.

Случайная величина может принимать разные числовые значения. Например, при неоднократном измерении длины стержня с помощью штангенциркуля в общем случае получатся хотя и близкие, но все-таки различные результаты. Одинаковые результаты могут иногда повторяться. В теории вероятности принято называть появление того или иного результата при многократных испытаниях случайным событием, а количественно характеризовать его совершение - вероятностью.

Пусть случайная величина была измерена раз, при этом численное значениеповторилось раз, -раз и т.д. Отношение называют относительной частотой совершения случайного события , то есть появления результата, а предел этого отношения при устремлениик бесконечности - вероятностью () данного случайного события:

_.

Иногда под вероятностью понимают само отношение , подразумевая, что .

Функцией распределения называют некоторое математическое выражение (с соответствующим графическим отображением), определяющее относительную долю числа частиц (от общего их числа в веществе), приходящихся на единичный диапазон изменения какой-либо случайной величины.

Если обозначить через общее число частиц, а через- число частиц, приходящихся на интервализменения некоторой случайной величины, то функция распределения числа частиц вещества по значениям случайной величины будет иметь вид

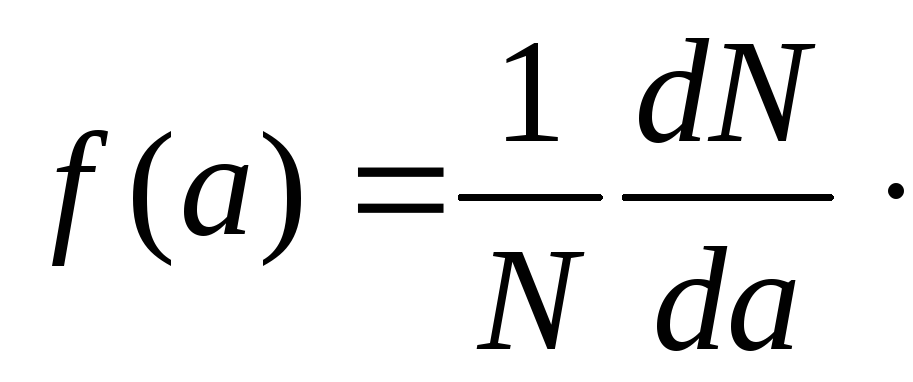(13.1)

Рассмотрим пример, иллюстрирующий смысл функции распределения.

Рис.13.1

Пусть в ящик, разделенный перегородками на ряд узких отсеков (рис.13.1) одинаковой ширины и закрытый несколькими слоями металлической сетки, через воронку насыпается мелкий сухой песок. Падая из воронки, песчинки будут неоднократно ударяться о сетку и отклоняться от первоначального направления движения. Вследствие случайных отклонений песчинка может попасть в любой из отсеков. Тем не менее, в распределении частиц по отсекам имеется закономерность: во всех опытах в отсек под воронкой попадает наибольшее число песчинок, а по мере удаления от этого отсека число песчинок в отсеках уменьшается.

Рис 13.2.а

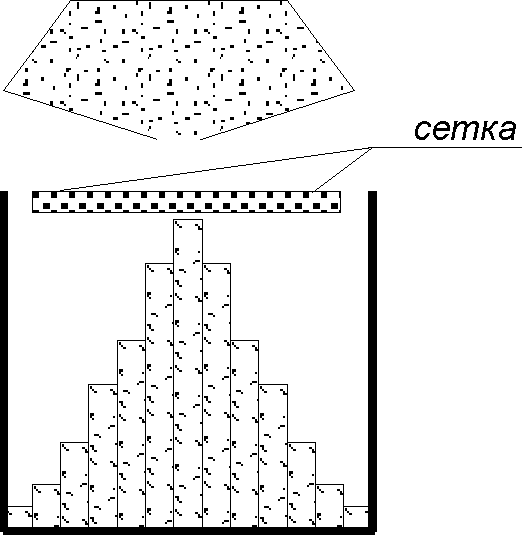
На рис.13.2.а изображена ступенчатая диаграмма распределения песчинок по отсекам: - число песчинок (из общего их числа) в одном из отсеков шириной; отношение- это число песчинок, приходящихся на единицу длины, следовательно, площадь каждого прямоугольника численно равна числу песчинок, содержащихся в данном отсеке (), а площадь фигуры, образованной диаграммой и осью , равна общему числу песчинок в ящике ().

В рассмотренном примере имеется распределение песчинок по координате . Случайной величиной является отклонение частиц от средней точки0 (то есть координата ).

Рис.13.2.б

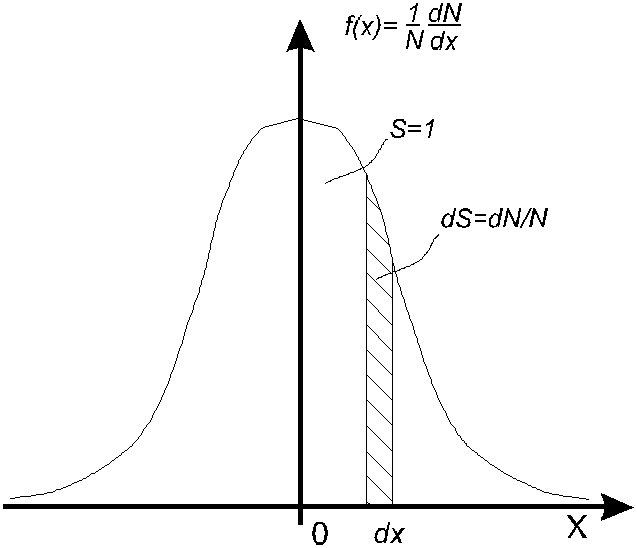
При уменьшении ширины отсека (в пределе ) ступенчатая ди-аграмма перейдет в плавную линию, при этом, если по оси ординат откладывать значения, то площадь фигуры под кривой

распределения (рис.13.2.б) будет равна единице ().

Одной из важнейших характеристик статистических распределений является среднее значение случайной величины. Дадим определения среднему арифметическому и среднему квадратичному значениям случайной величины.

Среднее арифметическое значение случайной величиныопределяется из соотношения:

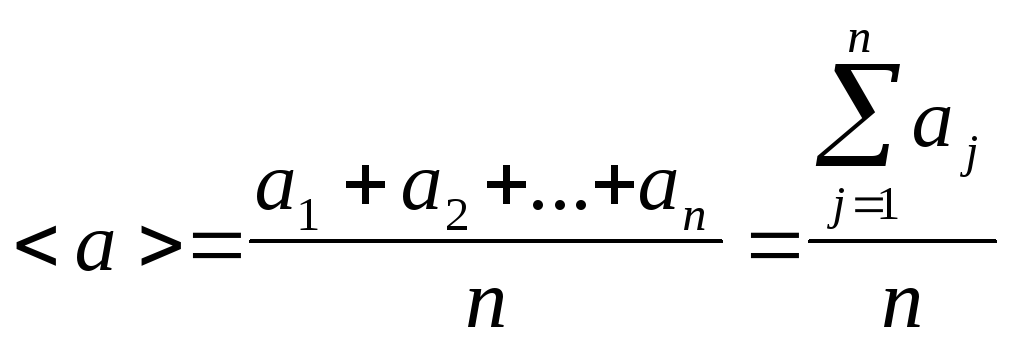^, (13.2)

где - результат j-го измерения случайной величины ;

- число измерений.

Среднее квадратичное значение случайной величины определяется из соотношения:

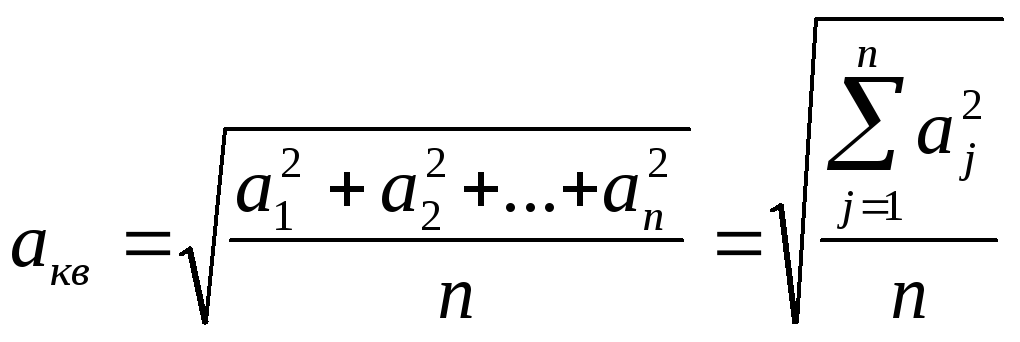^. (13.3)

В теории вероятности доказывается, что знание вида функции распределения для некоторой случайной величины дает возможность определить ее среднее арифметическое и среднее квадратичное значение по формулам:

, (13.4)

. (13.5)