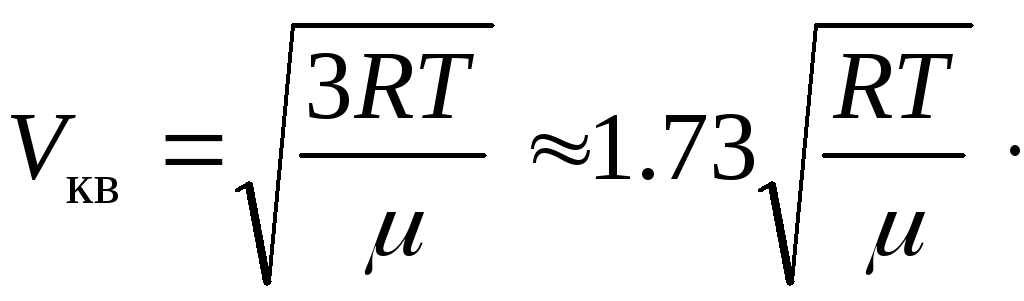- •Глава III. Основы молекулярно-кинетической теории
- •§12. Основные понятия и исходные положения
- •§13. Статистический метод исследования систем. Понятие о случайной величине и функции распределения
- •§14. Идеальный газ
- •§15. Основное уравнение молекулярно - кинетической теории
- •15.1. Вывод основного уравнения молекулярно-кинетической теории
- •15.2. Другие формы записи основного уравнения молекулярно-кинетической теории. Абсолютная температура - мера энергии теплового движения молекул
- •§16. Следствия из основного уравнения молекулярно-кинетической теории
- •§17. Распределение молекул по скоростям и кинетической энергии (распределение Максвелла)
- •§18. Барометрическая формула. Распределение молекул в потенциальном силовом поле (распределение Больцмана)
- •§19. Средняя длина свободного пробега молекул. Понятие о физическом вакууме
- •§20. Закон равномерного распределения энергии по степеням свободы
- •§21. Явления переноса в газах
- •21.1. Диффузия
- •21.2. Внутреннее трение (вязкость)
- •21.3. Теплопроводность
15.2. Другие формы записи основного уравнения молекулярно-кинетической теории. Абсолютная температура - мера энергии теплового движения молекул
Для
практических целей оказывается
целесообразно представить газ
совокупностью одинаковых молекул,
движущихся с так называемой средней
квадратичной скоростью
![]() ,
определяемой из выражения
,
определяемой из выражения
![]() . (15.17)
. (15.17)
В этом случае
![]() (15.18)
(15.18)
и
![]() (15.19)
(15.19)
или
 ,
(15.20)
,
(15.20)
где
![]() - концентрация молекул, а
- концентрация молекул, а
![]() (15.21)
(15.21)
- средняя кинетическая энергия поступательного движения молекулы идеального газа.
Из выражения (15.20) следует, что давление газа пропорционально средней кинетической энергии теплового движения молекул и их концентрации. Действительно, чем выше скорость движения молекул, тем интенсивнее их удары о стенки сосуда, и чем больше концентрация молекул, тем большее их число принимает участие в силовом воздействии на стенки сосуда.
Если записать уравнение Клапейрона-Менделеева (14.1) и основное уравнение в форме (15.19) для одного моля газа, то получим уравнения
![]() (15.22)
(15.22)
и
![]() ,(15.23)
,(15.23)
где
![]() - объем одного моля газа,
- объем одного моля газа,![]() -
постоянная Авогадро. Приравняв правые
части последних двух выражений, получим
-
постоянная Авогадро. Приравняв правые
части последних двух выражений, получим
![]() ,
(15.24)
,
(15.24)
где
- молярная
масса газа,
![]() - постоянная Больцмана.
- постоянная Больцмана.
Подставляя формулу (15.24) в выражение (15.21), получим
![]() . (15.25)
. (15.25)
Следовательно,
средняя кинетическая энергия
поступательного движения молекулы
идеального газа зависит только от его
абсолютной температуры.
Зависимость
![]() от Т
графически
изображена на рис.15.5.
от Т
графически
изображена на рис.15.5.
Таким образом: абсолютная температура является мерой средней кинетической энергии поступательного теплового движения молекул идеального газа.
0
Рис15.5
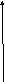

 <wk>
<wk> T
T
Подставляя выражение (15.25) в уравнение (15.26), можно получить еще одну форму записи основного уравнения:
![]() . (15.26)
. (15.26)
§16. Следствия из основного уравнения молекулярно-кинетической теории
Из основного уравнения вытекают важные следствия, являющиеся теоретическим подтверждением опытных газовых законов. Рассмотрим некоторые из них.
Закон Авогадро: в равных объемах разных газов при одинаковых давлениях и температурах содержится одинаковое число молекул.
Действительно, как следует из уравнения (15.26) для числа молекул N в объеме V находим
![]()
то
есть значения N
для
разных газов при одних и тех же
![]() и
и![]() будут
одинаковыми.
будут
одинаковыми.
Закон Дальтона: в состоянии теплового равновесия давление смеси идеальных газов равно сумме парциальных давлений каждого компонента.
Действительно, если в некотором объеме содержится смесь газов, то общая концентрация смеси равна
![]() ,
,
где
![]() концентрация
молекул k-го
газа, и в соответствии с уравнением
(15.26)
концентрация
молекул k-го
газа, и в соответствии с уравнением
(15.26)
![]() ,
,
где
![]() - парциальное давлениеk-го
газа.
- парциальное давлениеk-го
газа.
Законы Бойля-Мариотта, Шарля и Гей-Люссакаполучаются из уравнения (15.26) при постоянстве соответственно температурыT, объемаVи давленияp.
§17. Распределение молекул по скоростям и кинетической энергии (распределение Максвелла)
Закон распределения молекул идеального газа по скоростям, теоретически установленный английским физиком Д.Максвеллом, определяет, какая доля молекул однородного одноатомного идеального газа из общего их числа имеет при данной температуре скорости, заключенные в единичном диапазоне скоростей.
Молекулы газа, участвуя в непрерывном хаотическом движении, сопровождающемся многочисленными столкновениями их друг с другом, в каждый момент времени обладают разными по модулю и направлению скоростями. То, что в газе имеются молекулы как с очень большими, так и с очень малыми скоростями, подтверждается опытами по их измерению. Хотя скорости отдельных молекул газа и непостоянны, в состоянии теплового равновесия газа существует некоторое стационарное распределение молекул по модулям скоростей, то есть доля молекул со скоростями в том или ином диапазоне не изменяется.
Рассматривая
систему N
молекул, каждая из которых движется
между столкновениями независимо и
случайно, Д.Максвелл показал, что
отношение доли
![]() молекул, имеющих модули скорости в малом
диапазоне отV
до
молекул, имеющих модули скорости в малом
диапазоне отV
до
![]() к его величине,
dV
то есть отношение
к его величине,
dV
то есть отношение
![]() может быть выражено зависимостью:
может быть выражено зависимостью:
![]() ,
(17.1)
,
(17.1)
где V - модуль скорости теплового движения молекул, m - масса молекулы, k - постоянная Больцмана, Т -абсолютная температура.
V
Vв
V dV
Рис.17.1




![]() выражает закон распределения
молекул идеального газа по скоростям,
определяя долю молекул, приходящуюся
на единичный диапазон скорости.
выражает закон распределения
молекул идеального газа по скоростям,
определяя долю молекул, приходящуюся
на единичный диапазон скорости.
График функции распределения (17.1) представлен на рис. 17.1
Как
следует из общего определения функции
распределения (§13),
площадь dS
элементарного заштрихованного участка
на этом рисунке численно равна доле
молекул газа, имеющих скорости в
бесконечно малом диапазоне dv,
то есть
![]() ,
а площадьS
под всей кривой распределения равна
единице, что соответствует доле молекул,
имеющих скорости от 0 до
(т.е. все N
молекул).
,
а площадьS
под всей кривой распределения равна
единице, что соответствует доле молекул,
имеющих скорости от 0 до
(т.е. все N
молекул).
Математически это можно сформулировать так:
- для бесконечно малого диапазона скоростей dV
![]() , (17.2)
, (17.2)
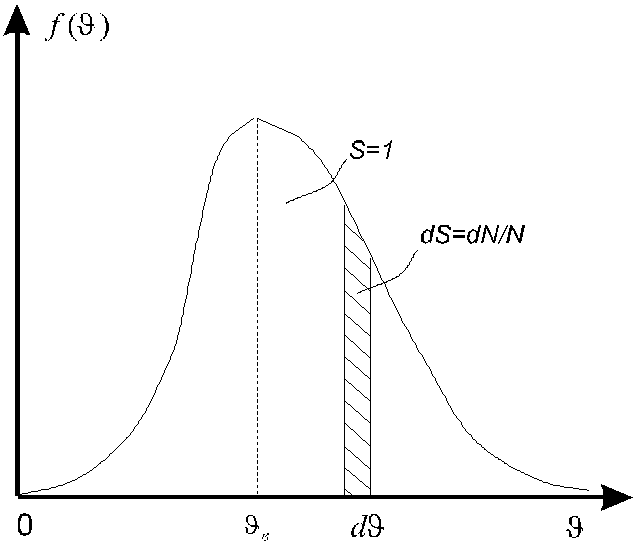
- для конечного диапазона скоростей от V1 до V2
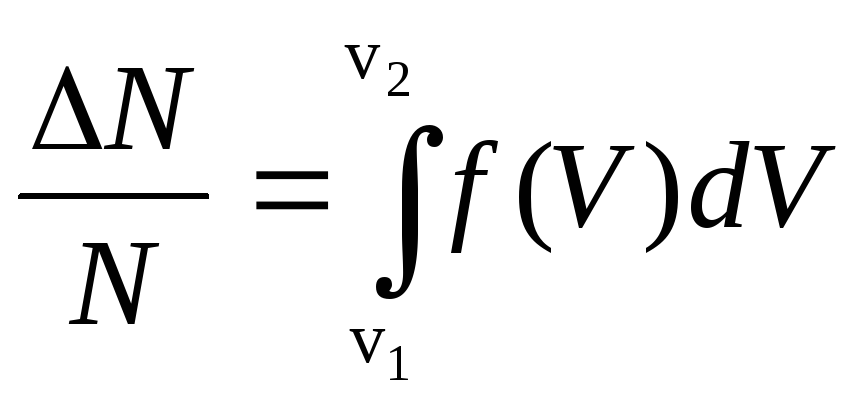 , (17.3)
, (17.3)
- для диапазона скоростей от 0 до
![]() (так
как N=N).
(17.4)
(так
как N=N).
(17.4)
На графике (рис. 17.1) видно, что молекулы распределены по скорости неравномерно: функция f(V) имеет явно выраженный максимум (при V = Vв), а также асимптотически приближается к нулю в области малых и больших скоростей (при V 0 и при V ). Таким образом:
- в газе нет неподвижных молекул, а молекул, имеющих очень большие и очень малые скорости, мало;
- наибольшая доля молекул имеет скорости близкие к наиболее вероятной скорости.
Дифференцируя функцию (17.1) по скорости v и приравнивая полученное выражение к нулю, найдем формулу для наиболее вероятной скорости Vв:
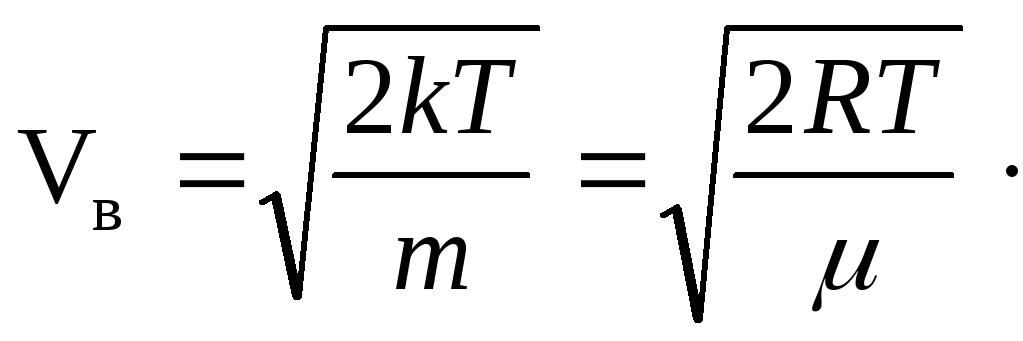 (17.5)
(17.5)
Для примера укажем, что наиболее вероятная скорость молекул кислорода при Т=273К равна 377м/с, при этом распределение молекул по диапазонам скоростей будет следующим (таблица 17.1).
Таблица 17.1
|
Диапазон скоростей, м/с |
Доля молекул % |
|
Менее 100 |
1,4 |
|
100-200 |
8,1 |
|
200-300 |
16,7 |
|
300-400 |
21,5 |
|
400-500 |
20,3 |
|
500-600 |
15,1 |
|
600-700 |
9,2 |
|
более 700 |
7,7 |
Как следует из таблицы 17.1, наибольшее число молекул (21,5%) имеет скорости в том диапазоне, к которому относится наиболее вероятная скорость.
Рис.17.2
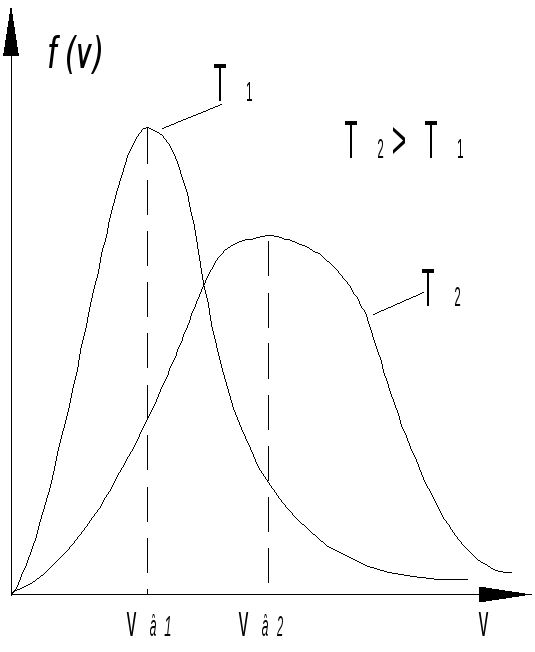
Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями, уменьшается, а обладающих большими скоростями - увеличивается.
Исходя
из распределения молекул по скоростям
(17.1), можно найти распределение молекул
по значениям кинетической энергии Wk
поступательного
движения, равной
![]() .
Произведя в (17.1) подстановку
.
Произведя в (17.1) подстановку
![]()
и
![]() ,
,
получим распределение
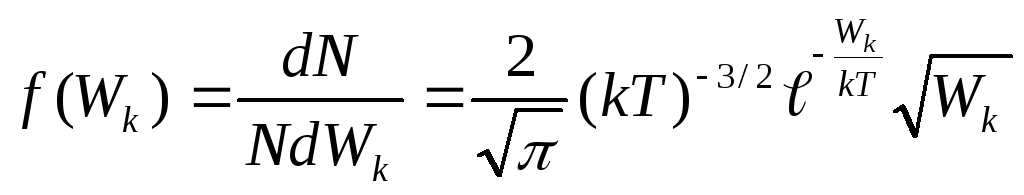 .
(17.6)
.
(17.6)
Закон распределения молекул по скоростям позволяет определить по формуле (13.4) и среднюю арифметическую скорость <V> поступательного движения молекул идеального газа. Расчеты приводят к следующей формуле:
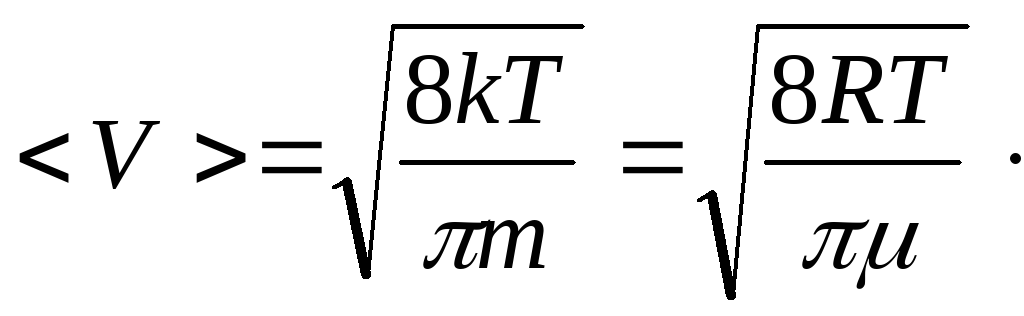 (17.7)
(17.7)
Таким образом, состояние идеального газа характеризуется скоростями:
- наиболее вероятной скоростью, к которой близки скорости большинства молекул:
![]() ;
;
- средней арифметической скоростью, которая определяет среднее значение модуля импульса молекулы:
![]() ;
;
- средней квадратичной скоростью, которая определяет среднее значение энергии поступательного хаотического движения молекулы: