
- •Глава 12. Функциональные ряды
- •12.1. Сходимость функциональных последовательностей и рядов
- •11.2. Функциональные свойства предельной функции и суммы ряда
- •11.3. Степенные ряды
- •11.4. Ряд Тейлора
- •11.5. Тригонометрические ряды Фурье
- •11.6. Свойства коэффициентов Фурье
- •11.7. Сходимость ряда Фурье
- •11.8. Тригонометрические ряды в комплексной форме
- •11.9. Интеграл Фурье
- •11.10. Контрольные вопросы
- •11.11. Задачи для самостоятельного решения.
11.6. Свойства коэффициентов Фурье
Коэффициенты ряда Фурье обладают рядом важных свойств.
1.
Если
 имеет период
имеет период (например, рис. 11.1), то коэффициенты ряда
Фурье для нее вычисляются по следующим
формулам
(например, рис. 11.1), то коэффициенты ряда
Фурье для нее вычисляются по следующим
формулам

 ,
,
 ,
, .
.
Известны свойства периодических функций
а)
 ;
;
б)
 ;
;
в)
 .
.
Тогда доказываемые
формулы получаются, если в них положить
 ,
, .<
.<
2.
Если
 четная функция, то
четная функция, то для
для .
.
Если
 нечетная функция, то
нечетная функция, то ,
, для
для .
.
По определению: четная функция
удовлетворяет условию
 ,
а нечетная
,
а нечетная .
Известно, что:
.
Известно, что:
а)
если
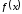 ,
, четные функции, то
четные функции, то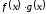 – четная;
– четная;
б)
если
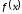 нечетная, а
нечетная, а четная, то
четная, то – нечетная;
– нечетная;
в)
если
 и
и нечетная, то
нечетная, то – четная.
– четная.
Тогда,
если
 – четная, то
– четная, то – нечетная, т.к.
– нечетная, т.к. нечетная.
нечетная.
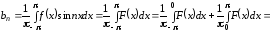

 .
.
Таким образом,
 .
Аналогично доказывается, что если
.
Аналогично доказывается, что если нечетная, то
нечетная, то .<
.<
Из этого свойства
следует, что тригонометрический ряд
Фурье для четных функций
 имеет вид
имеет вид
 ,
,
где
 ,
, ,
,
Для нечетных функций тригонометрический ряд Фурье соответственно имеет вид
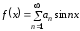 ,
,
где
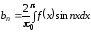 ,
,
Сделанные выводы сохраняются для тригонометрических рядов по системе общего вида. Для четной функции:
 ,
,
где
 ,
, .
.
Для нечетной функции:
 ,
,
где
 .
.
3.
Лемма Римана.
Если
 кусочно-непрерывная функция на
кусочно-непрерывная функция на ,
то
,
то ,
, .
.
Пусть
 ,
, ,
…,
,
…, точки разрыва функции
точки разрыва функции .
Для доказательства достаточно показать,
что интегралы от функции
.
Для доказательства достаточно показать,
что интегралы от функции и
и по каждому из отрезков
по каждому из отрезков ,
, ,
…,
,
…, стремятся к нулю при
стремятся к нулю при .
Пусть
.
Пусть один из таких отрезков,
один из таких отрезков, непрерывна на
непрерывна на .
Покажем, что
.
Покажем, что .
.
Функция
 непрерывна на
непрерывна на ,
следовательно, она ограничена
,
следовательно, она ограничена
 для
для (24)
(24)
и
по теореме Кантора равномерно непрерывна.
Следовательно, для

 такое, что для
такое, что для выполняется
выполняется ,
тогда
,
тогда
 для
для
 .
(25)
.
(25)
Зададим
 и выберем на
и выберем на с шагом
с шагом разбиение
разбиение так, чтобы
так, чтобы ,
, и
и .
.
Произведем оценку интеграла:

 .
.
Так как
 ,
то из (24) и (25) имеем
,
то из (24) и (25) имеем
 ,
,
при
 .
.
Откуда
следует, что при
 имеем
имеем
 ,
т.е.
,
т.е.
 .<
.<
Тогда, очевидно,
что для кусочно-непрерывной на
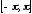 функции
функции
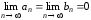 .
.
Последнее следует из формул (23).

Пример 25. Разложить в ряд Фурье двумя способами функцию, представленную на рис. 11.2 по косинусам и по синусам.
Решение.
а) Разложение
 в ряд по косинусам. Продолжим
в ряд по косинусам. Продолжим ,
как показано на рис. 11.3, получим четную
функцию
,
как показано на рис. 11.3, получим четную
функцию ,
определенную на
,
определенную на и совпадающую с
и совпадающую с на
на .
.
Вычислим коэффициенты
ряда Фурье, учитывая, что

 .
.



 .
.
Разложение будет иметь вид

 .
.
б) Разложение
 в ряд по синусам. Продолжим
в ряд по синусам. Продолжим ,
как показано на рис. 11.4, получим функцию
,
как показано на рис. 11.4, получим функцию ,
определенную на
,
определенную на и совпадающую с
и совпадающую с на
на .
.

Вычислим коэффициенты
ряда Фурье. Так как получившаяся функция
 нечетная, то
нечетная, то

 .
.
Получаем выражение
для ряда Фурье заданной функции

 .
.
11.7. Сходимость ряда Фурье
Рассмотрим вопрос
о сходимости ряда Фурье. Вначале заметим,
что если ряд Фурье
 сходится на отрезке
сходится на отрезке к функции
к функции ,
то в силу периодичности его членов он
сходится на всей числовой прямой к
периодической функции. Эта функция
является периодическим продолжением
с периодом
,
то в силу периодичности его членов он
сходится на всей числовой прямой к
периодической функции. Эта функция
является периодическим продолжением
с периодом функции
функции .
Поэтому будем считать, что на числовой
прямой задана периодическая с периодом
.
Поэтому будем считать, что на числовой
прямой задана периодическая с периодом функция
функция ,
интегрируемая на
,
интегрируемая на и для нее написан ряд Фурье с коэффициентами,
определенными по формулам (23).
и для нее написан ряд Фурье с коэффициентами,
определенными по формулам (23).
Теорема 15. (Дирихле) Пусть выполняются условия:
1)
 периодическая с периодом
периодическая с периодом функция;
функция;
2)
 кусочно-непрерывная на
кусочно-непрерывная на ;
;
3)
 имеет в каждой точке
имеет в каждой точке правую и левую производные.
правую и левую производные.
Тогда
ряд Фурье функции
 сходится всюду, причем его сумма в точках
непрерывности функции равна
сходится всюду, причем его сумма в точках
непрерывности функции равна ,
а в точках разрыва равна
,
а в точках разрыва равна .
.
Вначале получим интегральное представление
для частичной суммы
 .
.

 .
.
Воспользуемся формулой
 (26)
(26)
и получим
 .
.
Производя замену
 ,
получаем
,
получаем
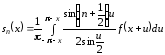 .
.
Так как под
интегралом стоит периодическая с
периодом
 функция, то интеграл по любому отрезку
функция, то интеграл по любому отрезку имеет одно и тоже значение
имеет одно и тоже значение

 .
.
Заменяя в первом
интеграле
 ,
получаем
,
получаем

 .
(27)
.
(27)
Из (26) следует, что
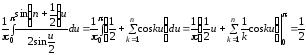 .
.
Тогда в силу (27) имеем



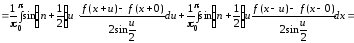
 .
(27)
.
(27)
Функции
 и
и кусочно-непрерывны на
кусочно-непрерывны на ,
так как имеют разрывы первого ряда в
тех же точках, что и функции
,
так как имеют разрывы первого ряда в
тех же точках, что и функции и
и соответственно. При
соответственно. При
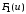 и
и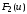 можно считать непрерывными, так как в
силу условий теоремы существуют пределы
можно считать непрерывными, так как в
силу условий теоремы существуют пределы
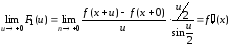 –правая производная.
–правая производная.
 –левая производная.
–левая производная.
Перейдем в (27) к
пределу при
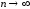 .
В силу Леммы Римана при
.
В силу Леммы Римана при оба интеграла равны 0. Следовательно,
для
оба интеграла равны 0. Следовательно,
для выполняется
выполняется
 .
.
В частности, если
 – точка непрерывности функции
– точка непрерывности функции ,
то
,
то и
и .<
.<
Теперь рассмотрим достаточные условия равномерной сходимости тригонометрического ряда Фурье.
Определение 7.
Говорят, что функция
 имеет на отрезке
имеет на отрезке кусочно-непрерывную производную, если
кусочно-непрерывную производную, если существует и непрерывна на отрезке
существует и непрерывна на отрезке ,
за исключением может быть конечного
числа точек, в каждой из которых функция
,
за исключением может быть конечного
числа точек, в каждой из которых функция имеет пределы слева и справа.
имеет пределы слева и справа.
Теорема
16. Пусть
 непрерывная периодическая (с периодом
непрерывная периодическая (с периодом )
функция, имеющая на отрезке
)
функция, имеющая на отрезке кусочно-непрерывную производную. Тогда
ряд Фурье функции
кусочно-непрерывную производную. Тогда
ряд Фурье функции сходится абсолютно и равномерно на всей
числовой прямой.
сходится абсолютно и равномерно на всей
числовой прямой.
По условиям теоремы
 имеет кусочно-непрерывную производную,
тогда она в каждой точке имеет левую и
правую производные, и, таким образом,
имеет кусочно-непрерывную производную,
тогда она в каждой точке имеет левую и
правую производные, и, таким образом, удовлетворяет всем условиям теоремы 1
и поэтому ряд Фурье сходится всюду к
удовлетворяет всем условиям теоремы 1
и поэтому ряд Фурье сходится всюду к .
Докажем, что ряд сходится абсолютно и
равномерно.
.
Докажем, что ряд сходится абсолютно и
равномерно.
Пусть
 и
и коэффициенты Фурье функции
коэффициенты Фурье функции .
Тогда
.
Тогда

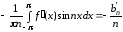 .
.
Аналогично
получаем, что
 .
.
Рассмотрим числовой ряд
 .
.
Этот
ряд сходится, так как
 ,
, ,
а ряды
,
а ряды ;
; ,
, – сходятся. Сходимость первых двух
рядов следует из неравенства Бесселя
– сходятся. Сходимость первых двух
рядов следует из неравенства Бесселя
 .
.
Из сходимости ряда
 в силу признака Вейерштрасса следует
абсолютная и равномерная сходимость
ряда Фурье на всей числовой прямой.<
в силу признака Вейерштрасса следует
абсолютная и равномерная сходимость
ряда Фурье на всей числовой прямой.<
Замечание. Доказанная теорема естественно переносится на тригонометрические ряды Фурье периодических функций с произвольным периодом.
