
- •Глава 8. Неявные функции. Дифференцируемые Отображения
- •8.1. Неявные функции заданные одним уравнением
- •8.2. Векторные отображения
- •В силу (13) это будет означать, что
- •Предел отображения обозначается:
- •8.3. Неявные функции n-переменных. Обратные отображения
- •8.4. Условный экстремум
- •8.5. Поверхности в трехмерном евклидовом пространстве
- •8.6. Контрольные вопросы
- •8.7. Примеры решения задач
- •8.8. Задачи для самостоятельного решения
Глава 8. Неявные функции. Дифференцируемые Отображения
8.1. Неявные функции заданные одним уравнением
Пусть
функция двух переменных
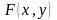 определена на некотором множестве
определена на некотором множестве
 плоскости
плоскости
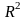 переменных
переменных
 ,
и существует функция
,
и существует функция
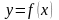 одного переменного
одного переменного
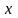 ,
определенная на некотором множестве
,
определенная на некотором множестве
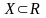 ,
причем имеет место включение
,
причем имеет место включение
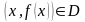 ,
и выполняется равенство
,
и выполняется равенство
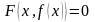 .
В этом случае функция
.
В этом случае функция
 ,
определяемая уравнением
,
определяемая уравнением
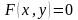 ,
называется неявно
заданной функцией.
,
называется неявно
заданной функцией.
Если
в трехмерном пространстве
 задан цилиндр (рис.8.1)
задан цилиндр (рис.8.1)


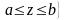
и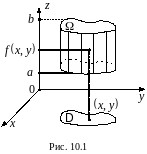 в этом цилиндре определена функция
в этом цилиндре определена функция
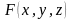 .
Тогда, если существует такая функция
.
Тогда, если существует такая функция
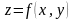 двух переменных
,
определенная на множестве
двух переменных
,
определенная на множестве
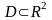 такая, что имеет место включение
такая, что имеет место включение
 ,
и при этом выполняется равенство
,
и при этом выполняется равенство
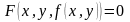 ,
то говорят, что функция
– неявная
функция,
заданная уравнением
,
то говорят, что функция
– неявная
функция,
заданная уравнением
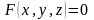 .
.
Пример
1. Уравнение
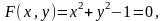 задает неявно бесконечное множество
функций, определенных на
задает неявно бесконечное множество
функций, определенных на
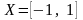 (рис.8.2).
(рис.8.2).
Пример
2. Рассмотрим
функцию
![]() .
Пусть
.
Пусть
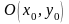 – некоторая окрестность точки
– некоторая окрестность точки
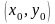 ,
и координаты точки
удовлетворяют уравнению
,
и координаты точки
удовлетворяют уравнению
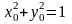 ,
,
![]() .
Тогда существует единственная неявная
функция, такая, что ее график содержится
в
(рис. 8.3).
.
Тогда существует единственная неявная
функция, такая, что ее график содержится
в
(рис. 8.3).

П ример
3. Уравнение
ример
3. Уравнение
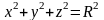
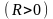 задает бесконечное множество неявных
функций, определенных при
задает бесконечное множество неявных
функций, определенных при
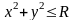 ,
т.е.
– круг радиусом
,
т.е.
– круг радиусом
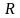 .
В самом деле, формула
.
В самом деле, формула
 ,
в которой для каждой из точек
,
в которой для каждой из точек
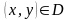 знак перед корнем выбирается произвольно,
определяет неявную функцию. Заметим,
что функции
знак перед корнем выбирается произвольно,
определяет неявную функцию. Заметим,
что функции
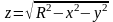 и
и
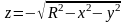 заданны в
заданны в
 ,
непрерывны в
и дифференцируемы в
,
непрерывны в
и дифференцируемы в
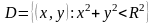 .
.
Все
рассуждения в дальнейшем, даются для
уравнения
![]() .
.
Теорема
8.1. (Существование
неявной функции). Пусть функция
определена в цилиндре
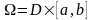 ,
непрерывна по
,
непрерывна по
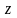 при фиксированных
и
при фиксированных
и
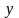 ,
и выполняется неравенство
,
и выполняется неравенство
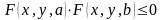 .
Тогда существует, по крайней мере, одна
неявная функция
,
заданная уравнением
.
Тогда существует, по крайней мере, одна
неявная функция
,
заданная уравнением
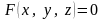 ,
(1)
,
(1)
определенная на множестве .
Пусть
произвольная точка принадлежащая
.
По условию теоремы функции
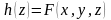 ,
при фиксированных значениях
,
при фиксированных значениях
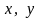 ,
непрерывна на
,
непрерывна на
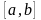 .
В силу теоремы Коши (из свойств функций
непрерывных на отрезке) функция
.
В силу теоремы Коши (из свойств функций
непрерывных на отрезке) функция
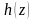 принимает любое промежуточное значение
между
принимает любое промежуточное значение
между
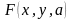 и
и
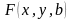 .
Так как
и
имеют различные знаки, то
принимает и нулевое значение, т.е.
существует хотя бы одна точка
.
Так как
и
имеют различные знаки, то
принимает и нулевое значение, т.е.
существует хотя бы одна точка
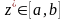 ,
в которой
,
в которой
 .
Положим,
.
Положим,
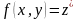 .
Таким образом построена неявная функция
,
определенная на
.
.
Таким образом построена неявная функция
,
определенная на
.
Теорема
8.2.
(Единственность). Пусть
определена в цилиндре
 ,
при фиксированных
и
из области
и строго монотонна по переменной
.
Тогда не может существовать более одной
неявной функции
,
определенной на
.
,
при фиксированных
и
из области
и строго монотонна по переменной
.
Тогда не может существовать более одной
неявной функции
,
определенной на
.
Предположим, что существуют две
различные функции
и
 ,
заданные уравнением (2). Тогда найдется
такая хотя бы одна точка
,
заданные уравнением (2). Тогда найдется
такая хотя бы одна точка
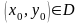 ,
что
,
что
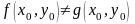 .
Однако из сделанного предположения,
имеем
.
Однако из сделанного предположения,
имеем
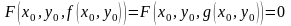 .
Последнее невозможно, так как
.
Последнее невозможно, так как
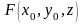 строго монотонна по
,
т.е.
строго монотонна по
,
т.е.
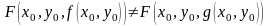 .
Получаем противоречие с условием.
Следовательно, функция
единственна.
.
Получаем противоречие с условием.
Следовательно, функция
единственна.
Следствие.
Пусть функция
непрерывна по
в цилиндре
,
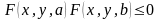 для точки
для точки
![]() .
Пусть также
дифференцируема по
в открытом цилиндре
.
Пусть также
дифференцируема по
в открытом цилиндре
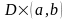 ,
причем
,
причем
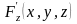 сохраняет знак в этом цилиндре. Тогда
уравнение (1) задает единственную неявную
функцию, определенную на
.
сохраняет знак в этом цилиндре. Тогда
уравнение (1) задает единственную неявную
функцию, определенную на
.
По
теореме 8.1 существует, по крайней мере,
одна неявная функция
![]() .
Так как
сохраняет знак в открытом цилиндре, то
строго монотонна по
на
.
Следовательно, по теореме 8.2 неявная
функция
определена единственным образом.
.
Так как
сохраняет знак в открытом цилиндре, то
строго монотонна по
на
.
Следовательно, по теореме 8.2 неявная
функция
определена единственным образом.
Теорема
8.3 (Непрерывность
неявной функции). Пусть функция
непрерывна в цилиндре
;
для любой точки
выполняется условие
;
функция
дифференцируема в открытом цилиндре
 и
и
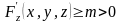 в
.
Тогда уравнение (1) определяет единственным
образом неявную функцию
,
которая непрерывна на множестве
.
в
.
Тогда уравнение (1) определяет единственным
образом неявную функцию
,
которая непрерывна на множестве
.
Существование и
единственность неявной функции
определяются следствием и теоремой
8.2. Для доказательства непрерывности
функции
рассмотрим разность
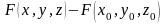 .
Применяя формулу конечных приращений
Лагранжа, получаем
.
Применяя формулу конечных приращений
Лагранжа, получаем
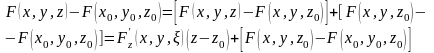 (2)
(2)
Положим
,
тогда
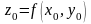 .
Следовательно,
.
Следовательно,
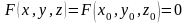 .
Используя условие
,
из (2) получаем
.
Используя условие
,
из (2) получаем
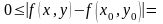
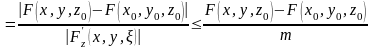 .
(3)
.
(3)
Переходя
в неравенствах (3) к пределу при
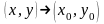 в силу непрерывности функции
в силу непрерывности функции
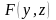 ,
имеем
,
имеем
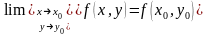 .
.
Следовательно, неявно заданная функция непрерывна в любой точке .
Теорема
8.4
(Дифференцирование неявной функции).
Пусть функция
непрерывна в цилиндре
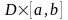 ,
где
открытое множество; выполняется условие
,
где
открытое множество; выполняется условие
 ;
функция
дифференцируема в открытом цилиндре
и
.
Тогда уравнение (1) определяет единственным
образом неявную функцию
,
которая дифференцируема на
и справедливы равенства
;
функция
дифференцируема в открытом цилиндре
и
.
Тогда уравнение (1) определяет единственным
образом неявную функцию
,
которая дифференцируема на
и справедливы равенства
 ,
,
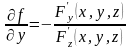 , (4)
, (4)
где .
Существование
и единственность неявной функции
вытекает из теорем 8.1 и 8.2. При этом
непрерывна на
по теореме 8.3. Так как функция трех
переменных дифференцируема на открытом
множестве
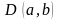 ,
то
,
то
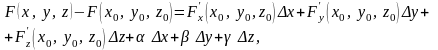 (5)
(5)
где
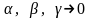 при
при
 .
.
Положим
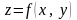 ,
тогда для точки
,
тогда для точки
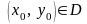 имеем
имеем
 и
и
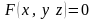 ,
,
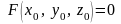 . (6)
. (6)
Из (5) и (6) получим
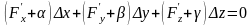 .
.
Так
как
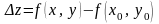 ,
то
,
то
 . (7)
. (7)
Поскольку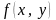 непрерывна, то
непрерывна, то
 при
при
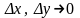 .
Следовательно, так как
.
Следовательно, так как
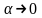 ,
,
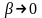 и
и
 при
при
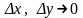 ,
то по теореме о пределе отношения двух
функций получаем
,
то по теореме о пределе отношения двух
функций получаем
 ,
,
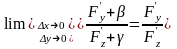 .
.
Отсюда следует, что
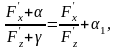
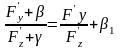 , (8)
, (8)
где
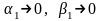 при
.
при
.
Из (7) и (8) следует
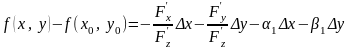 .
.
Таким
образом,
дифференцируемая функция в произвольной
точке
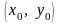 и
и
 ,
,
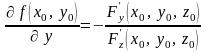 ,
,
где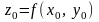 .
.
Теорема
8.5. Пусть
функция
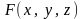 дифференцируема в
дифференцируема в
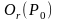 ,
где
,
где
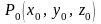 – точка области определения функции,
и
– точка области определения функции,
и
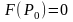 ;
частная производная
;
частная производная
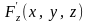 непрерывна в окрестности
и
непрерывна в окрестности
и
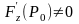 .
Тогда существует такой открытый цилиндр
.
Тогда существует такой открытый цилиндр
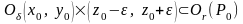 ,
что уравнение
,
что уравнение
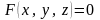 задает единственным образом неявную
функцию
,
определенную в окрестности
задает единственным образом неявную
функцию
,
определенную в окрестности
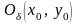 .
При этом функция
дифференцируема и ее производные
вычисляются по формулам (4).
.
При этом функция
дифференцируема и ее производные
вычисляются по формулам (4).
Пусть
для определенности
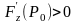 .
Так как
непрерывна в окрестности
,
то существует такой замкнутый шар (рис.
8.4)
.
Так как
непрерывна в окрестности
,
то существует такой замкнутый шар (рис.
8.4)
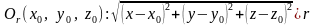 ,
,
что
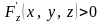 при
при
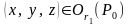 .
.
 В
силу теоремы Вейерштрасса непрерывная
функция
В
силу теоремы Вейерштрасса непрерывная
функция
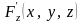 достигает своего наименьшего значения
на шаре
достигает своего наименьшего значения
на шаре
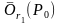 .
Поэтому
.
Поэтому
 .
Выберем
.
Выберем
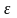 и
и
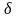 столь малыми, чтобы цилиндр удовлетворял
условию:
столь малыми, чтобы цилиндр удовлетворял
условию:
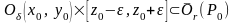 .
.
Тогда
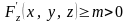 при
при
 .
.
Функция
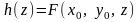 монотонно возрастает на
монотонно возрастает на
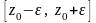 ,
,
так
как
 на этом отрезке. Поскольку
на этом отрезке. Поскольку
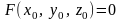 ,
то имеют место неравенства:
,
то имеют место неравенства:
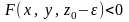
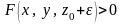 .
.
В
силу теоремы 8.4 уравнение (2) задает
единственным образом неявную функцию
,
определенную в окрестности
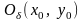 ,
причем эта функция дифференцируемая и
ее производные вычисляются по формуле
(4).
,
причем эта функция дифференцируемая и
ее производные вычисляются по формуле
(4).
Замечание 1. Аналогичные теоремы имеют место для функционального уравнения
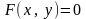 .
(9)
.
(9)
Областью
здесь является интервал
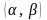 ,
т.е.
,
т.е.
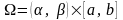 – прямоугольник на плоскости
– прямоугольник на плоскости
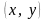 (рис. 8.5). Здесь неявная функция
и ее производные вычисляются по формуле
(рис. 8.5). Здесь неявная функция
и ее производные вычисляются по формуле
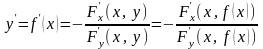 .
(10)
.
(10)
Замечание
2. Важным в
теореме 8.4, а следовательно в формуле
(4) и в формуле (10) является отличие от
нуля производной стоящей в знаменателе.
Например, если
 ,
то уравнение (9) может иметь не единственное
решение относительно функции в точке
,
то уравнение (9) может иметь не единственное
решение относительно функции в точке
 ,
а может не иметь ни одного, решения.
,
а может не иметь ни одного, решения.
Д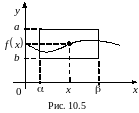 ля
уравнения
ля
уравнения
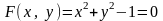 получаем
получаем
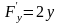 ,
,
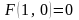 ,
а
,
а
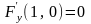 .
Очевидно, что в окрестности точки (1, 0)
при
.
Очевидно, что в окрестности точки (1, 0)
при
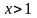 ,
уравнение не имеет решения относительно
,
т.е. неявная функция не существует. А
при
,
уравнение не имеет решения относительно
,
т.е. неявная функция не существует. А
при
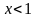 уравнение
уравнение
 имеет два решения
имеет два решения
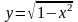 и
и
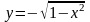 ,
т.е. задает две неявные функции.
,
т.е. задает две неявные функции.
Вместе
с тем, надо отметить, что условия
 (или
(или
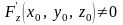 )
являются лишь достаточными. Если они
не выполняются, то неявная функция может
существовать. Например, для уравнения
)
являются лишь достаточными. Если они
не выполняются, то неявная функция может
существовать. Например, для уравнения
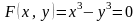 в точке (0, 0) они не выполняется, однако,
в окрестности точки (0, 0) существует
единичная неявная функция
в точке (0, 0) они не выполняется, однако,
в окрестности точки (0, 0) существует
единичная неявная функция
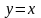 .
.
Пример 4. Найти частные производные функции, заданной уравнением:

