11.8. Тригонометрические ряды в комплексной форме

Рассмотрим ряд Фурье

(28)

функции , заданной на отрезке. Введем комплекснозначную функцию действительного переменного:

, где .

Она обладает всеми свойствами показательной функции:

;

;

;

.

Из определения следуют формулы, которые называются формулами Эйлера

, .

Тогда

где ,,,, т.е.

(29)

Теперь, если воспользоваться формулами для коэффициентов Фурье, будем иметь

,

,

,

Эти формулы можно объединить в одну:

,(30)

Ряд коэффициенты которого определяются по формулам (30) называетсярядом Фурье в комплексной форме функции . Коэффициенты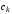называютсякоэффициентами Фурье.

Если функция задана на отрезке, то ряд Фурье в комплексной форме имеет вид, где,

Пример 26. Построить ряд Фурье для функции ,.

Решение. Определим коэффициенты ряда Фурье

,

, .

Получаем ряд Фурье:

при .

В точках сумма этого ряда равна 0.

11.9. Интеграл Фурье

Пусть функция задана на всей числовой прямойи абсолютна интегрируема на ней. Составим для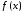интеграл, соответствующий в определенном смысле ряду Фурье, в котором суммирование по индексузаменено интегрированием по параметру:

, (31)

где ,. (32)

Интеграл (31) аналогичен ряду Фурье периодической функции, только суммирование заменено интегрированием. Подставим (32) в (31), получим

.

Определение 8. Интеграл

(33)

называется интегралом Фурье функции .

Подобно тому, как при некоторых условиях периодическая функция раскладывается в ряд Фурье, так и при некоторых условиях , определенная на всей числовой представляется своим интегралом Фурье.

Теорема 17. Пусть:

1) 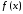кусочно-непрерывная на любом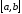числовой прямой;

2) имеют всюду правую и левую производные, т.е. идля;

3) интеграл сходится.

Тогда при любом имеет место равенство

. (34)

(Без доказательства.)

Вспомним понятие главного значения несобственного интеграла на действительной оси. Если интегрируема в собственном или несобственном смысле на любом отрезке числовой прямой(т.е. локально интегрируема), тогда

v.p., (35)

где v.p. сокращение от value principle.

Отличие интеграла, стоящего справа, от интеграла слева в равенстве (35), состоит в том, что является пределом интеграловпри произвольном стремлении,, а интеграл (35) предел тех же интегралов, но прии. Если существует несобственный интеграл, то существует и интеграл в смыслеv.p., но не наоборот.

Например, не существует, аv.p. существует и равен нулю. Если – нечетная, то v.p. .

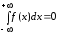Пусть функция непрерывна и абсолютно интегрируема на всей числовой прямой, и имеет в односторонние производные, тогда по теореме 15

.

Отсюда, в силу четности косинуса, следует, что

.

Рассмотрим функцию

Она непрерывна и абсолютно интегрируема по признаку Вейерштрасса, так как , а– абсолютно интегрируема. В силу нечетности синусатакже нечетная, поэтому

v.p. .

Тогда

.

Перепишем полученное равенство

.

Определение 9. Отображение F, ставящее в соответствие функции функцию(или), определяемое формулой

называется преобразованием Фурье.

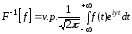Отображение , ставящее в соответствие функции, функцию, определяемую формулойназываетсяобратным преобразованием Фурье. Из формулы ясно, что .