Дополнительные примеры поиска производных

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) .

Замечание 4. Не забывайте, что тригонометрические функции нелинейны. Например, ,, , и т.д. Записииравноправны. Если имеется в виду функция, пишут.

Примеры поиска производных для функций тройной вложенности

1) ;

2)

;

3)

;

4)

;

5)

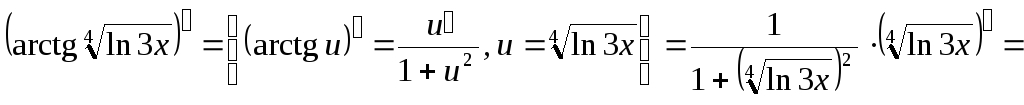
(сократили);

6)

.

ОД11. Слева даны функции , справа – их производные, причём в решении каждого примераесть ошибка, как правило, небольшая. Закрыв правый столбец, найдите (или хотя бы предложите) собственное решение. Сравните его с табличным, а затем – с правильным на с. 95 – 96.

Для примеров, где и ваш вариант оказался ошибочен (а лучше – ещё раз для всех примеров), через некоторое время повторите решение и сравните с правильным – пока не избавитесь от ошибок.

№		с ошибкой
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

ОД12. Найдите производные функций

1) а) ; б); в); г);

2) а) ; б); в); г);

3) а) ; б);

в) ; г);

4) а) ; б);

в) ; г);

5) а) ; б); в);

г) ; д); е);

6) а) ; б); в);

г) ; д); е).

ОД13. Найдите производные функций :

1) ;	2) ;	3) ;
4) ;	5) ;	6) ;
7) ;	8) ;	9) ;
10) ;	11) ;	12) ;
13) ;	14) ;	15) ;
16) ;	17) ;	18) ;
19) ;	20) ;	21) ;
22) ;	23) ;	24) ;
25) ;	26) ;	27) ;
28) ;	29) ;	30) .

§ 7. Логарифмическое дифференцирование

Логарифмическое дифференцирование обычно применяют, чтобы найти производные от степенно-показательных функций или от произведенийи дробей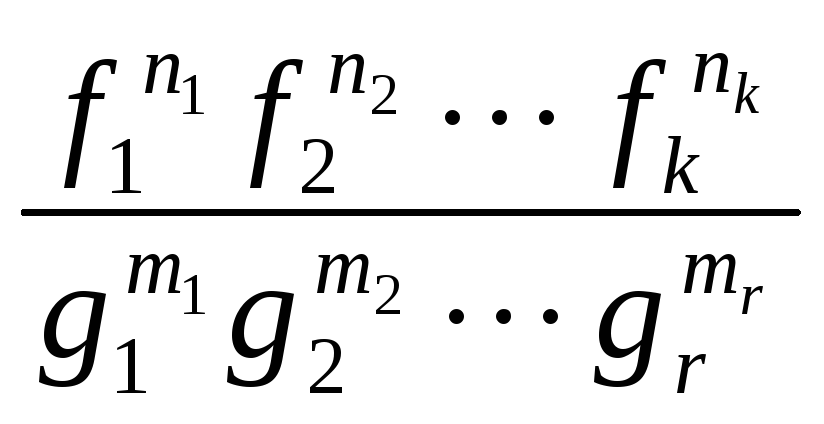, где– действительные числа.

В этих случаях можно найти логарифм функции, упростить его по основным свойствам логарифмов, продифференцировать то, что получилось, и умножить на первоначальную функцию.

Правило дифференцирования следует из формулы.

Пример 1. Применяя свойство, находим

,

тогда

,

т.е. . Поэтому

,

или, после раскрытия скобок, .

Пример 2. Здесь, тогда

,

поэтому .

Пример 3. Найдём производную функции .

Логарифмируем:

,

выносим степень:

,

дифференцируем:

.

Тогда

.

Пример 4.

Можно раскрыть скобки, привести подобные слагаемые и продифференцировать частное, но лучше найти

и затем .

Полученную сумму умножим на исходную функцию. Раскрывать скобки нет смысла – наоборот, в таких задачах желательно выносить общий множитель. Итак,

.

Пример 5.

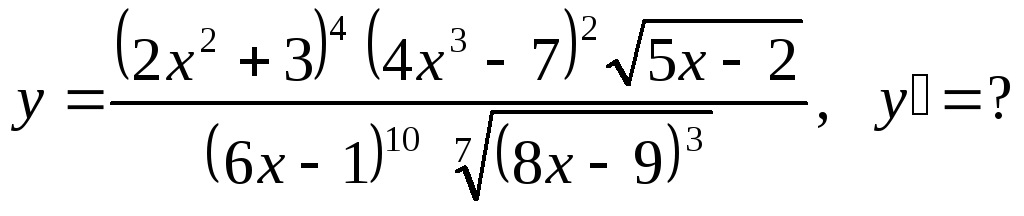
Раскрыть скобки невозможно из-за корней, и непосредственное дифференцирование весьма громоздко. Поэтому ищем

,

затем по свойству логарифма выносим степени:

,

и тогда

.

Окончательно

.

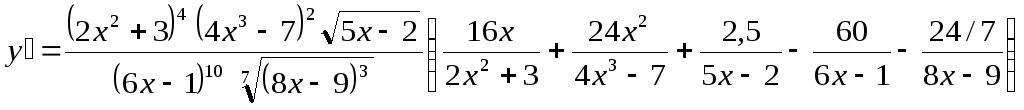ЛД1. Найдите производные функций

1) ;

2) ;

3) ;

4) ;

5) .

ЛД2. Найдите производные функций при помощи логарифмического дифференцирования. Укажите, в каких точках производная не определена:

1) ;

2) ;

3) .

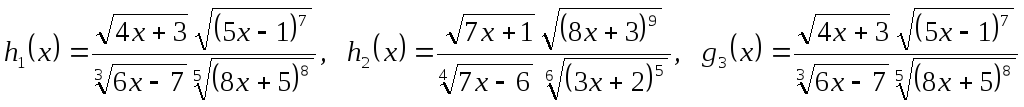ЛД3. Найдите производные при помощи логарифмирования:

1) а) ; б);

2) а) ; б);

3) а) ; б).

Пример 6. Пусть , тогда

,

соответственно

,

и тогда

.