- •Глава 1. Матрицы и определители
- •§1. Матрицы и их виды
- •§2. Определители 2, 3 и n-го порядка
- •§3. Действия над матрицами
- •2 Способ (с помощью элементарных преобразований):
- •§5. Ранг матрицы.
- •§6.Формулы Крамера
- •§7. Метод Гаусса
- •§8. Матричный метод решения систем линейных уравнений
- •§10.1 Линейная зависимость векторов
- •§10.2 Базис и размерность линейного векторного пространства
- •§11.1 Скалярное произведение двух векторов в r2 и r3
- •§11.2 Скалярное произведение двух n-мерных векторов. Евклидово пространство
- •§12. Линейные операторы
- •Алгебра линейных операторов
- •§13. Собственные векторы и собственные числа линейного оператора
- •Часть 2. Элементы аналитической геометрии
- •§1. Понятие уравнения линии. Составление уравнения линии
- •§2.Уравнение прямой с угловым коэффициентом
- •§8Расстояние от точки до прямой
- •§14Гипербола
- •§15Парабола
- •§16Приведение квадратичных форм к каноническому виду
- •§17Приведение общего уравнения кривой 2-го порядка к каноническому виду
- •§18.Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •§19Общее уравнение плоскости
- •§20 Взаимное расположение двух плоскостей
- •§21 Нахождение координат любой точки, принадлежащей данной плоскости.
- •22Прямая в пространстве
- •§23Угол между прямыми в пространстве
- •Условия параллельности и перпендикулярности
§10.1 Линейная зависимость векторов
Определение
1.
Вектор
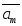 называетсялинейной
комбинацией
векторов
называетсялинейной
комбинацией
векторов
 векторного пространства
векторного пространства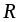 ,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
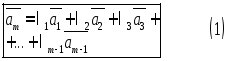
Определение
2.
Векторы
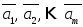 векторного пространства
векторного пространства называютсялинейно
зависимыми,
если существуют такие числа
называютсялинейно
зависимыми,
если существуют такие числа
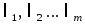 ,
не равные одновременно нулю, что:
,
не равные одновременно нулю, что:
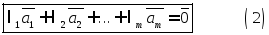
В противном случае векторы называются линейно независимыми (два неколлинеарных вектора).
Пример:
Даны три вектора:
 .
.
Доказать, что
векторы
 и
и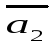 линейно независимы и выразить вектор
линейно независимы и выразить вектор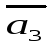 через
через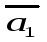 и
и .
.
Решение:
1) Докажем линейную независимость векторов:
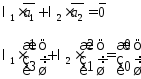
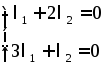
Такая система всегда имеет тривиальное нулевое решение.
Убедимся, что других решений эта система не имеет:
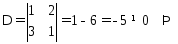 система имеет
только нулевое решение, значит, векторы
линейно независимы.
система имеет
только нулевое решение, значит, векторы
линейно независимы.
2)Выразим
вектор
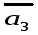 :
:
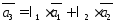
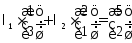
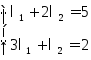
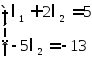
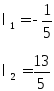
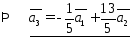
§10.2 Базис и размерность линейного векторного пространства
Определение 1. Линейное пространство R называется n- мерным, если в нем существует n - линейно независимых векторов.
Определение 2. Максимальное число (n) содержащихся в пространстве R линейно независимых векторов называется размерностью пространства и обозначается dim (R).
Обозначение n-мерного пространства: Rn
Определение 3. Совокупность n линейно независимых векторов пространства Rn называется базисом.

Определение 4.
Если
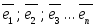 - базис пространстваR,
то вектор
- базис пространстваR,
то вектор
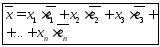 называетсяразложением
вектора
называетсяразложением
вектора
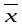 по базису, а числа
по базису, а числа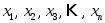 -координатами
вектора
-координатами
вектора
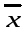 относительно этого базиса.
относительно этого базиса.
§11.1 Скалярное произведение двух векторов в r2 и r3
Определение
1.
Скалярным произведением
двух ненулевых векторов
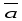 и
и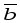 вR2
и R3
называется число, равное произведению
их модулей на
вR2
и R3
называется число, равное произведению
их модулей на
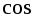 угла между ними.
угла между ними.


Свойства скалярного произведения:
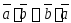 - произведение
векторов коммутативно.
- произведение
векторов коммутативно.
Скалярный квадрат вектора равен квадрату его модуля:
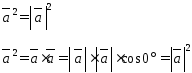
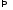

Если
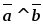 ,
то их скалярное произведение равно
нулю:
,
то их скалярное произведение равно
нулю:


Причем, произведение одноименных орт равно единице, а разноименных орт равно нулю.
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
0 |
1 |
0 |
|
|
0 |
0 |
1 |
Скалярное произведение векторов, заданных координатами равно сумме произведений одноименных координат:

Из формулы скалярного произведения векторов можно найти
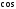 угла между двумя векторами:
угла между двумя векторами:
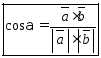
В координатной форме:

Пример:

§11.2 Скалярное произведение двух n-мерных векторов. Евклидово пространство
Определение
1.
Скалярным произведением двух векторов
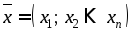 и
и называется число
называется число
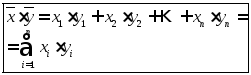
Скалярное
произведение имеет экономический смысл:
если вектор
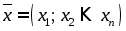 - объем различных товаров, а
- объем различных товаров, а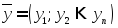 - вектор их
- вектор их
цен, то
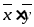 - выражает суммарную стоимость товаров.
- выражает суммарную стоимость товаров.
Скалярное произведение обладает свойствами:
1.
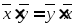 - коммутативность
- коммутативность
2.
 - дистрибутивность
- дистрибутивность
3.
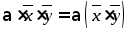 - ассоциативность
- ассоциативность
4.
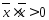 ,
если
,
если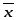 - ненулевой вектор
- ненулевой вектор
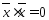 ,
если
,
если
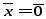
Определение 2. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (аксиомам), называется евклидовым пространством.
Обозначение n-мерного евклидова пространства En
Определение 3.
Длиной или нормой
вектора
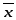 в евклидовом пространстве называется
корень квадратный из его скалярного
квадрата:
в евклидовом пространстве называется
корень квадратный из его скалярного
квадрата:
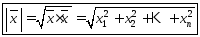
Норма вектора обладает свойствами:
1.
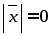 ,
если
,
если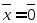
2.
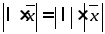 ,
где λ - действительное число
,
где λ - действительное число
3.
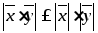 - неравенство Коши-Буняковского
- неравенство Коши-Буняковского
4.
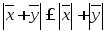 - неравенство треугольника
- неравенство треугольника
В евклидовом
пространстве можно тоже находить
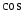 угла между двумя векторами:
угла между двумя векторами:
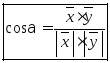 , где
, где
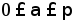 .
.
Из полученной формулы следует, что для n-мерных векторов справедливо определение скалярного произведения, данного для трехмерных векторов.
Определение4:
Скалярным
произведением
двух ненулевых векторов
 и
и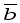 называется число, равное произведению
их длин на
называется число, равное произведению
их длин на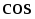 угла между ними.
угла между ними.
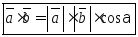
Определение 5. Два вектора называются ортогональными, если их скалярное произведение равно нулю, т.е.
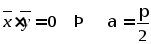
Определение 6. Два вектора считаются коллинеарными если их координаты пропорциональны.
Определение
7.
Векторы
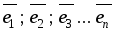 n
- мерного евклидова пространства
образуют ортонормированный
базис,
если эти векторы попарно ортогональны
и норма каждого из них равна единице,
т.е. если
n
- мерного евклидова пространства
образуют ортонормированный
базис,
если эти векторы попарно ортогональны
и норма каждого из них равна единице,
т.е. если
 и
и
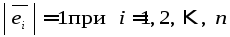
Во всяком n – мерном евклидовом пространстве существует ортонормированный базис.
Пример:
 :
:
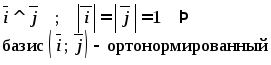
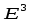 :
: