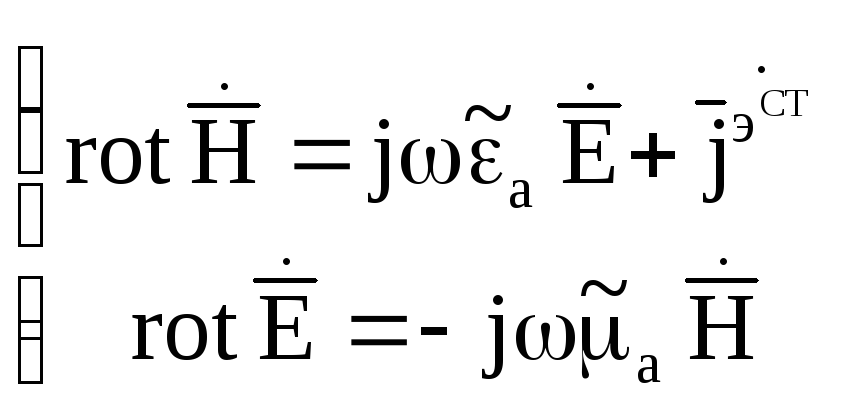6.6. Плоские электромагнитные волны в средах Метод комплексных амплитуд

Любые переменные электромагнитные процессы можно описать с помощью дискретного или непрерывного спектра гармонических электромагнитных полей. Поэтому в дальнейшем будем анализировать гармонические электромагнитные процессы (монохроматические), так как сигнал любой сложности можно представить как суперпозицию гармонических процессов. Обычно используют метод комплексных амплитуд.

Пусть имеется некоторый гармонический процесс _, ему в соответствие ставится , , .

Переход от комплексных амплитуд к исходной величине .

Аналогично и для векторных величин. Пусть есть вектор , ему соответствует комплексная величина или,.

Если мгновенные скалярные и векторные функции удовлетворяют некоторым линейным уравнениям, то этим же уравнениям удовлетворяют и их комплексные аналоги.

Использование метода комплексных амплитуд существенно упрощает решение задач с геометрическими электромагнитными процессами. Причина этого: дифференцирование по времени комплексных амплитуд эквивалентно просто домножению на jw, а интегрирование по времени эквивалентно делению на jw.

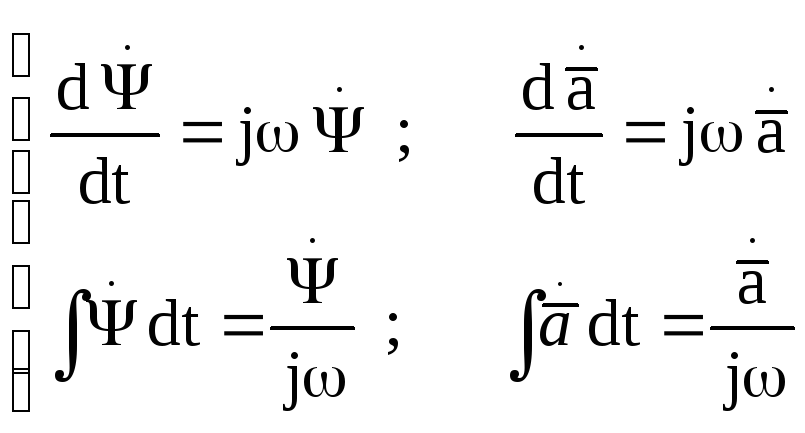
Система уравнений монохроматического (гармонического) поля

Известно, что уравнения Максвелла относятся к линейным дифференциальным уравнениям. При рассмотрении гармонических электромагнитных процессов целесообразно перейти к комплексным амплитудам.

Уравнения Максвелла для монохроматического поля

Если принять , то соответствующие комплексы, где.

Используя понятие комплексных амплитуд, получим

,

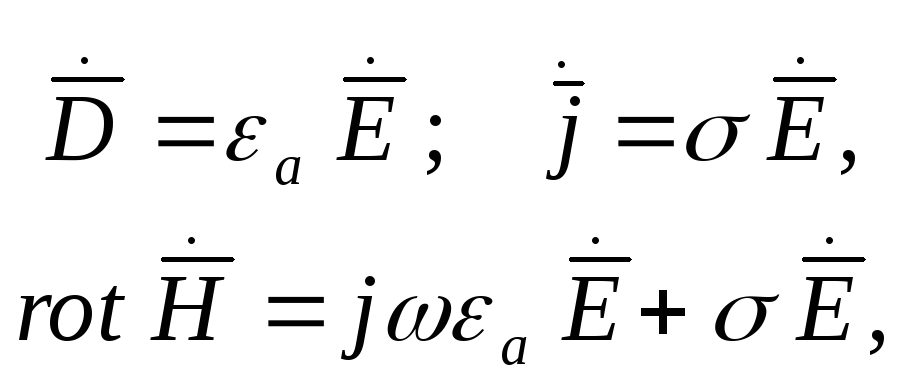
где — комплексная диэлектрическая проницаемость среды.

Входящее в это соотношение отношение называется тангенсом угла электрических потерь.

Комплексная диэлектрическая проницаемость в форме справедлива для сред, в которых имеются только джоулевы потери. В общем случае:

.

Этот общий случай позволяет также учесть потери, связанные с эффектом поляризации в переменном электрическом поле. Наличие диэлектрических потерь приводит к появлению фазового сдвига между электрическими векторами. Величина этого сдвига: .

Рассмотрим 2 уравнение Максвелла: ,

, где ; — тангенс угла магнитных потерь.

Комплексная магнитная проницаемость позволяет учесть магнитные потери, обусловленные эффектом намагничивания вещества в переменном магнитном поле.

В случае гармонического поля при использовании метода комплексных амплитуд возникает дополнительная возможность учесть потери, связанные с эффектами поляризации и намагничивания вещества.

Третье и четвертое уравнения Максвелла, для комплексных амплитуд являются следствием первых двух. В средах с проводимостью, неравной нулю, объемная плотность убывает и в случае установившегося электромагнитного процесса (к ним относятся гармонические колебания). Можно считать, что объемная плотность электрического заряда равна нулю.

.

Это соотношение для среды с конечной проводимостью. Оно является справедливым и для непроводящих сред. Если в непроводящей среде присутствует гармонический процесс, то и изменяется по гармоническому закону:

_.

Всякому изменению объемной плотности соответствует электрический ток в среде. В непроводящей среде возникновение тока невозможно. Поэтому (10) является справедливым в случае гармонических процессов и для непроводящих сред.

Переходя в уравнении к комплексным амплитудам, получим: .

Возьмем дивергенцию от правой и левой части. Аналогично и для четвертого уравнения Максвелла: .

Будем предполагать, что в рассмотренной области имеются сторонние источники.. Для получения справедливых соотношений воспользуемся первым уравнением Максвелла: ,

(6.6.1)

(6.6.2)

Рассмотрим третье уравнение Максвелла. Возьмем дивергенцию от соотношения (1).

.

Для сторонних токов: . Окончательно получим.

В случае гармонических электромагнитных полей

(6.6.3)

Уравнения Максвелла без учета сторонних источников:

Подставляя вторую систему в первую с использованием метода комплексных амплитуд, получим

_.

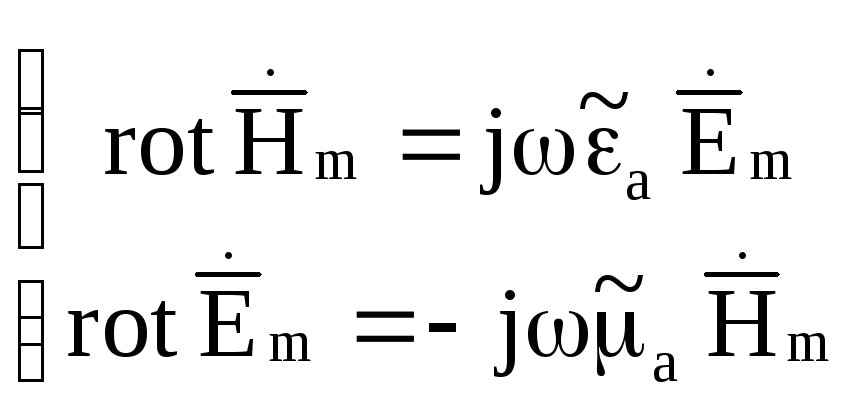В дальнейшем индекс m будем формально опускать.