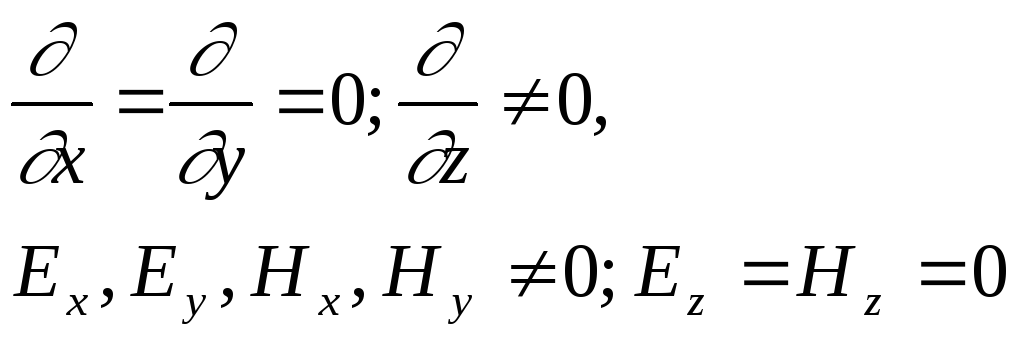Уравнения баланса для средней за период мощности

Теорема Умова-Пойнтинга и соответствующее ей аналитическое соотношение

(6.4.4)

были сформулированы для мгновенных значений и остаются справедливыми в последний момент времени. Это соотношение — важнейшее в классе электродинамики.

При анализе гармонических электромагнитных процессов особый интерес представляют энергетические параметры, усредненные по периоду. Среднее за период значение .

Получим уравнение баланса для среднего за период значения мощности гармонического электромагнитного процесса. Необходимо для каждого из слагаемых уравнения (4) получить среднюю величину. Так как при этом осуществляется интегрирование по времени, а анализируется гармонический электромагнитных процесс, то, естественно, нужно воспользоваться методом комплексных амплитуд. Непосредственная замена мгновенных функций соответствующими комплексными аналогами возможна только в линейных уравнениях. В данном случае непосредственная замена мгновенных функций электромагнитного поля комплексными функциями невозможна, так как выполняются следующие неравенства:

В случае нелинейных уравнений замену мгновенных функций соответствующими комплексными, осуществляют, используя тождество

.

Для начала получим среднее за период значение вектора Пойнтинга

раскроем векторное произведение: .

Таким образом, сумму можно записать как удвоенную действительную часть любого из слагаемых

_.

Величина от времени не зависит. С учетом приведенных рассуждений получаем:

.

Два последних слагаемых, меняются с удвоенной частотой, т.е. половину периода принимают положительную величину, а другую половину — отрицательную. Поэтому и среднее за период значение равно нулю.

(6.6.5)

(6.6.6)

— комплексный вектор Пойнтинга.

(6.6.8)

Итак, выражение (8) определяет среднее за период значение плотности потока энергии через поверхность S. Среднее за период значение потока энергии: .

Средняя за период энергия электрического поля

Уравнения Гельмгольца

Практически все задачи электродинамики разделяют на 2 вида:

1. Прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля;

2. Обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников.

В этом разделе будут рассматриваться основные методы решения прямых задач электродинамики.

Относительно мгновенных значений векторов поля задачи решают очень редко из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений.

Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:

(6.6.9)1 (6.6.10)

Возьмем ротор от правой и левой части соотношения (9). Получим:

(6.6.11)

Воспользуемся известным тождеством: . Из четвертого уравнения Максвелласледует, что

(6.6.12)

Подставим (12) и (10) в (11) и получим: или

(6.6.13)

В результате проведенных преобразований мы получили неоднородное дифференциальное уравнение, которое в математической физике называется неоднородным уравнением Гельмгольца. Это уравнение описывает волновые. процессы. Векторное дифференциальное уравнение (6.6.13) можно записать в виде трех уравнений проекций:

.

Аналогичные уравнения можно получить и для вектора напряженности поля.

,

,

,

Меняя везде знаки, получим:

(6.6.14)

.

При анализе сред, в которых отсутствуют сторонние источники, неоднородные уравнения преобразуются в однородные

(6.6.15)

Уравнения Гельмгольца в форме (13), (14), редко используются при решении электродинамических задач из-за сложной правой части. При решении задач уравнения используются только для полей без сторонних источников. Обычно, если рассматриваются задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. Для них решают электродинамическую задачу, а соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля.

Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:

(6.6.16-19)

Существует следующее векторное тождество:

,

(6.6.20)

Векторную функцию называютвекторным электрическим потенциалом. Соотношение (20) при известном однозначно определяет вектор. Обратное определение не может быть выполнено, т.е. при известном векторном полесоотношение (20) не определяетоднозначно. Известно, что. Поэтому, если ввестии, то соотношение (20) не изменится. Поэтому соотношение (20) определяетс точностью до градиента произвольной функции.

Подставим (20) в (17), получим

или .

Воспользуемся вновь тождеством и. При этом:

.

Скалярную функцию называютскалярным электрическим потенциалом.

Соотношения (13), (14), (15) называются уравнениями Гельмгольца относительно векторов поля.

Будем рассматривать свободные (существующие без сторонних источников) гармонические колебания электромагнитного поля в однородной изотропной среде без потерь. В этом случае удобно воспользоваться однородными уравнениями Гельмгольца относительно векторов электромагнитного поля.

где	(6.6.21-22)

Векторные уравнения (21) и (22) можно записать в виде системы из трех скалярных уравнений:

(6.6.23)

Под волнами подразумевают колебательные движения непрерывных сред. Принципиальные отличия в математическом описании волновых процессов и колебаний токов и напряжений в радиотехнических цепях состоит в том, что для полного описания любой системы достаточно знать конечное число токов и напряжений на различных участках схем. Для полного описания волнового процесса необходимо знать его характеристики в бесконечно большом числе точек в рассматриваемом пространстве. Природа волновых процессов весьма разнообразна: электромагнитные волны, акустические, гравитационные и т. д. Физики полагают, что при распространении любых волн среда постепенно вовлекается в некоторый физический процесс, в результате которого происходит распространение энергии в пространстве.

(6.6.24)

Наиболее просто уравнения (23) и (24) и их решения выглядят в случае рассмотрения плоских электромагнитных волн. Под плоскими подразумевают электромагнитные волны, распространяющиеся вдоль линейной координаты, в каждый фиксированный момент времени неизменные в плоскости, перпендикулярной направлению распространения. Будем полагать, что волна распространяется вдоль оси Z, т.е. вектор Пойнтинга:

(6.6.25)

Из соотношения (25) видно, что вектор Пойнтинга определяется компонентами электромагнитного поля, находящимися в плоскости xOy. В данном случае отсутствуют составляющие поля вдоль оси z. Таким образом, должно выполняться условие: поскольку по определению поле должно быть неизменно в плоскости распространения волны, то

(6.6.26)

Используя соотношение (26), выражения (23) и (24) можно переписать следующим образом

(6.6.27)

(6.6.28)

Решение каждого из уравнений

(6.6.29) (6.6.30)

Для того, чтобы не увеличивать количество постоянных интегрирования, компоненты поля найдем, используя решения (29), (30) и уравнения Максвелла.

,

(6.6.31)

.

Используя соотношение (31), получим:

(6.6.32) (6.6.33)

Вынося jk за скобки, получим:

(6.6.34) (6.6.35)

В итоге получим систему решений:

(6.6.36) (6.6.37)

(6.6.38) (6.6.39)

где , [Ом] — характеристическое сопротивление среды, определяющееся свойствами среды.

Пары (36)-(37) и (38)-(39) образуют вектор Пойнтинга, ориентированный по оси z. Полученные нами решения представляют собой сумму двух слагаемых (так как решалось дифференциальное уравнение). Уточним физический смысл каждого слагаемого. Для этого в уравнении (36) перейдем от комплексных амплитуд к мгновенным значениям.

,

(6.6.40)

Аргумент первого слагаемого — .

Аргумент второго слагаемого — .

Рассмотрим аргументы и слагаемые для t=t₁, z=z₁, т.е. . Дадим приращение времении определим смещение точекэтого волнового процесса с постоянными фазами.

Рисунок 6.6.6 – Движение электромагнитной воны в пространстве.

Для того, чтобы оценить это смещение, рассмотрим следующие равенства:

.

Приводя подобные члены в соотношениях, получим:

,

.

Выражая в первом и втором случаях, получаем:

(6.6.41) (6.6.42)

Соотношение (41) определяет перемещения фиксированной фазы , а соотношение (42) —, т.е. соотношения (41) и (42) определяют фазовую скорость. Соотношение (41) определяет положительную фазовую скорость. Следовательно, компонентыисоответствуют плоской волне, распространяющейся в положительном направлении осиz. Аналогично и в соотношении (42).

Итак, в полученном нами решении (36) первое слагаемое - для плоской волны в положительном направлении, второе слагаемое - в отрицательном.

Уточним физический смысл волнового числа k. Волновое число k показывает изменение фазы волны в радианах при прохождении волной пути в 1 метр. Минимальное расстояние на котором фаза волны изменяется на 2p называется длинной волны (пространственным периодом) :

(6.6.43)

Проанализируем полученные решения на примере ,.

,

.

В этих общих решениях выделим слагаемые, которые соответствуют волне, распространяющейся в положительном направлении оси z:

,

.

Перейдем к мгновенным значениям:

,

.

Из приведенных соотношений следует:

- z = const — это поверхность равных фаз представляет собой плоскость

- Поверхность равных амплитуд совпадает с поверхностью равных фаз (плоская однородная волна)

- В направлении распространения отсутствуют составляющие поля (плоская, однородная, поперечная) Компоненты поля плоской волны взаимноортогональны и перпендикулярны направлению распространения волны.

Между составляющими поля плоской волны существует взаимосвязь.

,

.

Определим энергетические характеристики:

—объемная плотность электрической энергии,

—объемная плотность магнитной энергии.

Так как среда однородная, изотропная и без потерь,

.

Определим скорость распространения энергии:

.

Уравнение для фазовой скорости: , где.

Тогда в случае среды без потерь: .

Различные комбинации полного решения для плоской электромагнитной волны фактически соответствуют одной и той же плоской волне при различных ее ориентациях относительно выбранной системы координат.