Lungu1_math453 / ТФКП Питер[Aleksandrova_E.B.,_Svencickaya_T.A.,_Timofeeva_L.(BookFi.org)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский государственный национальный исследовательский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

б) Аналогично для функции cos7z – первообразной будет функция –

в) Функция

не удовлетворяет условиям Коши-Римана (покажите) и

.pdf

Скачиваний:

Добавлен:

13.04.2015

Размер:

1.4 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>

§4. Первообразная функция

Пусть функция f (z) задана в области D .

Определение 1. Функцию F (z), заданную в области D , назовем пер-

вообразной для функции f (z), если для всех z D выполняется равенство

F ′(z)= f (z).

Из теоремы Коши вытекает следующая важная теорема.

Теорема. Пусть функция f (z) непрерывно дифференцируема в одно-

связной области D . Тогда в этой области существует первообразная F (z)

для функции f (z).

Доказательство. Функция f (z) непрерывно дифференцируема, а

значит аналитическая в области D . Тогда интеграл от f (z) не зависит от пу-

ти интегрирования, а зависит от начальной и конечной точек пути. Зафиксируем точку z0 , выбранную произвольным образом в области D и рассмот-

рим функцию

F (z)= ∫f (z)dz = ∫z		f (ζ )dζ ,	(1)
L	z0

где ζ - промежуточный аргумент, L - любая кривая, соединяющая точку z0

с точкой z , и лежащая в области D . В силу следствия из теоремы Коши функция F (z) однозначно определена.

Покажем, что функция F (z), определенная формулой (1) и есть перво-

образная для функции f (z).

Возьмем приращение ∆z достаточно малым, чтобы z + ∆z D . Так как интеграл не зависит от пути, то соединим точки z и z + ∆z отрезком прямой.

Найдем приращение функции F (z), соответствующее ∆z :

z +∆z	z	z +∆z
∆F = F (z + ∆z)− F (z)= ∫f (ζ )dζ − ∫f (ζ )dζ =		∫f (ζ )dζ .
z0	z0	z

Оценим величину:

		∆F			1	z +∆z


			− f (z)	=		∫f (ζ )dζ − f (z)	,
		∆z	− f (z)	=	∆z	∫f (ζ )dζ − f (z)	,
						z
для чего запишем f (z) в виде:
	1		z +∆z			z+∆z
f (z)=	1		∫f (z)dζ , так как ∫dζ = ∆z ,
f (z)=	∆z		∫f (z)dζ , так как ∫dζ = ∆z ,
			z			z

тогда получим по свойству (5) оценки модуля интеграла (см. §2 данной главы):

∆F

z +∆z

− f (z)

∫

(f (ζ )− f (z))dζ

≤

max

f (ζ )− f (z)

∆z

ζ L

По условию теоремы функция

f (z) непрерывна, это означает, что при

∆z → 0 f (ζ )→ f (z), то есть величина max f (ζ )− f (z) → 0 . А это и означа-

ζ L

ет, что F ′(z)= f (z).

Отсюда следует и еще один факт, что существует неопределенный интеграл от комплексной функции, как совокупность всех первообразных и

обозначаемый ∫ f (z)dz =F (z)+C , где С - любая константа.

Пример 1. Какие из функций имеют первообразные:

а) z 4 + 2i ; б) cos7z ; в) z .

Решение. а) Функция z 4 + 2i непрерывно дифференцируема и пото-

му имеет первообразную z 5 + 2iz ;

потому не является дифференцируемой. Она не имеет первообразной.

z − z0

Для аналитической функции комплексного переменного справедлив аналог формулы Ньютона-Лейбница, которая позволяет вычислить комплексный интеграл от непрерывно дифференцируемой функции в односвязной области, если известна ее первообразная:

∫z

f (t )dt = F (z)− F (z0 ).

Пример 2. Вычислить ∫i

sin z dz .

Решение.

f (z)= sin z . Первообразная этой функции (− cos z), тогда,

применяя формулу Ньютона-Лейбница, получим:

= −cosi + cosπ = −

+ e−i

e + e−1

∫

sin z dz = (− cosz)

iπ

+ 0

§5. Формула Коши

Пусть функция

f (z) является аналитической в односвязной области D

с границей L . Это значит, что функция f (z) имеет определенную конечную производную в каждой точке области D . Формула Коши, которая будет доказана, позволяет выразить значения функции f (z) во всякой внутренней

точке области D через значения этой функции на контуре L . Отсюда вытекает, что значения аналитической функции тесно связаны между собой, так как ее значения вдоль замкнутого контура L вполне определяют ее значения внутри L . Эта формула имеет вид:


f (z0 )=	1			f (z)	dz		(1)

	2πi ∫+z −z0
			L
Доказательство. Введем в рассмотрение функцию
ϕ(z)=		f (z)− f (z0 )				.	(2)

Эта функция является аналитической во всех точках области D , кроме точки z = z0 .

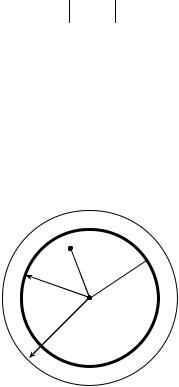
γ		Опишем около точки z0 , как центра, окруж-
z0		Опишем около точки z0 , как центра, окруж-
z0	L	ность γ	произвольно малого радиуса ρ , це-
	L	ность γ	произвольно малого радиуса ρ , це-
	Рис. 10	ликом	лежащую в области D	(рис. 10).
	Рис. 10	Функция ϕ(z) будет аналитической во всех
		Функция ϕ(z) будет аналитической во всех
точках, лежащих между контурами L и γ , включая и сами контуры. Следо-
вательно, на основании теоремы Коши (см. §3) имеем:
		∫ϕ(z)dz = ∫ϕ(z)dz .		(3)
		L +	γ +

Это равенство показывает, что значение ∫ϕ(z)dz не зависит от радиу-

γ +

са ρ вспомогательной окружности γ , будучи постоянным числом, равным

значению ∫ϕ (z )dz . Чтобы определить это постоянное значение, заметим,

L +

что функция ϕ(z) стремится к определенному конечному пределу, когда точ-

ка z стремится к точке z0 .

Действительно, из равенства (2) следует:

lim ϕ(z)= lim		f (z)− f (z0 )	= f ′(z0 ).

z→z0	ζ →0	z − z0
Следовательно, если принять		f ′(z0 ) за значение функции ϕ(z) в точке

z = z0 , то ϕ(z) становится непрерывной функцией всюду в замкнутой облас-

ти D . Значит, ϕ(z) ограничена, то есть ϕ(z) <M , где M - некоторая посто-

янная величина, какова бы ни была точка z области D . Оценим последний интеграл из равенства (3):

∫ϕ(z )dz < M 2π ρ ,

γ +

отсюда следует, что ∫ϕ(z)dz = 0 , так как ρ можно принять сколь угодно

γ +

малым, а значение интеграла есть постоянное число. Иначе из равенства (3) получим:

∫ϕ(z )dz = 0 .

L +

Заменяя ϕ(z) по формуле (2) имеем:

∫

f (z )− f (z0 )

dz = 0

z − z0

L +

или

∫

f (z)

dz − f (z0 )∫

= 0 .

(4)

z −z0

z − z0

L +

Так как в силу примера 2 §2 данной главы ∫

= 2π i , то формула

z − z0

L +

(4) примет вид:

f (z)

dz = f (z0 ) 2πi ,

∫+z −z0

или

f (z0 )

∫

f (z)

dz ,

2π i

z − z0

L +

что и требовалось доказать.

Пример 1. Вычислить интеграл ∫cosz dz, где L - окружность:

L+ z

а) z = 1 ; б) z − 2 = 1 .

Решение. Запишем формулу Коши (1) так, чтобы выражен был сам интеграл:

∫

f (z )

dz = 2π i f (z0 )

(5)

z − z0

L +

а)

f (z)= cosz , z0 = 0 . Контур

= 1 охватывает точку 0, поэтому

∫ cosz

z dz = 2π i cos 0 = 2π i .

L +

cosz

б)

Контур

z − 2

= 1 точку 0 не охватывает, следовательно,

функция

является аналитической в области с границей L , тогда в силу теоремы

Коши интеграл от нее равен 0.

∫ cosz z dz = 0 .

Заметим, что интеграл ∫

cos x

dx , где x - действительная переменная,

является неберущимся.

Для действительной функции действительного переменного из сущест-

вования конечной производной не следует непрерывность этой производной. В случае же функции комплексного переменного имеет место следующее важное утверждение.

Утверждение. Если однозначная функция f (z) комплексного пере-

менного имеет всюду в области D первую производную, то она имеет в этой области и производные всех высших порядков.

Доказательство. Пусть z0 - произвольная точка области D и L -

кусочно-гладкий замкнутый контур, окружающий точку z0 , лежащий со все-

ми своими внутренними точками в области D . Применяя формулу Коши, имеем:

f (z0 )= 21 ∫ f (z) dz. πi L+z −z0

С другой стороны, формальное дифференцирование по параметру z0 в

интеграле типа Коши (1) показывает, что существует производная любого порядка:

′

(z0 )=

∫

′

∫

f (z )

dz ,

2π i

f (z )

2π i

z − z0

(z − z0 )

L +

f ′′(z0 )=

∫

f (z)

dz , f

′′′(z0 )=

∫

f (z )

и т.д.

2π i

− z

2π i

(z − z

L +

Здесь мы опускаем обоснование возможности дифференцирования по параметру z0 под знаком интеграла.

Итак, получили

f (n)(z0 )=

∫

f (z)

dz , n = 1, 2, K

(6)

2π i

(z −z

)n +1

L +

или

∫

f (z )

dz =

2π i

f (n )(z0 ).

(7)

(z − z

)n +1

L +

Замечание. В параграфе «Степенные ряды» этот факт был уже установлен. Формулы (6) и (7) играют важную роль в приложениях.

Пример 2. Вычислить интеграл ∫	z − 2 sin z		dz по контуру
Пример 2. Вычислить интеграл ∫		π 3	dz по контуру
L +	z −
		2

L : z − 1 = 2 .

Решение. В данном случае z0 = π2 , и контур z − 1 = 2 охватывает

точку π2 , поэтому применим формулу (7) и получим:

∫

z − 2 sin z

dz =

2π i

(z − 2 sin z )″

π =

2π i

= 2π i .

z =

z −

Итальянский математик Морера доказал, что верно утверждение, обратное теореме Коши.

Теорема. Если функция f (z), непрерывная в односвязной области D ,

удовлетворяет равенству ∫ f (z )dz = 0 для всякого кусочно-гладкого замк-

L +

нутого контура L , лежащего в этой области, то f (z) является аналитической

в области D .

Доказательство. Действительно, мы видим (§4 данной главы), что

при условиях этой теоремы интеграл ∫z		f (ζ )dζ	не зависит от пути, соеди-
	z0
няющего точки z0	и z в области D , и определяет функцию F (z), аналитиче-
скую в области D	′		′
	, причем F (z)= f (z). Так как функция F (z) как произ-
водная функции, аналитической в области D , есть функция, аналитическая в
	′		аналитическая в области D .
этой области D , то f (z)= F (z) есть функция,

Теорема доказана.

ГЛАВА IV. Ряды Тейлора и Лорана. Вычеты и их применение

§1. Ряд Тейлора

В §5 главы II было показано, что сумма степенного ряда является аналитической функцией внутри круга сходимости. Справедливо и обратное утверждение.

Теорема. Функция f (z), аналитическая внутри круга z − z0 < R , явля-

ется в этом круге суммой степенного ряда

∞

f (z)= ∑cn (z −z0 )n .

n=0

Доказательство. Пусть D

- круг:

z − z0

< R . Рассмотрим произ-

вольную точку z D . Проведем окружность C ρ

с центром z0

и радиусом ρ ,

причем ρ выберем так, чтобы выполнялось

условие

z − z0

< ρ < R (см. рис.1).

|z-z0|

|ξ-z0|

Ясно, что C ρ D . Значение функции в

точке z вычисляется по формуле Коши (см.

Cρ

гл. 2, §5).

f (z)=

∫

f (ξ)

dξ .

Рис. 1

(1)

2π i

ξ −z

C ρ

Преобразуем дробь

следующим образом

ξ − z

− (z − z

)

ξ − z

1 −

z − z0

ξ − z0

Поскольку

z − z0

< 1 для ξ C ρ

(см. рис.1),

выражение

ξ − z0

1 −

z − z0

ξ − z0

можно рассматривать как сумму ряда геометрической прогрессии со знаменателем по модулю меньшим единицы. Тогда

1		1	∞	z − z0	n
	=					,

ξ − z			∑	ξ − z0
		ξ − z0 n=0

причем написанный ряд равномерно сходится на C ρ , так как мажорируется

∞

z − z0

сходящимся числовым рядом

∑

. Подставляя представление для

n+1

n=0

дроби

в формулу (1), получим:

ξ − z

f (ξ)

f (z)=

f (ξ)

(z −z0 )+K+

(z −z0 )n +K dξ .

2π i

(ξ

−z0 )2

(ξ

−z0 )n +1

∫+ ξ −z0

C ρ

∞

f (ξ)

(z − z0 )n ,

Очевидно, что ряд

также сходится равномер-

∑n =0 (ξ − z0 )n +1

но по ξ , а, следовательно, его можно почленно проинтегрировать вдоль C ρ

(см

). Тогда

f (z)=

f (ξ)

dξ +

f (ξ)

dξ (z − z0 )+K=

2π i

∫+ (ξ − z0 )2

∫+ ξ − z0

C ρ

∞

f (ξ)

= ∑

dξ (z −z0 )n .

n +1

n =0 2π i

∫+ (ξ −z0 )

C ρ

Мы получим:

∞

f (z)= ∑cn (z −z0 )n ,

(2)

n=0

где c

f (ξ)

dξ,

n = 0, 1, 2, K

(3)

2π i ∫+ (ξ − z0 )n +1

C ρ

Значит, f (z) представима в виде степенного ряда.

Замечание 1. В силу теоремы Коши, в формуле (3) окружность C ρ

можно заменить любым замкнутым контуром C ,

лежащим в D и содержа-

щим точку z0 внутри.

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>