матан 3 курс 2013 / лекции / 212

lim Sn (x)= S(x).

n→∞

Глава 12 Функціональні послідовності й ряди

1

Глава 12 Функціональні послідовності й ряди § 1. Означення функціональної послідовності й функціонального ряду

Означення. Функціональною послідовністю називається впорядкована

послідовність функцій зі спільною областю визначення

f1 (x), f2 (x), f3 (x), …, fn (x), … де x D({fn }).

Означення. Точка x0 D({fn }) називається точкою збіжності функціональної

послідовності, якщо числова послідовність f1 (x0 ), f2 (x0 ), f3 (x0 ), …, fn (x0 ), … збігається. Сукупність усіх точок збіжності утворює область збіжності X .

Означення. На області збіжності X можна ввести функцію

f (x) = lim fn (x) ,

n→∞

яку будемо називати граничною функцією.

Паралельно ми будемо розглядати функціональні ряди, тобто ряди, членами яких є функції.

Означення. Ряд, складений з функцій, називається функціональним рядом

∞

∑un (x)= u1 (x)+... + un (x)+...

n=1

Спільна область визначення функцій un (x) називається областю визначення функціонального ряду й позначається D({un }).

∞

Означення. Множина точок збіжності ряду ∑un (x) називається областю

n=1

збіжності й позначається X .

Означення. На області збіжності X можна ввести означення суми ряду, як деякої функції від x :

∞

∑un (x) = S(x).

n=1

Установимо зв'язок між функціональним рядом і функціональною послідовністю.

∞

Нехай дано функціональний ряд u1 (x)+ u2 (x)+... + un (x)+... = ∑un (x).

n=1

Введемо означення послідовності часткових сум як

S1 (x)= u1 (x)

S2 (x)= u1 (x)+ u2 (x)= S1 (x)+ u2 (x)

. . . . . . . . . . . . . . . . .

n

Sn (x)= ∑ui (x)= Sn−1 (x)+ un (x)

i=1

. . . . . . . . . . . . . . . . .

оскільки ряд збігається в кожній точці x X , то й послідовність часткових сум {Sn (x)}збігається на всьому X , тобто існує границя

Установимо зворотну залежність: нехай дана послідовність {fn (x)}, побудуємо функціональний ряд

Глава 12 Функціональні послідовності й ряди

u1 (x)= f1 (x) u2 (x)= f2 (x)−

. . . . . . . . .

un (x)= fn (x)−

. . . . . . . . . .

n

При цьому часткові суми ряду ∑ui =

i=1

2

f1 (x)

fn−1 (x)

fn (x) будуть збігатись на X , оскільки

це область збіжності послідовності.

Виходить, що, довівши який-небудь результат для функціональної послідовності, ми можемо його переформулювати для функціонального ряду й навпаки.

Тому дослідження функціональних послідовностей і рядів будемо проводити паралельно.

§ 2. Рівномірна збіжність

Вище ми означили поточкову збіжність функціональної послідовності, тобто збіжність числової послідовності в кожній точці області збіжності.

	На основі цього означення беремо x1 X ,			і для кожного ε > 0 знаходимо
номер N1 (ε) (він існує) такий, що для				кожного n > N1 виконується
	fn (x1 )− f (x1 )		< ε .

Тут x1 - заздалегідь фіксована точка.

Візьмемо іншу точку x2 X . Одержимо нову числову послідовність і для того ж самого ε > 0 , що й для попередньої точки x1 X знайдеться новий номер N2 (ε), який не обов'язково збігається з N1 , після якого виконується fn (x2 )− f (x2 ) < ε .

Продовжимо цей процес нескінченно. Перебравши всі x X , для кожного знайдемо за заданим ε > 0 свій номер N .

Така збіжність називається поточковою. Тут номер залежить не тільки від ε , але й від обраної точки x .

Виникає питання: чи знайдеться такий номер N , який би для даного ε , задовольняв би всім x одразу, або такого номера не існує?

Якби точок у множині X була скінчена кількість (100; 1000; ...) , то, обравши

зцієї множини номерів найбільший, ми б одержали номер, що задовольняє всім

xX .

Але в нас X - це або інтервал, або відрізок - тобто змінна x приймає

нескінченну множину числових значень, тобто наша функціональна послідовність містить у собі нескінченну множину числових послідовностей. Для кожної з них знайдеться свій номер N , і цих номерів буде нескінченно багато.

Повторюємо питання: чи знайдеться такий номер N , що (при заданому ε )

задовольняв би всім послідовностям? Відповідь: не завжди. Покажемо на прикладах.

Глава 12 Функціональні послідовності й ряди

3

Приклад

1.

Дослідити

на

збіжність

функціональну

послідовність

fn (x)=

x

на відрізку [0; 1].

+ n2 x2

1

Спочатку встановимо поточкову збіжність.

При x = 0 ,

fn

(x)= 0 → 0 ,

При x (0; 1],

fn (x) прямує до нуля якщо n → ∞ , тобто

на [0; 1].

lim fn (x)= f (x)≡ 0

n→∞

Поточкова збіжність є. Спробуємо

знайти спільний номер, що задовольняє

всім x . Помітимо, що 2nx ≤1 + n2 x2

й

0 ≤ fn (x)=

1

2nx

≤

1

.

2n

+ n2 x2

1

2n

Звідси видно,

що

f (x)<ε ,

якщо

1

1

виконано

n < ε , тобто при n >

= N ,

2

2ε

причому відразу для всіх x [0; 1]. Знайшовся номер, що задовольняє всім x .

Приклад

2.

Дослідити

на

збіжність

функціональну

послідовність

fn (x)=

nx

на відрізку [0; 1].

+ n2 x2

1

Спочатку встановимо поточкову збіжність

При x = 0 ,

fn

(x)= 0 → 0 ,

при x (0; 1]

fn (x) прямує до нуля при n → ∞ , тобто

[0; 1].

lim fn (x)= f (x)≡ 0

на

n→∞

Поточкова збіжність є.

Спроби знайти спільний номер не

дають результату

2nx

fn (x)

=

1

≤

1

(<ε)

не

2

1 + n2 x2

2

виходить при ε ≤

1

.

2

1

Покажемо, що спільного номера

для всіх

x

немає,

оскільки, вибравши

ε =

й

взявши

будь-який, як завгодно

1

2

великий

номер

n ,

для елемента

xn

=

[0; 1]

одержимо

числову послідовність

n

{fi (xn )},

n , що

серед якої знайдеться елемент з як завгодно великим номером

fn (xn )=

1

.

2

існує такий елемент xn [0; 1], що

fn (xn )

Тобто для будь-якого номера n

= ε .

А тому спільного номера, починаючи з якого виконується

fn (x)

< ε ,

і який би

підійшов відразу для всіх x немає.

Оскільки при будь-якому фіксованому x X

lim Sn (x)= S(x), то для залишку ряду lim ϕn (x)= 0 .

n→∞ n→∞

∞

ϕn (x)= ∑ui (x)= S(x)− Sn (x).

i=n+1

Глава 12 Функціональні послідовності й ряди						4
	Означення.			Кажуть, що послідовність {fn (x)} збігається рівномірно на X ,
якщо вона має в X				граничну функцію	f (x), і для кожного ε > 0 існує номер N(ε),
що не залежить				від x , такий, що	для кожного	n > N виконано нерівність
	fn (x)− f (x)		< ε (відразу для всіх x X ). Позначення:			fn (x) f (x).

∞

Перенесемо зараз усе сказане на випадок функціонального ряду ∑un (x).

n=1

Припустимо, що ряд збігається на множині X , тобто, збігається числовий ряд

∞

∑un (x0 ) у кожній точці x0 X . Введемо поняття залишку ряду

n=1

границя часткових сум

Якщо послідовність часткових сум рівномірно збігається Sn (x) S(x) на множині X , або, що те ж саме, залишок ряду ϕn (x) 0 , то кажуть, що ряд збігається рівномірно.

	∞
Означення. Функціональний	ряд ∑un (x), що збігається	на множині X ,
	n=1
називається рівномірно збіжним на	X , якщо для кожного ε > 0 існує номер N(ε),
що не залежить від вибору точки x	такий, що при n > N виконано		Sn (x)− S(x)		<ε

або, що рівносильне ϕn (x) <ε , тобто

∞

Позначення: ∑un (x) S(x).

n=1

∞

∑ui (x) <ε для всіх x з X одночасно.

i=n+1

Перш ніж сформулювати критерій Коши для функціональних послідовностей,

введемо поняття, яке аналогічно фундаментальності.

Означення.

Кажуть,

що

функціональна

послідовність

задовольняє

«Ф-властивості», якщо для кожного ε > 0 існує номер N(ε), що не залежить від x ,

такий, що для будь-яких

n, m > N

виконано

fn (x)− fm (x)

< ε

для

всіх

x X

відразу.

Теорема (Критерій Коши).

Для того

щоб

функціональна послідовність

{fn (x)} була збіжною на

X

рівномірно, необхідно й

достатньо,

щоб вона

задовольняла «Ф-властивості».

Доведення.

□ Необхідність. Зафіксуємо

додатне

ε й

будемо

шукати

номер N . Нехай наша функціональна послідовність рівномірно збігається

fn f

на множині X . Тоді для кожного ε > 0 (для нашого фіксованого ε )

існує номер

N(ε) такий, що для кожного n > N виконано

fn (x)− f (x)

< ε

, відразу для всіх x із

2

Глава 12 Функціональні послідовності й ряди

5

множини X . Аналогічно, для будь-якого номера m > N виконано

fm (x)− f (x)

<

ε .

Але тоді номер N(ε) є саме той номер,

2

що ми шукали, оскільки при всіх n, m > N

виконано

fn − fm

≤

fn − fm

+

fm − f

<

ε

+ ε

=ε , відразу для всіх x X .

2

2

послідовність {fn (x)} володіє «Ф-

Достатність. Нехай функціональна

властивістю».

1)Доведемо спочатку поточкову збіжність. Для цього візьмемо довільну точку

xX . У цьому випадку наша функціональна послідовність перетворюється в числову. За умовою теореми вона фундаментальна (це випливає з “Ф-властивості”),

азначить, за критерієм Коши для числових послідовностей, наша послідовність збігається. Оскільки в якості x ми взяли довільну точку, то ми довели збіжність

(поточкову) на всьому X .

f (x)= lim fn (x) для всіх x X .

Тобто довели існування граничної функції

n→∞

2) Доведемо рівномірну збіжність функціональної послідовності. Оскільки для

будь-яких n, m > N

виконано нерівність

fn (x)− fm (x)

<

ε , для всіх x відразу й

2

номер m може бути будь-яким, то спрямуємо

m → ∞ .

Помітимо, що має місце

поточкова збіжність

lim fm (x)= f (x) за доведеним вище. У результаті граничного

m→∞

≤ ε

переходу в нерівності одержимо

fn (x)− f

(x)

< ε . ■

2

Переформулюємо критерій Коши для функціональних рядів.

Теорема (Критерій Коши рівномірної збіжності функціонального ряду).

∞
Для того щоб ряд ∑un (x) був збіжним рівномірно на множині X , необхідно й
n=1
достатньо, щоб для кожного ε > 0 існував номер N(ε) такий, що для будь-яких
n, m > N виконувалася нерівність
n+m	(x) = un+1	(x)+... +un+m (x) < ε
∑uk
k =n+1

для всіх x X відразу.

Критерій, проте, дуже незручний для користування, і на практиці за звичаєм, користуються більш простими ознаками рівномірної збіжності.

Наступний критерій дуже зручний у застосуванні при перевірці рівномірної

збіжності послідовності.

fn (x) f (x) необхідно й достатньо, щоб числова

Теорема. Для того щоб

послідовність M n

= sup

fn (x)- f (x)

була збіжною до нуля lim M n

= 0 .

x X

n→∞

Доведення.

□

Необхідність.

Нехай

fn (x) f (x),

тоді

ε > 0 N (ε):

n > N виконується

fn (x) − f (x)

<ε для всіх x X відразу.

Оскільки це виконано

x X , то

візьмемо

точну

верхню

межу

sup

fn (x) − f (x)

≤ε , що й було потрібно довести.

n

Глава 12 Функціональні послідовності й ряди			6
	Достатність. Нехай	M n → 0 , тобто	ε > 0 N(ε): n > N

sup

fn (x) − f (x)

<ε . Але якщо точна верхня межа sup

fn (x) − f (x)

< ε , то будь-яке

x

x

значення

функції

не

перевищує

своєї

точної

верхньої

межі

fn (x) − f (x)

≤ sup

fn (x) − f (x)

<ε , а тому й менше ε . ■

x

fn (x)= xn на

Приклад 1. Дослідити на рівномірну збіжність послідовність

[0; 1].

x [0; 1)

1.

Знайдемо граничну функцію

f (x) = lim

f (x) =

0,

.

x =1

n→∞

1,

2.

Знайдемо M n (x) =

fn (x) − f (x)

=

xn ,

x [0; 1)

.

x =

1

0,

3.

Знайдемо M n = sup M n (x) =1 - точна верхня межа.

x

4.

Знайдемо lim M n

=1 ≠ 0 . Немає рівномірної збіжності.

Приклад 2.

n→∞

Дослідити

на

рівномірну

збіжність

послідовність

fn (x)= 2n2 xe−n2 x2 на [0; 1].

1.

Знайдемо граничну функцію f (x) = lim f (x) ≡ 0 (можна за Лопиталем).

n→∞

2.

Знайдемо M n (x) =

fn (x) − f (x)

= 2n2 xe−n2 x2 .

3.

Щоб знайти супремум (глобальний екстремум)

обчислимо похідну:

M n′(x) = 2n2e−n2 x2 (1 −2n2 x2 )= 0 . Підозрілими

точками є

x = 0 , x =1

і xn =

1 .

2 n

−

1

Тоді M n

= sup M n (x) = M n (xn ) =

2 n e

2

- точна верхня межа.

x

4. Знайдемо lim M n = ∞ ≠ 0 . Немає рівномірної збіжності.

n→∞

Для функціональних рядів частіше будемо користуватись наступною ознакою рівномірної збіжності.

			∞
Теорема (Ознака Вейерштрасса). Нехай дано ряд ∑un (x). Якщо
			n=1		un (x)			≤ cn
1) Члени функціонального ряду		задовольняють умовам							для
кожного n =1, 2, 3, … в області X .
	∞
2) Ряд із мажоруючих констант ∑cn		збігається,
	n=1
	∞
то тоді функціональний ряд ∑un (x) збігається на множині X				рівномірно.
Доведення.	n=1
	□ Скористаємося критерієм Коши.		Візьмемо ε > 0 ,			зафіксуємо
									∞
його й знайдемо	номер N . Оскільки	за другою	умовою теореми			ряд			∑cn

n=1

Глава 12 Функціональні послідовності й ряди

7

збігається, то за критерієм Коши для числових рядів він задовольняє наступній властивості («Ф-властивості»): для кожного ε > 0 (для нашого фіксованого ε ) існує

n+m

номер N(ε) такий, що для будь-яких n, m > N виконане нерівність ∑ci

<ε .

i=n+1

Покажемо, що цей номер N(ε) і є той, який ми шукаємо, шуканий.

властивість1

n+m

n+m

↓

n+m

∑ui (x)

≤

∑

ui (x)

≤

∑ci < ε

i=n+1

i=n+1

i=n+1

∞

і за критерієм Коші для функціональних

рядів, наш ряд

∑un (x)

збігається

рівномірно на X . ■

n=1

∞

Приклад. Функціональний ряд

∑

sin nx

збігається

рівномірно на всій

2

n=1

n

∞

sin nx

1

1

числовій вісі, оскільки виконано нерівність

≤

, а мажоруючий ряд ∑

2

2

2

n

n

n=1

n

збігається.

Поряд із мажорантною ознакою Вейерштрасса, своєрідним аналогом якого в теорії довільних числових рядів була абсолютна збіжність, сформулюємо ще дві ознаки рівномірної збіжності функціонального ряду, аналоги яких ми вивчали в теорії числових рядів.

Ознаки Абеля й Дирихле

Розглянемо ряд

∞

∑an (x)bn (x)= a1 (x)b1 (x)+ a2 (x)b2 (x)+…+ an (x)bn (x)+…

n=1

де {an (x)}й {bn (x)} - дві послідовності функцій від x на множині X .

Ознака Абеля. Якщо

∞

1) ряд ∑bn (x)= b1 (x)+b2 (x)+…+bn (x)+… збігається рівномірно в області

n=1

X ,

2) функції an (x) утворюють монотонну послідовність при кожному x X й у сукупності (тобто при будь-яких x і n ), обмежені an (x) ≤ K ,

∞

то ряд ∑an (x)bn (x) збігається рівномірно в області X .

n=1

Ознака Дирихле. Якщо

∞

1) часткові суми ряду ∑bn (x) в сукупності (при будь-яких x і n ) обмежені:

n=1

n

∑bi (x) ≤ M ,

i=1

	Глава 12 Функціональні послідовності й ряди		8
	2) функції an (x) утворюють (при кожному x ) монотонну послідовність, що
	збігається до нуля рівномірно в області X ,
	∞
	то ряд ∑an (x)bn (x) збігається рівномірно в області X .
	n=1
	∞	sin nx
	Приклад. Дослідити на рівномірну збіжність ряд ∑		на відрізку
		n
	n=1
	[ε; 2π −ε]. Скористаємося ознакою Дирихле:

1)послідовність 1 монотонно спадає й прямує до нуля, а оскільки вона

n

числова, то прямує до нуля рівномірно;

∞

2) часткові суми ряду ∑sin nx можна оцінити, скориставшись формулою для

n=1

n

∑sin k з § 7 глави 11:

k =1

(n +1)x sin

n

n

sin

x

1

1

∑sin kx

=

2

2

≤

≤

.

x

1

ε

1

k =1

sin

sin

x

sin 2

∞

2

2

sin nx

рівномірно збіжний на відрізку [ε; 2π −ε] за ознакою

Відповідь. Ряд ∑

n

n=1

Дирихле.

§ 3. Властивості рівномірно збіжних послідовностей і рядів Властивість 1. Неперервність суми ряду

Теорема. Якщо 1) члени ряду un (x) - неперервні на X функції;

∞

2) ряд рівномірно збіжний ∑un (x) S(x) на X ;

n=1

то сума ряду S(x) - неперервна на X функція. Доведення. □ Введемо позначення:

∞	n	∞
S(x)= ∑ui (x)= ∑ui (x)+		∑ui (x)= Sn (x)+ϕn (x),
i=1	i=1	i=n+1
тут ϕn (x) - залишок ряду.

∞

За умовою функціональний ряд ∑un (x) збігається рівномірно на X , що

n=1

рівносильне рівномірної збіжності до нуля залишку ряду ϕn (x) 0 на X (за

означенням рівномірної збіжності ряду).

Візьмемо довільну точку x0 X й покажемо неперервність функції S(x) в цій точці, тобто що для кожного ε > 0 існує δ(ε) таке, що для кожного x : x − x0 <δ виконано

Глава 12 Функціональні послідовності й ряди

S(x)− S(x0 )

<ε

9

Перетворимо в останній нерівності ліву частину.

S

(x)− S(x0 )

≤

Sn (x)− Sn (x0 )

+

ϕn (x)

+

ϕn (x0 )

і будемо оцінювати отримані

доданки. Для цього візьмемо ε > 0 , зафіксуємо, і будемо шукати δ .

Оцінимо другий і третій доданок: оскільки залишок ряду ϕn (x) 0

на X , то

за

нашим фіксованим ε

знайдеться такий

номер

N ,

що при n > N

виконано

ϕ

n

(x)

<

ε й

ϕ

n

(x )

< ε .

3

0

3

n

Зафіксуємо номер

і оцінимо перший доданок.

Зараз будемо розглядати

часткові суми Sn (x) й Sn (x0 ) тільки з цим фіксованим номером n > N .

Часткова сума Sn (x) складається з

n

(скінченої кількості) неперервних

доданків, а тому неперервна на

X , і, зокрема,

у точці

x0 , а значить по нашому

фіксованому ε

знайдеться δ > 0 таке, що

x − x0

<δ =>

Sn (x)− Sn (x0 )

< ε .

3

Тепер підставимо оцінки доданків у нашу основну нерівність і одержимо

S

(x)− S(x0 )

<ε як тільки

x − x0

<δ . Шукане δ

знайшлося! ■

Перефразуємо теорему на мову послідовностей.

X функцій {fn (x)} збігається

Теорема. Якщо послідовність неперервних на

рівномірно до граничної функції

f (x), то f (x) - неперервна.

Зауваження. Легко показати, що якщо послідовність функцій збігається

нерівномірно, то її гранична функція не обов'язково неперервна.

Приклад 1. Нехай дана функціональна послідовність {fn (x)}= {xn }на [0; 1].

Гранична функція lim

fn (x)= f (x)= 0,

x [0 , 1) розривна.

n→∞

1,

x =1

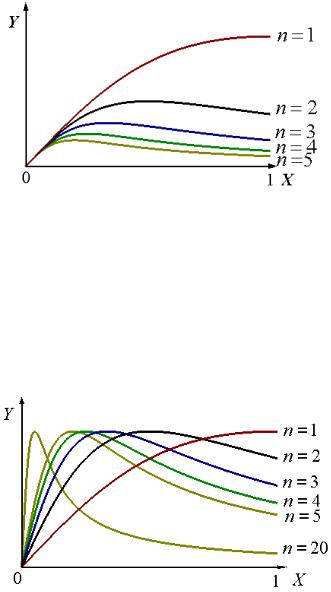
Проте, у деяких випадках нерівномірна збіжність послідовності неперервних

функцій може давати й неперервну границю.

nx

Приклад 2. Нехай дана функціональна послідовність {fn (x)}=

на

[0; 1]. Гранична функція

lim fn (x)= f (x)≡ 0

1 + n2 x2

неперервна. Але послідовність {fn (x)}

n→∞

f (x) нерівномірно (дивися приклад 2 на минулій

збігається до граничної функції

лекції у § 2 рівномірній збіжності).

У той же час наведемо приклад послідовності розривних функцій, що збігаються рівномірно до неперервної функції.

Глава 12 Функціональні послідовності й ряди											10
Приклад					3. Нехай дана	функціональна	послідовність		{fn (x)} на		[0; 1],
		1		,	x ≥ 0
fn (x)= n							lim fn (x)= f (x)≡ 0
					. Гранична функція					неперервна.
	1			,	x < 0		n→∞
	2n
							1
Рівномірна збіжність установлюється легко: N =								.
							ε
Більше того, можна взяти послідовність розривних функцій, що сходяться
нерівномірно, а граничну функцію одержати неперервну.									{fn (x)} на		[0; 1],
Приклад					4. Нехай дана	функціональна	послідовність

				nx
					2		2
fn (x)= 1			+ n			x
		1		,
n

				1
,	x 0 ,					lim f		(x)= f (x)≡ 0 неперервна.
				n . Гранична функція			n
	1					n→∞
	x		, 1
	n

Однак, за аналогією із прикладом 2 неважко встановити відсутність рівномірної збіжності.

Висновок. Попередня теорема каже, що якщо всі функції fn - неперервні, то

для неперервності граничної функції достатньо рівномірної збіжності.

Однак приклад 2 показує, що ця умова не є необхідною: ми мали неперервні функції fn й одержали неперервну граничну функцію f , хоча рівномірної збіжності

не було.

Більше того, 3 і 4 приклади показують, що функції fn можуть бути розривними, сходитися як рівномірно, так і нерівномірно, а гранична функція f

однаково може виявитися неперервною.

Проте існують випадки, коли рівномірна збіжність все-таки виявляється необхідною.

∞

Теорема (Дині). Нехай 1) Усі члени ряду ∑un (x) неперервні на X ,

	n=1
(додається умова)	2) un (x)≥ 0 на X ,
	∞
	3) ряд збігається ∑un (x)= S(x) на X ,
	n=1
	4) S(x) неперервна на X ,

∞

то тоді ряд збігається рівномірно ∑un (x) S(x) на X .

n=1

Властивість 2. Почленне інтегрування ряду Теорема. Якщо 1) функції un (x) неперервні на [a; b] й

∞

2) складений з них ряд ∑un (x) збігається на [a; b] рівномірно,

n=1

то існує інтеграл від суми ряду, і він дорівнює сумі інтегралів