1. Найти сумму матриц

+ ==.

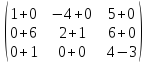Сложение матриц произведено по известному правилу. Обе слагаемые матрицы являются треугольными (одна  нижняя, другая  верхняя).

2. Умножить матрицу на число

3==.

3. Посчитать результат арифметических операций над матрицами

2==.

4. Умножить вектор-строку на вектор-столбец

= 01 + 12 + 2 0 = 2

и вектор-столбец на вектор-строку

= =.

Эти примеры еще раз демонстрируют не коммутативность произведения матриц, т.е. зависимость результата от порядка сомножителей.

5. Найти произведение двух матриц

= =

= .

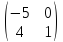Системы линейных уравнений

Решить системы линейных уравнений методом Гаусса

Действуя по методу Гаусса, составим расширенную

матрицу, приведем ее левую секцию к единичной

матрице, в правой секции найдем решение системы.

.

Следует помнить, что на каждой стадии преобразований расширенной матрицы аналогичные действия производятся над соответствующими уравнениями. Поэтому в любой момент каждую строку расширенной матрицы можно прочитать как уравнение, коэффициентами которого являются элементы строки. Поступив так, получим =2, =3,=2.

Прямой подстановкой в уравнения нетрудно убедиться в том, что найденные значения неизвестных в самом деле являются решением системы.

.

Нулевая строка свидетельствует о том, что система является неопределенной. Выражая две первые переменные через третью, найдем

Последняя строка, читаемая как уравнение, даст результат "0=2", который может быть истолкован как противоречие. Однако на самом деле это противоречие мнимое. Преобразования метода Гаусса подбирались по принципу сохранения равенств. В случае несовместности системы одновременное выполнение всех равенств невозможно ни при каких значениях переменных, т.е. среди равенств, по крайней мере, одно будет неравенством. Результатом сложения неравенства с равенством будет, конечно же, неравенство, чем и объясняется отсутствие противоречия в последней строке. Cтрока подобного типа является признаком несовместности системы уравнений.

является признаком несовместности системы уравнений.

Векторная алгебра

1. Дан треугольник с вершинами в точках A (1,2), B (7,10), C (-1,3).

Найти и определить он острый или тупой?

Для решения задачи сначала построим символический треугольник с вершинами в точках А, В и С безотносительно к системе координат, поскольку важен только общий принцип вычислений. Угол А=φ при вершине А образован сторонами треугольника АВ и АС или, что то же самое, является углом

между векторами и . Координаты этих векторов находим путем вычитания соответствующих координат конечной и начальной точек: =(6, 8), =(2, 1). Использование формулы скалярного произведения дает

= ==⇒ cos φ < 0 ⇒ A – тупой в отличие от рисунка.

2. Даны векторы =+2и=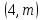. Найти значения параметраm, при которых ‖ 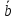и⊥ .

Сначала для единообразия запишем первый вектор в координатной форме, т.е. =. Далее, используя пропорциональность координат коллинеарных векторов, находим = . Наконец, раскрывая пропорцию, получаем уравнение =8, откудаm==.

Признаком ортогональности векторов является равенство нулю их скалярного произведения 0==4m+2m=6m, откуда находим m=0. При графической иллюстрации геометрической сути этой задачи рассмотрим возможные расположения векторов в системе координат. На рисунке векторы изображены с совмещенными началами при отрицательных значениях параметра m = 2. Варьирование величиной m влечет одновременное вращение векторов в противоположных направлениях с перемещением концевых точек вдоль соответствующих пунктирных линий. Коллинеарность и ортогональность векторов возникает при вычисленных значениях m.

Аналитическая геометрия

1. Найти уравнение прямой линии l, проходящей через точку =(1, 2) перпендикулярно направлению=(1, 3). В компактной записи – найти l: ∊l  . Поскольку по условию задачи в качестве нормального вектора искомой прямой может быть выбран вектор =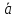, то коэффициентами при переменных в уравнении прямой будут координаты этого вектора

l : .

Используя факт прохождения прямой через заданную точку, найдем С путем подстановки в уравнение ее координат 1+32+С=0, откуда находим С= 5. Тогда

l : .

Направляющим вектором такой прямой будет любой вектор, ортогональный нормальному. Этому условию удовлетворяет вектор = (3, 1).

Упражнение. Найти ее каноническое и параметрические уравнения.

2. Построить прямую : (1, 2)∊ ∥ . В этом случае вектор может быть принят в качестве направляющего вектора, т.е.=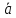. Такие исходные данные позволяют сразу же построить каноническое уравнение прямой

:

и параметрические уравнения + 3t.

Упражнение. Из канонического получить общее уравнение прямой.

3. Найти уравнение прямой :∊ ‖.

Требование параллельности прямых означает коллинеарность нормальных векторов и прямых и, вследствие чего можно принять= =(3, 1). Тогда коэффициенты при переменных в искомом уравнении известны : 3x+y+С=0, а для определения свободного члена уравнения достаточно воспользоваться фактом ∊ , подставив координаты точки в уравнение 31+2+С=0, откуда находим С= 5. В итоге записываем искомое уравнение прямой

: 3x+y5=0.

4. Найти :∊ ⊥. Используя перпендикулярность прямых можно принять =. Таким исходным данным наилучшим образом отвечает каноническое или параметрические уравнения:

.

Упражнение. Построить все остальные уравнения прямой.

5. Найти уравнение прямой, проходящей через точки (1, 1) и(2,3). В качестве направляющего вектора естественно принять

==(3, 2). Тогда по обкатанной схеме получим параметрические уравнения и общее уравнение 2x+3y5=0. Прямой подстановкой нетрудно проверить, что обе заданные точки действительно удовлетворяют общему уравнению, которое тем самым определяет искомую прямую.

6. Геометрическая интерпретация решения системы линейных урав-нений. Ранее в качестве простейших примеров изучались системы с матрицами коэффициентов 2-го порядка. Случай двух переменных помимо простоты привлекателен еще и тем, что позволяет придать решению системы наглядную геометрическую интерпретацию. Теперь мы знаем, что два линейных уравнения системы с двумя переменными задают на плоскости две прямые, которые по своему взаимному расположению могут характеризоваться как пересекающиеся, накладывающиеся друг на друга и параллельные.

В случае пересечения прямых существует единственная общая для них точка – точка пересечения, координаты которой и являются искомыми величинами. Это означает, что решение существует и единственно, т.е. система уравнений – совместная и определенная.

В случае наложения прямых имеется бесконечно большое количество общих точек, что свидетельствует о наличии бесконечного множества решений. Такая система  совместная, но неопределенная.

В случае параллельности прямых общих точек у них нет, что означает отсутствие решения системы, т.е. ее несовместность.

В качестве примера произведем соответствующие геометрические построения для следующих систем.

Прямые, задаваемые этими уравнениями, построены по двум точкам их пересечения с осями координат. Для прямой , полагая одну из переменных равной нулю, имеем: {x  0, y  2}, {x  4, y  0}; для получаем:,. Координаты точки пересечения прямых являются решением системы соответствующей системы линейных уравнений.

Получение единичной матрицы в левой секции расширенной матрицы

обеспечивает единственность решения задачи.

Полученные результаты свидетельствуют об универсальности метода Гаусса в части вычисления решения систем линейных уравнений и выявления случаев неединственности решения или его отсутствия вообще.

Линейное программирование

1. Решить геометрическим способом задачу:

L() =⟶ min ,

Вершины многогранника допустимых решений найдены как точки пересечения прямых, уравнения которых получены преобразованием неравенств системы условий в равенства. Подсчитаем значения целевой функции в вершинах, координаты которых легко определяются по рисунку как пересечения соответствующих прямых: L()=12, L()=16, L()=64, L()=22. Отсюда следует, что оптимальное решение:= 1.5,= 12.

2. Решить симплекс-методом задачу:

L() =⟶ mах ,

Введением балансовых переменных инеравенства задачи преобразуются в систему равенств и условий неотрицательности переменных

Выберем в качестве базисных переменных первые три, т.е. выразим их через свободные переменные ,,. Стрелки указывают, что сначала выражениеиз второго уравнения подставляется в первое и третье уравнения, а, затем, с помощью первого уравненияисключается из последнего уравнения и, тем самым, обеспечивается выражение базисных переменных только через свободные.

L= 30 + .

Полагая свободные переменные равными 0, находим начальное допустимое решение =(15, 5, 18, 0, 0, 0),=30.

Первая итерация. Увеличение значения L возможно только за счет роста переменной при=0,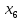=0. Первое и третье равенства допускают неограниченный рост. Однако второе равенство при условии неотрицательности переменнойв качестве максимально допустимого значения разрешает лишь=5/2. Тогда следующее допустимое решение

=(20, 0, 28, 2.5, 0, 0), =75/2=37.5 .

Вторая итерация. Теперь в качестве базисных переменных примем

L= 37.5  1.5 0.5.

Поскольку коэффициенты целевой функции при свободных переменных отрицательны, то её дальнейшее увеличение невозможно и решением задачи является предыдущее допустимое решение

= 28, =2.5,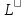=37.5.

3. Решить симплекс-методом задачу:

L(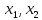) =⟶ min ,

За счет ввода балансовых переменных ,,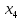ограничения задачи преобразуются в систему равенств с равноправными переменными

Выберем переменные ,,в качестве базисных и выразим их через свободные переменныеи, т.е. приведем систему ограничений задачи к виду

Выразим целевую функцию через свободные переменные

L() =+.

Полагая ==0, найдем=0.5,=1.5,=2.5 и получим начальное допустимое решение=(0, 0.5, 0, 1.5, 2.5),=0.5.

Первая итерация. Уменьшение L возможно только за счет роста . Увеличение этой переменной лимитируют второе и третье равенства. Из условия равенстваинулю, сохраняя=0, находим соответственно=3 и=5 и, выбирая наименьшее из них, получаем первое допустимое решение=(0, 2, 3, 0, 1),=2. Теперь в качестве свободных переменных выберем те, которые в базисе имеют нулевые координаты. Второе уравнение позволяет выразить базисную переменнуючерез свободные переменныеи. Тогда, подставляя полученное выражение дляв остальные уравнения, найдем

L()=2  +.

Вторая итерация. Уменьшить величину L может только . Два первых уравнения не ограничивают ее рост. Удерживая=0 в третьем равенстве и обеспечивая неотрицательность, найдем максимально допустимое значение=0.2 Подсчитав величины остальных переменных, получим=(0.2, 2.4, 3.6, 0, 0),=2.2. Взяв свободными переменными ипреобразуем два последних уравнения, исключив из них.

L()=2.2 + 0.8+ 0.2.

Коэффициенты целевой функции при переменных положительны. Поэтому ее дальнейшее уменьшение невозможно, и тогда решение задачи

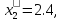
= 2.2.

Задачи для самостоятельного решения

1. Найти матрицу С = A + 3B, где A = , B =.

2. Вычислить произведение матриц AB и BA для

А = и В =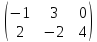

3. Найти решение систем линейных уравнений

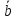4. Определить косинус угла между векторами = (1, 2) и= (1,1) .

5. Дано: =2,=3 и . Вычислить скалярное произведение

(5+ 3)(2).

6. Решить системы линейных уравнений и сопроводить геометрической интерпретацией:

7. Первую задачу практикума из раздела ЛП решить симплекс-методом.

8. Вторую и третью задачи решить геометрическим способом.

9. Проверить оптимальность решения задачи п.5.7, следуя изложенной

там схеме.

Вопросы для самопроверки

1. Определение матрицы. Классификация матриц по внешнему признаку (прямоугольная, квадратная, вектор-строка, вектор-столбец, число) и внутреннему содержанию (треугольная, диагональная, единичная, нулевая). Операции над матрицами: равенство матриц, сумма матриц, умножение матрицы на число и на другую матрицу. Примеры практического применения матричной алгебры.

2. Определение системы линейных уравнений и ее решения. Совместность, неопределенность, несовместность. Расширенная матрица. Метод Гаусса. Элементарные преобразования. Балансовая модель Леонтьева.

3. Понятие вектора, модуль вектора. Равенство векторов. Сложение векторов, умножение вектора на число, скалярное произведение векторов. Геометрия операций над векторами. Аналитические признаки коллинеарности и ортогональности векторов. Базис, декартова система координат. Реализация операций над векторами в координатах.

4. Аналитический и геометрический способы задания линии, их эквивалентность. Точка и направляющий вектор как идентификаторы прямой. Уравнения прямой линии (векторное, параметрические, каноническое, общее). Задачи о прямых: выявление особенностей прямой по ее уравнению; построение уравнения прямой, проходящей через заданную точку параллельно и перпендикулярно заданному направлению (прямой линии); нахождение уравнения прямой, проходящей через две заданные точки; вычисление точки пересечения двух прямых; выявление параллельности и наложения прямых; геометрическая интерпретация решения системы двух уравнений с двумя неизвестными.

5. Формулировка оптимизационной задачи, ее формализация в рамках линейного программирования и частные постановки (общая, дробно-линейная, транспортная). Целевая функция задачи линейного программирования, критерий оптимальности, система ограничений. Многогранник допустимых решений, оптимальное решение. Геометрический способ решения задачи ЛП. Алгоритмическая основа симплекс-метода. Разновидности математического программирования (целочисленное, нелинейное, динамическое).

Контрольные

Контрольная 1

1. Вычислить  3.

2. Перемножить матрицы .

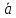
3. = (1,–1), = (0, 1),+= ?= ? Проверить‖ ,⊥ .

4. Решить СЛУ и дать геометрическую интерпретацию

5. Построить уравнения прямых и :

= (1, 1) ∊ ⊥ = (1,–3); ∊ ‖ .

Контрольная 2 (внеаудиторная)

Задачи ЛП решить геометрически и симплекс-методом:

L() =⟶ min, L() =⟶ max ,

Ч А С Т Ь 2

Т Е О Р И Я В Е Р О Я Т Н О С Т Е Й