3. Статистический анализ результатов экспериментов

Под статистикой здесь и далее будет подразумеваться регистрация конкретных результатов различных случайных явлений и экспериментов.

Рассмотрим более детально эксперимент с бросанием монеты n раз. Результат каждого отдельного испытания очевидно непредсказуем и имеет всего два исхода ‘’орел’’ или ’’решка’’. Обозначим символом m количество выпадений орла в результате эксперимента. Число m называется частотой данного случайного события, а величина р=  его относительной частотой. Реально проводимый эксперимент с неизбежностью убеждает, что относительная частота выпадений орла с увеличением числа испытаний стабилизируется около 1/2 , т.е. примерно в половине испытаний выпадает орел и величина эта тем ближе к 0,5 чем больше количество испытаний. На изображенном ниже рисунке принцип

стабилизации относительной частоты реализуется как размещение ее графика при наличии хаотичности в канале между двумя кривыми, асимптотически приближающимися к горизонтальной прямой р=0,5 .

Для большей наглядности дискретный график изображен непрерывным.

Подводя вышеизложенному итог, зафиксируем основные особенности случайного эксперимента:

- непредсказуемость исхода отдельного испытания;

- возможность неограниченного повторения испытаний в

одинаковых условиях;

- стабилизация относительной частоты случайного события с

увеличением количества испытаний.

Величина, около которой происходит стабилизация относительной частоты случайного события как раз и характеризует его вероятность. Нередко в свой речи мы выражаем интуитивное понимание вероятности реализации той или иной ситуации формулировками типа “шансы пятьдесят на пятьдесят” или “девять против одного”. Теория вероятностей поднимает тему случайности до уровня серьезной и строгой науки.

4. Множество событий и операции на нем

В каждом конкретном случайном эксперименте случайные события образуют множество, на котором могут быть введены различные операции, позволяющие из простейших событий формировать сложные события. В дальнейшем, следуя традиции, случайные события как элементы соответствующего множества будут обозначаться прописными латинскими буквами, а когда это будет удобно, то и русскими. Словесное описание содержания события раскрывается с помощью знака равенства, который в данной ситуации читается как “состоит в том, что”. Например, запись А=“выпал орел” может быть прочитана как написано и означает, что содержанием события А является выпадение орла при бросании монеты.

Первой в списке операций логично поставить сравнение событий. Если событие В происходит всегда, когда произошло событие А, то говорят что из А следует В и обозначают символом АÌВ.

Например, если при бросании кубика А=”выпала цифра 2’’ и В=”выпало четное число”, то АÌВ. Однако в данной ситуации очевидно из В не следует А, т.е. ВËА. Таким образом все случайные события относительно друг друга находятся в отношении следствия с ответом “да” или “нет”.

Теперь можно сформулировать условие равенства событий.

События А и В называются равными, если из А следует В и наоборот, т.е. АÌВ и ВÌА Û А=В. Например, если при бросании кубика А=”выпало четное число”, а В=”выпало или 2 или 4 или 6”, то А=В.

Суммой двух событий называется событие А+В, которое состоит в том, что произошло событие или А или В или оба одновременно. Здесь “одновременно” не просто слово, а термин, понимаемый не буквально как реализация событий физически в один момент времени, а в смысле “вместе”. В этом определении “или” имеет не исключающий характер, поскольку допускает совместное возникновение событий. Если в эксперименте со стрельбой =”попасть в мишень в первом выстреле”, а=”попасть в мишень во втором выстреле”, то+=”попасть или в первом выстреле или во втором выстреле или попасть одновременно в первом и втором выстреле, т.е. дважды”. Здесь рассматривается одновременное (в смысле вместе) попадание в двух выстрелах, хотя одновременно произвести два выстрела из одного и того же оружия физически невозможно. Смысловое содержание суммы событий в данном случае может быть раскрыто так: “в серии из двух выстрелов попасть хотя бы один раз”.

Применение к случайным событиям символики теории множеств объясняется глубоким идейным сходством таких объектов как множества и случайные события. Поэтому аналогично теории множеств в теории вероятностей операции над случайными событиями иллюстрируются кругами Эйлера. Сумма событий является аналогом объединения множеств и обозначается соответственно как заштрихованная область.

Из определения суммы событий следует, что она обладает свойствами коммутативности (перестановочности слагаемых)

А+В=В+А

и ассоциативности (возможности изменения порядка суммирования)

А+(В+С)=(А+В)+С.

Очевидно, что АÌА+В "В, а также А+А=А. Последний результат свидетельствует о принципиальном отличии алгебры событий от привычной алгебры чисел.

Упражнение. При бросании кубика представить случайное событие А=”выпало четное число” в виде суммы событий его составляющих, введя соответствующие обозначения.

Произведением двух событий А и В называется событие А×В или просто АВ, которое заключается в том, что события А и В произошли одновременно. Геометрическая интерпретация этой операции выглядит аналогично пересечению множеств как общая часть обоих эллипсов. Применительно к задаче о двух выстрелах по мишени при обозначении = “попадание в первом выстреле”, а=”попадание во втором выстреле” попадание дважды будет являться произведением этих событий, т.е.=”попасть дважды”.

В соответствии содержанием операции произведения событий

АА=А.

Умножение событий коммутативно (сомножители можно менять местами)

АВ= ВА,

ассоциативно (сомножители можно группировать в указанном порядке)

А(ВС)=(АВ)С

и дистрибутивно (можно раскрывать скобки и выносить общий множитель за скобки)

А(В+С)=АВ+АС.

Скобки, как и обычно, устанавливают приоритет операций.

Рассмотренные операции над событиями в частности имеют своими следствиями: АÉ АВÌВ, А+АВ=А при любом В как сумма события фактически с самим собой, в чем нетрудно убедиться с помощью кругов Эйлера. Особенности алгебры событий проявляются в таком примере

(А+В)(А+С)=АА+АС+ВА+ВС=(А+АВ)+АС+ВС=А+АС+ВС=(А+АС)+ВС=А+ВС.

Упражнение. Доказать полученный результат непосредственно с помощью кругов Эйлера для всех трех событий А, В и С.

Основное назначение операций над событиями - формирование из простых событий более сложных.

Примеры.

1. В серии из пяти выстрелов по мишени событие С=”не менее 3-х попаданий” представимо в виде суммы событий С=, где=”ровно ‘к’ попаданий”.

2. При одновременном бросании двух кубиков событие С=”сумма выпавших цифр четна” реализуется в случае четности или нечетности обеих цифр. Введем в рассмотрение события =”на𝑖-м кубике выпало четное число”, =”на𝑖-м кубике выпало нечетное число” и образуем из них событие С= .

Событие называется противоположным событию А, если оно состоит в том, что А не произошло (А=”выпал орел” Û =”выпала решка”).

Событие Ω называется достоверным, если оно происходит всегда (“выпал орел или решка”=Ω).

Событие ∅ называется невозможным, если оно не происходит никогда (“выпал орел и решка”=∅).

События А и В называются несовместными, если они не могут произойти одновременно (в смысле вместе, а не физически в один момент времени). Для несовместных событий А и В очевидно АВ=∅, т.е. произведение двух несовместных событий - невозможное событие.

Событие (исход) называется элементарным, если оно непредставимо в виде комбинации других событий.

События образуют полный набор, если они все попарно несовместны, т.е. =∅ при " 𝑖≠𝑗, а их сумма - достоверное событие =Ω . В примере с бросанием кубика, обозначив =”выпала цифра ‘𝑖’ ”, получаем шесть попарно несовместных элементарных событий, которые в своей сумме очевидно дают достоверное событие. Таким образом события , образуют полный набор элементарных исходов и любое сложное событие будет представлять собой их некоторую комбинацию. Из вышеизложенного следует, что =∅, =Ω, А+=Ω, А=∅ ввиду несовместности события с ему противоположным, т.е. событие и ему противоположное образуют полный набор.

5. Эмпирическая вероятность

Здесь речь пойдет о статистическом подходе к расчету вероятностей на основе анализа результатов случайного эксперимента. Полученные данные о частоте исходов различных случайных событий в ходе СЭ позволяют сделать определенные выводы о шансах их реализации. Шанс случайного события резонно считать тем выше, чем больше частота его возникновения. Таким образом, шанс случайного события произойти в будущем приходится оценивать по результатам эксперимента в прошлом.

Эмпирическая вероятность события А принимается равной его относительной частоте в эксперименте из 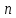испытаний

(А)= ,

где (А)- количество исходов события А.

К очевидным свойствам эмпирической вероятности относятся:

1. 0£(А)£1, при этом 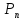(∅)=0, 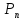(Ω)=1 (=0,=1).

2. Для несовместных событий

(А+В)= = = + = (А)+(В).

3. Для полного набора событий в силу их несовместности

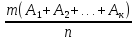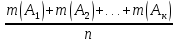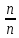()=== =1.

Общепринятое понимание вероятности заключается в оценке шанса события произойти в будущем. Эмпирическая вероятность этому условию явно не удовлетворяет. Она предполагает реальное проведение эксперимента, о чем свидетельствует индекс n, означающий количество испытаний. В ее названии звучат два совершенно разноплановых фактора - эмпирика в виде количества зафиксированных реализаций события в ходе эксперимента (однозначное прошлое) и вероятность события еще только произойти (ожидаемое будущее). Главное назначение эмпирической вероятности состоит в том, что она подводит к обоснованию метода расчета “полновесной” вероятности и выявлению свойств, которыми та с необходимостью должна обладать. Кроме того, рассмотренные выше обстоятельства наводят на мысль, что находясь на статистических позициях за вероятность события А разумно принять предел относительной частоты этого события при неограниченном увеличении числа испытаний, т.е.

Р(А) = .

Однако такой подход неконструктивен, поскольку предполагается реальное повторение эксперимента в неограниченном количестве, и построить на этой основе математический аппарат расчета вероятностей случайных событий не представляется возможным.

6. Классическая вероятность

В процедурах принятия решений, а мы всю свою жизнь постоянно этим занимаемся, важнейшую роль играет анализ вероятностного расклада позитивных и негативных последствий планируемых действий и мероприятий, будь то расчет разумных затрат на рекламную компанию или оценка характера и размера ставок в казино. В отличие от эмпирической вероятности практический интерес в этой сфере человеческой деятельности может представлять только такая вероятность, которая является числовой характеристикой возможности появления случайного события, определяемая до опыта (априорная вероятность). В самом деле, мало радости подсчитывать убытки , вместо того, чтобы грамотно спрогнозировать ситуацию и предусмотрительно не совершить ошибочные действия.

Этим целям служит классическая вероятность, требующая введения некоторых вспомогательных понятий. Как и ранее предполагается, что случайный эксперимент может быть воспроизведен неограниченное количество раз в одинаковых условиях. Однако принципиальным моментом при расчете классической вероятности является то, что эксперимент производится чисто умозрительно. Исход эксперимента называется благоприятным для события А, если оно следует из такого исхода. Например, при бросании кубика для события А=”выпало четное число” из 6 возможных благоприятны три исхода “2”, ”4”, ”6”. Таким образом, случайное событие может быть описано перечнем благоприятных исходов. В нашем случае ”выпало четное число” =”выпало 2 или 4 или 6”.

Исходы с одинаковыми шансами на реализацию называются равновозможными. В примере с кубиком таковыми являются все шесть мыслимых исходов.

Теперь рассмотрим мысленный эксперимент с N равновозможными и несовместными исходами. Вероятностью Р(А) случайного события А называется отношение числа (А) благоприятных исходов для А к общему числуN равновозможных несовместных исходов

Р (А)= .

Это равенство представляет собой определение классической вероятности, которая вычисляется как доля благоприятных исходов в общем количестве возможных исходов. Классическая вероятность в отличие от эмпирической не требует проведения экспериментов и в то же время обладает всеми свойствами последней. В самом деле, из классического определения вероятности следует:

1. 0£Р (А)£1, Р(∅)=0 (нет благоприятных исходов), Р(Ω)=1 (все исходы

благоприятны).