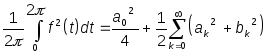Глава 1.

Ряд Фурье.

1.1 Понятие полноты и ортогональности системы функций.

Ряд Фурье как разложение по полному ортогональному базису.

Из курса линейной алгебры известно, что если в линейном пространстве конечной размерности выбрать некоторый базис, то любой элемент этого пространства может быть разложен по этому базису ( притом единственным образом) и затем характеризоваться дискретным набором чисел-коэффициентов в разложении (пример-вектор).

Этот подход берется за основу при представлении сигнала, описываемого некоторой кусочно-непрерывной функцией в виде ряда Фурье. Если в пространстве кусочно-непрерывных функций в качестве базиса рассмотреть некоторую систему ортогональных функций и разложить по нему f(t), то исходный сигнал можно задавать числовой последовательностью, состоящей из коэффициентов разложения .

Итак, рассмотрим пространство кусочно-непрерывных на отрезке длиной Т функций. Под кусочно-непрерывной функцией на сегменте длиной Т будем понимать такую функцию, которая непрерывна на нем всюду, за исключением конечного числа точек, в которых она имеет разрыв первого рода. Скалярное произведение двух любых функций f(t) и g(t) этого пространства определим следующим образом:

Определим норму элемента f как .

Множество функций называется ортогональным на интервале длиной Т, если входящие в эту систему функции попарно ортогональны, т.е.

(1).

При множество называется ортонормированным.

Назовем рядом Фурье функции f(t) по ортогональной системе функций ряд вида

(2)

где есть постоянные числа, называемые коэффициентами Фурье функции f(t) и определяемые равенствами

(3)

Естественно назвать конечную сумму N-ой частичной суммой ряда Фурье.

Ортогональное множество функций , удовлетворяющее условию, называется полным, если для любого кусочно-непрерывного сигнала с конечной мощностью, т.е.

и и ,соответственно, конечная сумма

, такая что .

Таким образом, основная идея представления сигнала в виде ряда Фурье состоит в том, что непрерывная функция f(t) заменяется числовой последовательностью . При этом , если система является полной , f(t) может быть представлена с любой степенью точности в виде конечного разложения т.е. конечного набора чисел.

Важнейшим примером ортогональной системы является тригонометрическая система функций на интервале .

Отдельно системы состоящие из косинусов

и только из синусов будут ортогональны на интервале .

Кроме синусоидальных систем функций при обработке сигналов используется ряд систем функций несинусоидального вида, состоящие из прямоугольных и квадратных волн.

1.2 Тригонометрический ряд Фурье.

В качестве иллюстрации общего метода ортогональных представлений рассмотрим тригонометрическую систему функций:

на интервале .

Для того, чтобы доказать, что эта система действительно ортогональна, необходимо вывести три следующих интеграла:

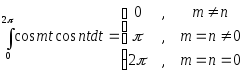
(5)

Но эта система не является ортонормированной.

Чтобы привести систему к нормальному виду, нужно поделить все функции системы на их норму. Это для и для остальных .

Разложение f(t) в ряд типа (2) будет иметь вид:

(6)

Чтобы получить выражение для коэффициентов , умножим обе части (6) на и проинтегрируем ряд почленно на интервале .Отметим, что такую процедуру можно провести не для любого функционального ряда. Каким условиям для этого должна удовлетворять функция f(t), сформулируем ниже.

В результате, используя свойство ортогональности, получим

(7)

Для получения умножим обе части уравнения (6) на и проинтегируем в тех же пределах.

(8).

Коэффициенты называются коэффициентами Фурье, а тригонометрический ряд (6) с такими коэффициентами рядом Фурье.

До сих пор мы писали формальное разложение функций в ряд Фурье без исследования вопроса сходимости построенного ряда. На этот вопрос отвечают приводимые без доказательства теоремы:

Если периодическая функция f(t) c периодом 2p кусочно-монотонна и ограничена на отрезке , то ряд Фурье, построенный для этой функции, сходится во всех точках . При этом сумма полученного ряда равна значению функции f(t) в точках непрерывности. В точках разрыва функции f(t) сумма ряда равняется среднему арифметическому пределов функции справа и слева, т.е. если с-точка разрыва функции, то сумма ряда в этой точке равна [f(c-0)+f(c+0]/2.

Если периодическая функция f(t) c периодом 2p непрерывна на всей действительной оси и имеет кусочно-непрерывную производную на периоде, то ее ряд Фурье сходится к ней равномерно.

Примем без доказательства тот факт, что тригонометрическая система на интервале длиной 2p является полной. Тогда в силу (3) любая кусочно- непрерывная ограниченная на этом интервале функция может быть приближена частичной суммой ряда Фурье в смысле среднеквадратичного.

Отметим одно важное свойство периодических функций , состоящее в том, что при вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования промежутком интегрирования , где l-любое число. Это свойство легко доказывается непосредственной соответствующей заменой переменной при интегрировании и в некоторых случаях упрощает процесс нахождения коэффициентов.

Для иллюстрации разложим в ряд Фурье следующую периодическую функцию .

Эта функция называется прямоугольной волной и играет важную роль в теории фильтров.

В данном случае коэффициенты Фурье удобно находить путем интегрирования по промежутку .

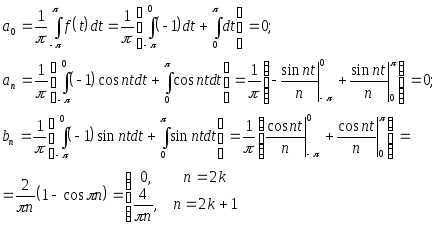Таким образом, получаем искомое разложение

(9).

Из выражений для коэффициентов Фурье (7,8) следует, что для нечетной функции все коэффициенты =0, а для нечетной-

Поэтому в разобранном примере коэффициенты можно было без вычисления положить равными нулю.

Рассмотрим вопрос разложения в ряд Фурье периодической функции f(t) с периодом 2l отличным от 2p. Разложим ее в ряд Фурье , предварительно сделав замену переменной t=lx/p. Тогда функция f(lx/p) как функция от x будет иметь период 2p и, следовательно, ее можно разложить в ряд Фурье на отрезке -p<x<p

по формулам (6-8).

(10)

где

Возвращаясь теперь к исходной переменной t=lx/p,получим:

(11),

Ряд Фурье (10) окончательно будет иметь вид

(12),

где коэффициенты определяются по формулам (11).

Это и есть ряд Фурье для функции периодической с периодом 2l.

В ряд Фурье можно разложить любую кусочно-монотонную функцию с ограниченным интервалом изменения независимой переменной. Для этого нужно продолжить периодическим образом данную функцию на всю числовую ось и разложить полученную периодическую функцию в ряд Фурье. Сумма этого ряда будет совпадать с заданной функцией в точках ее непрерывности.

Отметим, что если функция задана на промежутке (0,l), то ее можно периодически продолжить четным образом с периодом 2l, нечетным образом с периодом 2l или так, что функция будет периодической с периодом, но не симметричной относительно 0. В каждом из этих случаев ряд Фурье будет содержать только синусы, только косинусы, синусы и косинусы.

Таким образом любая периодическая функция или функция с ограниченным интервалом изменения независимой переменной может быть разложена на отдельные гармонические колебания. Сам процесс разложения периодической функции по гармоникам называют гармоническим анализом.

1.3 Равенство Парсеваля.

Чтобы понять физический смысл такого разложения , возведем обе части (12) в квадрат и проинтегрирум обе части по периоду Т. Учитывая свойство ортогональности (5), получим равенство,

(13),

которое составляет содержание теоремы Парсеваля.

есть средняя мощность сигнала, а множество чисел

дает распределение мощности в сигнале f(t) по частотам.

1.4 Ряд Фурье как наилучшее среднеквадратичное приближение.

Представление функции бесконечным рядом (Фурье, Тейлора и т.д. )имеет на практике тот смысл, что конечная сумма, получающаяся при обрывании ряда на n-ом члене, является приближенным выражением разлагаемой функции. Это приближенное выражение можно довести до сколь угодной степени точности путем выбора достаточно большого значения n. Однако характер приближенного представления может быть различным. Так ,например, сумма первых n членов ряда Тейлора совпадает с рассматриваемой функцией в одной точке и в этой точке имеет производные до n-го порядка, совпадающие с производными рассматриваемой функции. Полином Лагранжа n-ой степени совпадает с рассматриваемой функцией в n+1точках. Покажем, что ряд Фурье обеспечивает наилучшее приближение данной функции в среднем, т.е. что среди всех тригонометрических полонизмов порядка n наименьшее среднеквадратичное уклонение от функции f(t) имеет тот многочлен, коэффициенты которого есть коэффициенты Фурье функции f(t).

Пусть дана периодическая с периодом 2p функция f(t). Среди всех тригонометрических многочленов n-го порядка

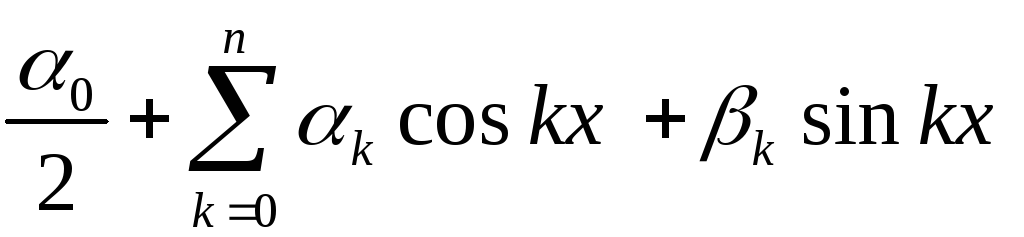
требуется найти путем подбора коэффициентов тот многочлен, для которого среднеквадратичное уклонение, определяемое равенством

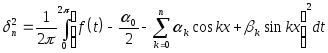(13)

было бы минимальным.

Используя свойство ортогональности тригонометрической системы (5), а также выражения для коэффициентов (7),(8), получаем:

Прибавляя и вычитая сумму 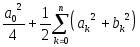,будем иметь

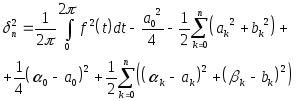(14).

Это выражение, очевидно, достигает минимального значения при . Таким образом, среднеквадратичное уклонение тригонометрического полинома от функции f(t) будет наименьшим тогда, когда его коэффициенты есть коэффициенты Фурье.

Величина наименьшего среднеквадратичного отклонения равна

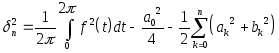(15).

Т.к. при любом n , имеем

(16).

Это неравенство называется неравенством Бесселя.

Для полной системы, какой является тригонометрическая система на [0,2p] при n®¥. Таким образом

Отсюда следует равенство Парсеваля (13):