лекции / LEKKURS4

Глава 4.

ДИСКРЕТИЗАЦИЯ. ЭФФЕКТ НАЛОЖЕНИЯ ЧАСТОТ. ТЕОРЕМА ОТСЧЕТОВ.

4.1 Математическое представление процесса дискретизации.

Непрерывные сигналы, поступающие с выхода измерительных устройств, как правило не обрабатываются непосредственно, а подвергаются дискретизации, т.е. наблюдаются только в определенные моменты времени. Поэтому важно понять , как последовательности, полученные таким образом, связаны с исходным сигналом, каковы правила дискретизации, как по временной выборке восстановить исходный сигнал.

Рассмотрим непрерывный (аналоговый) сигнал x(t) , имеющий преобразование Фурье X(n):

(1)

(2)

Говорят, что последовательность x(n) со значениями x(n)=x(nT) из x(t) периодической дискретизацией, параметр Т при этом называют временным периодом дискретизации. Величина, обратная Т (обозначим ее за ), т.е. , называется частотой дискретизации.

Чтобы определить , в каком смысле дискретизованный сигнал x(n) представляет исходный сигнал x(t), найдем связь между их преобразованиями Фурье. Преобразование Фурье непрерывного сигнала дается формулой (1). Найдем выражение для преобразования Фурье дискретизованного сигнала.

Прежде всего найдем математическое выражение процесса дискретизации функции x(t). Для этого рассмотрим процесс дискретизации как умножение функции x(t) на сумму импульсов Дирака, разделенных промежутками 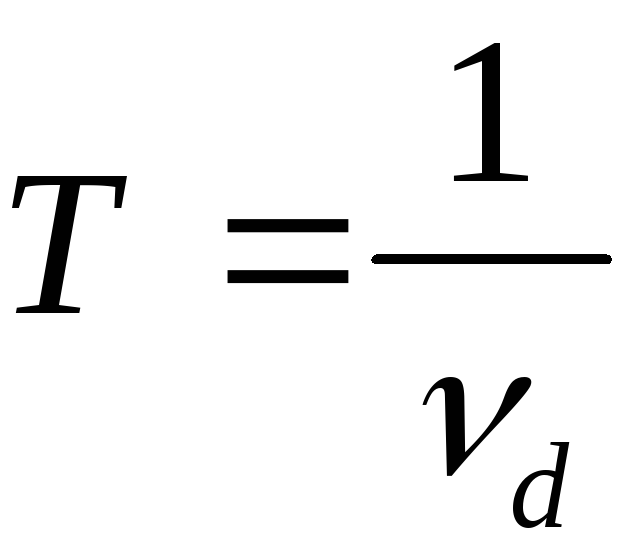с интенсивностью Т. Такую сумму импульсов можно представить как гребневую функцию. Поэтому дискретизованный сигнал имеет вид:

(3).

Справедливость такого представления можно обосновать тем, что при уменьшении временного интервала дискретизации в этом выражении имеет место предельный переход к исходной непрерывной функции x(t).

Действительно переходя при Т®0 от суммирования по n (т.е. по дискретным моментам времени nT) к интегрированию по непрерывной временной переменной и используя определение d-функции, получим

(4).

При этом дискретные моменты времени обозначены новой переменной с индексом , временной период дискретизации .

Сделаем важное для дальнейшего предположение о том, что сигнал x(t) имеет ограниченную полосу частот, т.е. его образ Фурье X(n) равен нулю вне некоторого интервала.

4.2 Преобразование Фурье в дискретном времени.

Теперь перейдем непосредственно к нахождению преобразования Фурье дискретизованного сигнала.

Будем обозначать искомый Фурье-образ дискретизованного сигнала как . Пользуясь определением преобразования Фурье (1) и выражением для (3) , имеем:

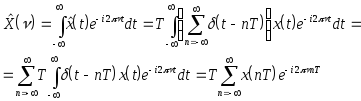
При этом мы поменяли местами порядок суммирования и интегрирования и воспользовались определением d-функции.

Таким образом, мы получили, что преобразование Фурье дискретизованой последовательности имеет вид:

(5),

где мы использовали обозначение x(n)=x(nT).

Обратное преобразование Фурье дискретизованного сигнала можно получить, используя свойство ортогональности экспонент на периоде 1/T. для этого умножим правую и левую части (5) на

и проинтегрируем поинтервалу длиной 1/T.

Откуда

(6)

Формулы (5) и (6) представляют собой преобразование Фурье в дискретном времени.

4.3 Связь между образами Фурье непрерывного и дискретизованного сигнала.

Прежде чем искать связь между образами Фурье непрерывного и дискретизованного сигналов, сделаем несколько замечаний относительно . Как следует из выражения (5), преобразование Фурье дискретизованной последовательности есть непрерывная функция частоты и является периодической функцией.

Кроме того, является периодической функцией n с периодом 1/T в силу периодических свойств синусов и косинусов .

Выясним его вид более конкретно. Рассматривая значения временной последовательности в точках n как значения непрерывного сигнала в дискретные моменты времени nT, а также используя определение (2) обратного преобразования Фурье для непрерывного сигнала, получим:

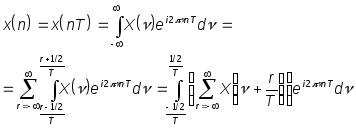(7).

При этом мы представавили интеграл в бесконечных пределах как сумму бесконечного числа интегралов по интервалом длиной 1/T. Заменой переменной 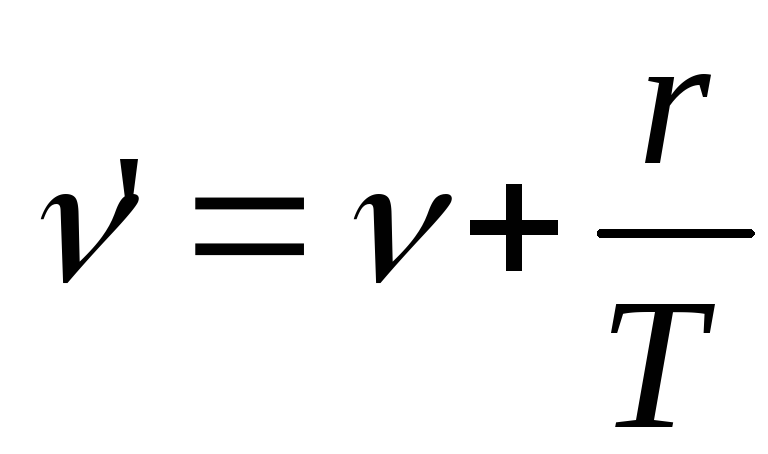свели каждый член суммы к интегрированию в пределах от до . Далее изменили порядок суммирования и интегрирования и учли тот факт, что

при целых значениях r и n. Сравнивая (6) и (7), получим связь между преобразлванием Фурье непрерывного и дискретизованного сигналов:

(8).

Таким образом, спектр дискретизованного сигнала получается периодическим продолжением спектра непрерывного сигнала на всю частотную ось с периодом, равным частоте дискретизации .

4.4 Эффект наложения частот.Теорема дискретизации.

Может оказаться, что временной период дискретизации выбран настолько велик, что частотный период дискретизации окажется меньше ширины спектра исходного сигнала. В этом случае сдвинутые варианты спектра будут перекрываться и верхние частоты непрерывного сигнала будут отражаться в более низкие частоты в дискретизованном сигнале. Это явление, при котором высокочастотные компоненты спектра сигнала отождествляются с более низкими частотами, носит название явления наложения или подмены частот.

Условия, налагаемые на частоту дискретизации, позволяющие избежать этого явления, и составляет содержание теоремы дискретизации:

Пусть функция x(t) удовлетворяет следующим условиям:

1. x(t) определена при -¥<t<¥;

2. Существует преобразование Фурье X(n) функции x(t);

3. Функция X(n) ограничена по частоте т.е.

Для того, чтобы периодическое повторение спектра, вызванное дискретизацией сигнала, не изменяла повторяемый спектр, необходимо и достаточно выполнение неравенства

или

Здесь -максимальная частота спектра исходного сигнала.

Частота , играющая определяющую роль в процессе дискретизации сигнала, называют частотой Найквиста.

4.5 Теорема отсчетов (Котельникова).

Перейдем к рассмотрению возможности восстановления исходной непрерывной функции, если известны ее значения только в дискретные моменты времени. Фундаментальный результат, который утверждает , что это возможно, называется теоремой отсчетов ( в отечественной литературе теоремой Котельникова):

Пусть функция x(t) удовлетворяет условиям предыдущей теоремы дискретизации, т.е.

1. x(t) определена при -¥<t<¥;

2. Существует преобразование Фурье X(n) функции x(t);

3. Функция X(n) ограничена по частоте т.е.

Тогда, если частота дискретизации удовлетворяет теореме дискретизации, т.е. , то функция x(t) может быть однозначно восстановлена по дискретным значениям x(nT).

Доказательство:

Т.к. спектр дискретизованного сигнала получается периодическим продолжением с периодом спектра исходного сигнала, то наоборот, ограниченный спектр непрерывного сигнала можно получить из спектра временной последовательности, “вырезая” его умножением на прямоугольную функцию:

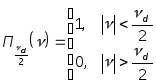
Таким образом,

Исходный сигнал x(t) можно найти, воспользовавшись обратным преобразованием Фурье:

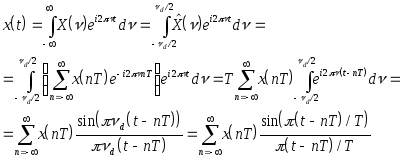(11)

Выражение (9) дает интерполяционную формулу для восстановления непрерывного сигнала x(t) по последовательности дискретных его значений. Т.к. значение интерполяционного полинома при t=nT равно единице, то в этих точках выражение (9) дает точное значение исходного непрерывного сигнала x(t).

В промежуточных точках это выражение служит интерполяционной схемой.

Отметим, что выражение (9) можно рассматривать как разложение сигнала в непрерывном времени в ряд вида

.

Рассмотрим пример, демонстрирующий эффект наложения частот. Покажем, что если выборка значений синусоиды с частотой n производится с временным интервалом Т, большим чем, то такую выборку можно перепутать с выборкой синусоиды меньшей частоты. Наряду с истинной частотой в выборке появится и другая меньшая частота- частота подмены.

Итак, рассмотрим синусоиды . Запишем ее частоту в виде . Спектр синусоиды содержит только одну частоту n, поэтому ее и будем рассматривать как . Но вопреки требованию теоремы дискретизации возьмем временной интервал дискретизации т.е. . Выделим в этом выражении целую часть m и дробную часть q (большую нуля). Таким образом, частоту синусоиду можем записать в виде . Заменив t дискретным набором nT, получим:

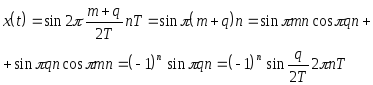
В случае четного m имеем:

Т.е. получим, что выборка синусоиды с частотой не различается с выборкой синусоиды с частотой .

В случае нечетного m

Т.е. выборка синусоиды с частотой не различается с выборкой синусоиды с частотой .

Например, пусть мы дискретизуем синусоиду с частотой n=1025 Гц с временным интервалом T=0.005. Тогда согласно сказанному выше, т.к. =100, p=10,q=0.25.

Получим, что выборка синусоиды с частотой 1025 Гц не различается с выборкой синусоиды с частотой 25 Гц. При этом такая же выборка будет и для синусоид с частотами 825,625,425,225 Гц, а также 975,775,575,375,175 Гц.

Можно нарисовать диаграмму подмены частот, если сложить гармошкой ось частот над интервалом 0-Fгц кусками по F Гц.

Если из основной частоты 1025 Гц провести перпендикуляр к основному интервалу 0-F Гц, то получится частота 25 Гц. То же значение получится и для других перечисленных частотах.

Если бы мы выбрали временной интервал дискретизации согласно теореме дискретизации, т.е. выполнили бы условие

т.е. , то целая часть m в этом случае была бы равна нулю и явления подмены частот бы не произошло. В данном случае минимальный временной интервал дискретизации, исключающий наложение частот равен