Числовые характеристики.

Знание одномерной плотности вероятности p ( x, t ) позволяет произвести статистическое усреднение как самой величины X ( t ), так и любой функции от нее. Под статистическим усреднением подразумевается усреднение по множеству ( по ансамблю реализаций ) в каком – либо сечении процесса, т. е. в фиксированный момент времени.

Для практических приложений наибольшее значение имеют следующие параметры случайного процесса: математическое ожидание, дисперсия, среднее квадратичное отклонение

Математическое ожидание служит теоретической оценкой среднего взвешенного значения случайного процесса в момент времени t:

В общем виде можно записать

где f - некоторая функция случайной величины x, имеющей плотность вероятности p_x ( x ).

Дисперсия

Дисперсия характеризует среднюю мощность отклонений случайного процесса от его среднего значения m_x ( t ). Эти отклонения называются флуктуациями.

D_x( t ) = M { [ X ( t ) - m_x(t )] ²} = M { X ² ( t ) } - m²_x ( t ) =

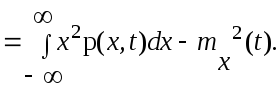
Среднее квадратичное отклонение.

Среднее квадратичное отклонение представляет собой квадратный корень из дисперсии и служит амплитудной мерой разброса значений случайного процесса в момент времени t относительно математического ожидания.

Часто дисперсию случайной величины X обозначают как σ².

В качестве примера рассмотрим часто используемый на практике закон распределения случайных величин – закон равномерного распределения. В случае равномерного распределения плотность вероятности является постоянной на некотором интервале [a, b ]. Величина этой постоянной, в соответствии с условием нормировки, должна быть равна 1/( b - a ). Тогда

p(x) = 1 / (b – a), при a ≤ x ≤ b ,

p(x) = 0 при a > x > b

Графики плотности вероятности и функции распределения случайной величины приведены ниже.

Рис. 3 Плотность вероятности (слева) и функция распределения (справа) случайной величины с равномерным распределением.

Функция распределения на интервале [a, b] линейно возрастает от 0 до 1.

F(x) = 0 при x < a,

F(x) = (x – a) / (b – a) при a ≤ x ≤ b,

F(x) = 1 при x > b .

Математическое ожидание (среднее взвешенное значение) равно середине интервала возможных значений случайной величины.

Если функция плотности вероятности имеет симметричный вид, то значение математического ожидания всегда совпадает с центром симметрии.

Для расчета дисперсии определим средний квадрат.

Отсюда по формуле дисперсии имеем

дисперсия равна одной двенадцатой квадрата ширины интервала. Среднее квадратичное значение оказывается пропорциональным этой ширине.

Нормальное распределение.

Нормальный (гауссов) закон распределения случайных величин очень удобен для анализа и особенно характерен для помех канала связи. Одномерная плотность вероятности нормальной случайной величины определяется выражением:

На рис. 4 приведен график плотности вероятности нормальной случайной величины, построенный по приведенной формуле при m_x = 0 и σ_x = 1.

Рисунок

Функция распределения для закона Гаусса не выражается через элементарные функции. В отечественной литературе принято выражать её через так называемый интеграл вероятности.

Для нормального закона с математическим ожиданием m_x и дисперсией σ_x функция распределения выражается через интеграл вероятности следующим образом:

Одномерная плотность вероятности и связанные с ней числовые характеристики позволяют получить важную информацию о свойствах случайного процесса. Однако для решения многих задач таких сведений не достаточно, так как они дают вероятностное представление о случайном процессе X(t) только в отдельные моменты времени и не определяют его изменения во времени. Для описания временных характеристик случайного процесса необходимо использовать корреляционную функцию или привлечь спектральные характеристики случайного процесса. Вспомним определение корреляционной функции из материала предыдущей лекции: корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией. В практике анализа случайных сигналов применение операции сдвига во времени позволяет получить два сечения случайного процесса в произвольные моменты времени Совокупность этих двух сечений образует двумерную случайную величину { X( t₁ ), X( t₂ )}, которая описывается двумерной плотностью вероятности p(x₁,x₂,t₁,t₂,). Когда интерес представляет флуктуационная составляющая случайного процесса, применяется корреляционная функция, представляющая собой усредненное произведение значений центрированной случайной функции X(t) – m_x(t) в моменты времени t₁ и t₂. Корреляционная функция характеризует степень статистической связи тех значений случайного процесса X(t), которые наблюдаются при t = t₁ и t =t₂. При t₁ = t₂ = t , т. е. при совмещении сечений, функция корреляции равна дисперсии.

R_x(t,t) = K_x(t,t) – m_x²(t) = Dx(t).

Рассмотрим две случайные величины X₁ и X₂. Если плотность вероятности одной случайной величины зависит от значения другой случайной величины, между этими величинами существует статистическая связь. В случае отсутствия статистической связи двумерная плотность вероятности представляет собой произведение одномерных плотностей

p(x₁,x₂) = p₁(x₁) p₂(x₂).

Данное выражение является условием статистической независимости

При наличии статистической связи между случайными величинами статистические свойства каждой из них зависят от значения, принимаемого другой случайной величиной. Связь эта может быть сильной, слабой, линейной или нелинейной. Мерой линейной статистической связи между случайными величинами является коэффициент корреляции r₁,₂.

r₁,₂ 1

Равенство коэффициента корреляции нулю свидетельствует об отсутствии линейной статистической связи между случайными величинами. При этом математическое ожидание произведения случайных величин равно произведению их математических ожиданий: M{X₁ X₂} = M{X₁}M{X₂}.

Стационарные и эргодические случайные процессы.

В общем случае вероятностные и корреляционные характеристики случайных процессов зависят от одного или нескольких моментов времени, в которые эти характеристики определяются. Вместе с тем существует класс случайных процессов, у которых зависимость характеристик от времени отсутствует. Кроме того, для некоторых случайных процессов не обязательно производить усреднение по ансамблю реализаций - можно ограничиться рассмотрением одной реализации и ее усреднением во времени.

Случайные процессы, статистические характеристики которых одинаковы во всех сечениях, называются стационарными.

Случайный процесс строго стационарен (стационарен в узком смысле), если его многомерная плотность вероятности произвольной размерности не изменяется при одновременном сдвиге всех временных сечений вдоль оси времени на одинаковую величину. Из стационарности в узком смысле следует стационарность в широком смысле, если ограничить требования тем, чтобы от временного сдвига не зависели лишь одномерная и двумерная плотности вероятности.

Для стационарного случайного процесса математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от самих моментов времени, а только от интервала между ними τ = t₂ – t₁.По этой причине при записи статистических параметров стационарного случайного процесса можно опускать обозначения фиксированных моментов времени. Корреляционная функция стационарного случайного процесса является четной R_x(-τ)=R_x(τ). Абсолютные значения корреляционной функции стационарного случайного процесса при любых сдвигах не превышают ее значения при нулевом сдвиге = 0. ! R(τ) ! R(0) = D ( Вспомним, при нулевом сдвиге значение корреляционной функции равно дисперсии случайного процесса).

Удобным для пользования является коэффициент корреляции или нормированная корреляционная функция.

r_x(τ) = R_x(τ) / D_x

Коэффициент корреляции равен единице при нулевом сдвиге, меньше или равен единице при всех остальных сдвигах, является четной функцией.

Корреляционная функция и коэффициент корреляции характеризуют связь (корреляцию) между значениями функций X(t), разделенными промежутком . Чем медленнее убывают эти функции с ростом абсолютного значения , тем больше промежуток, в течение которого наблюдается статистическая связь между мгновенными значениями случайного процесса, и тем медленнее, и более плавно изменяются его реализации во времени.

Эргодические случайные процессы.

Стационарный процесс называется эргодическим, если при определении любых его статистических характеристик усреднение по множеству (ансамблю) реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации. Кратко – среднее по ансамблю соответствует среднему по времени.

Математическое ожидание эргодического случайного процесса равно постоянной составляющей любой из его реализаций.

Дисперсия такого процесса имеет наглядный смысл мощности флуктуационной составляющей.

Достаточным условием эргодичности случайного процесса, стационарного в широком смысле, является стремление к нулю его корреляционной функции с ростом временного сдвига lim Rx(τ) = 0 при τ→∞ .

Дискретный сигнал.

Рассмотрим далее сигнал, представляющий собой некоторую последовательность символов, создаваемую дискретным источником сообщений. К. Шеннон так определяет дискретный источник сообщений: “ Можно считать, что дискретный источник создает сообщение символ за символом. Он будет выбирать последовательные символы с некоторыми вероятностями, зависящими ,вообще говоря, как от предыдущих выборов, так и от конкретного рассматриваемого символа. Физическая система или математическая модель системы, которая создает такую последовательность символов, определяемую некоторой заданной совокупностью вероятностей, называется вероятностным процессом. Поэтому можно считать, что дискретный источник представляется некоторым вероятностным процессом. Обратно, любой вероятностный процесс, который создает дискретную последовательность символов, выбираемых из некоторого конечного множества, может рассматриваться как дискретный источник”.

Статистическая структура такого процесса и статистические свойства источника вполне определяются одномерными p ( i ), двумерными p ( I, j ) вероятностями появления элементов сообщений на выходе источника. Как указывалось, если между последовательными элементами сообщения отсутствует статистическая связь, то статистическая структура сообщения полностью определяется совокупностью одномерных вероятностей. Появление того или иного элемента сообщения на выходе источника можно рассматривать как определенное событие, характеризующееся своей вероятностью появления. Для совокупности событий вместе с их априорными вероятностями появления существует понятие ансамбля.

Примерами дискретного источника могут служить:

1. Печатные тексты на различных языках.

2. Непрерывные источники сообщений, которые превращены в дискретные с помощью некоторого процесса квантования (квантованная речь, телевизионный сигнал).

3. Математические случаи, когда просто определяется абстрактно некоторый вероятностный процесс, который порождает последовательность символов.

Подобные источники создают представляют собой вероятностные процессы, известные как дискретные Марковские процессы. В общем случае результат может быть описан следующим образом. Существует конечное число возможных “состояний” системы : S₁,S₂,. . . ,S_n. Кроме того, имеется совокупность переходных вероятностей pi(j), т. е. вероятностей того, что система, находящаяся в cостоянии S_i , перейдет затем в состояние S_j. Чтобы использовать этот Марковский процесс в качестве источника сообщений, нужно только предположить, что при каждом переходе из одного состояния в другое создается одна буква. Состояния будут соответствовать “остатку влияния” предшествовавших букв.

В графическом примере “состоянием” является узловая точка схемы, а переходные вероятности и создаваемые при этом буквы указаны около соответствующих линий.

Такой источник из четырех букв A, B, C, В , имеющих, соответственно, переходные вероятности 0,1; 0,4; 0,3; 0,2, возвращаясь в узловую точку после создания очередной буквы, может формировать как конечные, так и бесконечную последовательности.

На дискретный источник можно распространить такие характеристики случайного сигнала, как эргодичность и стационарность. Полагая источник эргодическим, можно “… отождествлять средние значения вдоль некоторой последовательности со средним значением по ансамблю возможных последовательностей ( причем вероятность расхождения равна нулю)”. Например, относительная частота буквы А в частной бесконечной последовательности будет с вероятностью единица равняться ее относительной частоте по ансамблю последовательностей.

Если p_i - вероятность состояния i, а p_i ( j ) – вероятность перехода в состояние j, то, для того, чтобы процесс был стационарным, p_i должна удовлетворять условиям равновесия

p_j = p_i p_i ( j ).

В случае эргодического источника при любых начальных условиях вероятности пребывания в состоянии j после N шагов p_j (N) при N →∞ стремятся к величинам, удовлетворяющим условиям равновесия. Таким образом, дискретный источник при дальнейшем рассмотрении будет представляться случайным эргодическим стационарным процессом. Поскольку источник представляется Марковским процессом, зададимся вопросом: с какой скоростью создается последовательность? Можно ли измерять в определенном смысле этого слова, как много информации создается при этом? Материал следующих лекций будет посвящен ответу на эти вопросы.

ЛИТЕРАТУРА.

1. А. Б. Сергиенко Цифровая обработка сигналов. Изд. “Питер” 2002 г.

стр. 60 - 67.70 - 74. 127 - 128.

2. К. Шеннон Работы по теории информации и кибернетике. Изд. ИЛ М. 1963 г. стр. 251, 256 - 257.

15