Релаксационные нейронные сети

Релаксационные нейронные сети характеризуются прямым и обратным распро­странением информации между слоями нейронной сети. В основе функционирования лежит итеративный принцип работы. На каждой итерации процесса происходит обработка данных, полученных на предыдущем шаге. Такая циркуляция информации продолжается до тех пор, пока не установится состоя­ние равновесия. При этом состояния нейронных элементов перестают изменяться и ха­рактеризуются стационарными значениями. Для анализа устойчивости релаксационных нейронных сетей используются функции Ляпунова. Такие сети применяются в качестве ассоциативной памяти и для решения комбинаторных задач оптимизации. К релаксаци­онным относятся нейронные сети Хопфилда, Хэмминга, двунаправлен­ная ассоциативная память и машина Больцмана.

Нейронные сети Хопфилда

Нейронная сеть Хопфилда реализует существенное свойст­во автоассоциативной памяти - восстановление по искаженному (зашумленному) образу ближайшего к нему эталонного. Входной вектор используется как начальное состояние се­ти, и далее сеть эволюционирует согласно своей динамике. При­чем любой пример, находящийся в области притяжения хранимого образца, может быть использован как указатель для его восста­новления. Выходной (восстановленный) образец устанавливается, когда сеть достигает равновесия.

Обучение сети Хопфилда производится по правилу Хебба, методу проекций и D - проекций.

Структура сети Хопфилда (рис 2.8) состо­ит из одного слоя нейронов, число которых определяет число вхо­дов и выходов сети. Выход каждого нейрона соединен с входами всех остальных нейронов. Выходные сигналы нейронов являются одновременно входными сигналами сети: Xi(k)=Yi(k-1)

Основные зависимости, определяющие сеть Хопфилда, можно представить в виде

с начальным условием y_i(0) = x_j. В процессе функционирования сети Хопфилда можно выделить два режима: обучения и классификации. В режиме обучения на основе известных обучающих выборок х подбираются весовые коэффициенты w_ij. В режиме классификации при зафиксированных зна­чениях весов и вводе конкретного начального состояния нейронов у(0) = х возникает переходный процесс, протекающий в соответствии с выраже­нием (Формула выше) и завершающийся в одном из локальных минимумов, для которого y(k)=y(k-l).

Для безошибочной работы сети Хопфилда число запоми­наемых эталонов N не должно превышать 0,15n(n-число нейронов).

Рис. 2.8. Структура нейронной сети Хопфилда

Проблема устойчивости сети Хопфилда была решена после того, как Кохеном и Гроссбергом была доказана теорема, опреде­ляющая достаточное условие устойчивости сетей с обратными связями, а именно, сеть с обратными связями является устойчивой, если матрица ее весов симметрична (W_ij = W_ji) и имеет нули на главной диагонали (W_ii = 0).

Динамическое изменение состояний сети может быть вы­полнено, двумя способами: синхронно и асин­хронно. В первом случае все элементы модифицируются одно­временно на каждом временном шаге, во втором - в каждый мо­мент времени выбирается и подвергается обработке один эле­мент. Этот элемент может выбираться случайно.

Параллельная динамика характеризуется синхронным функ­ционированием нейронных элементов сети. При этом за один такт ра­боты сети все нейроны одновременно изменяют свое состояние:

где i = l,n.

Последовательная динамика характеризуется асинхронным про­цессом работы нейронной сети. В этом случае за один такт работы ней­ронной сети изменяется состояние только одного нейронного элемента:

Нейронная сеть Хэмминга

Нейронная сеть Хэмминга была предложена в 1987 г. Р.Липпманом. Она представляет собой релак­сационную многослойную сеть с обратными связями между отдель­ными слоями. Сеть Хэмминга применяется в качестве ассоциативной памяти. При распознавании образов она использует в качестве меры близости расстояние Хэмминга, между тестовым вектором, подаваемым на вход сети, и векторами обучающих выборок, закодированными в структуре сети. Весовые коэффициенты и пороги се­ти Хэмминга определяются из условия задачи, поэтому такая сеть яв­ляется нейронной сетью с фиксированными связями.

Архитектура сети

Сеть Хэмминга является трехслойной сетью, состоящей из различных классов нейронных сетей: сети с пря­мыми связями, сети Хопфилда и слоя выходных нейронов (рис.2.9).

Рис.2.9. Архитектура нейронной сети Хэмминга

Сеть с прямы­ми связями состоит из п входных рас­пределительных и т выходных ней­ронных элементов. Она вычисляет меру подобия между входным и эталонными образами, хранящимися в ней. В качестве меры подобия используется число одинаковых разрядов между входным и эталонным образом. Тогда выходное значение i-гo нейрона второго слоя представляет собой меру подо­бия Р, между входным и i-м эталонным образом:

P_i=n-d_i,

где d, — расстояние Хэмминга между входным и i-м эталонным паттерном.

В процессе функционирования сети можно выделить три фазы. В первой на ее вход подается N-элементный вектор X. После предъявления этого вектора на выходах нейронов первого слоя генерируются сигналы, задающие начальные состояния нейронов второго слоя.

Во второй фазе инициировавшие слой Хопфилда сигналы удаляются, и из сформированного ими начального состояния запускается итерационный процесс внутри этого слоя. Итерационный процесс завершается в момент, когда все нейроны, кроме одного (победителя с выходным сигналом, равным 1), перейдут в нулевое состояние. Нейрон-победитель с ненулевым выходным сигналом становится представителем класса данных, к которому принадлежит входной вектор.

В третьей фазе этот же нейрон посредством весов, связывающих его с нейронами выходного слоя, формирует на выходе сети реакцию в виде вектора у, соответствующий возбуждающему вектору х.

Сеть Хопфилда используется для разрешения возникающих конфликтов, когда входной паттерн является подобным нескольким эталонным образам, хранящимся в сети. При этом на выходе сети ос­тается активным только один нейрон-победитель. Если их несколько, то выбор одного из них происходит случайным образом.

Выходной слой нейронной сети состоит из m нейронов, каждый из которых имеет пороговую функцию активации. Если входной образ не совпадает с эталонным, то на выходе сети Хэмминга будет формироваться такой эталонный паттерн, который имеет минимальное расстояние Хэмминга по от­ношению к выходному образу.

ЛЕКЦИЯ №3

В процессе функционирования нейронная сеть формирует выходной сигнал У в соответствии с входным сигналом X, реали­зуя некоторую функцию g: Y = g(Х). Если архитектура сети задана, то вид функции g определяется значениями синаптических весов и смещений сети. Обозначим через G множество всех возможных функций g, соответствующих заданной архитектуре сети.

Пусть решение некоторой задачи есть функция r. Y = r(Х), заданная парами входных-выходных данных (X¹, У¹), ..., (У^k, У^k), для которых У^k= r(X^k), k= 1...N. Е- функция ошибки (функционал качества), показывающая для каждой из функций g степень близо­сти к r.

Обучить нейронную сеть заданной архитектуры - это значит построить (синтезировать) функцию g € G, подобрав параметры нейронов (синаптические веса и смещения) таким образом, чтобы функционал качества об­ращался в оптимум для всех пар (X^k, У^k).

Функция Е может иметь произвольный вид. Если выбраны множество обучающих примеров и способ вычисления функции ошибки, обучение нейронной сети превращается в задачу много­мерной оптимизации, для решения которой могут быть использо­ваны следующие методы:

• локальной оптимизации с вычислением частных произ­водных первого порядка;

• локальной оптимизации с вычислением частных произ­водных первого и второго порядка;

• стохастической оптимизации;

• глобальной оптимизации.

К первой группе относятся: градиентный метод (наискорей­шего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряжен­ных градиентов; методы, учитывающие направление антиградиен­та на нескольких шагах алгоритма.

Ко второй группе относятся: метод Ньютона, методы опти­мизации с разреженными матрицами Гессе, квазиньютоновские методы, метод Гаусса-Ньютона, метод Левенберга-Маркардта.

Стохастическими методами являются: поиск в случайном направлении, имитация отжига, метод Монте-Карло (численный метод статистических испытаний).

Задачи глобальной оптимизации решаются с помощью пе­ребора значений переменных, от которых зависит целевая функ­ция.

Для сравнения методов обучения нейронных сетей необхо­димо использовать два критерия:

• количество шагов алгоритма для получения решения;

• количество дополнительных переменных для организа­ции вычислительного процесса.

Обучение персептрона

Первое систематическое изучение искусственных нейронных сетей было предпринято Маккалокком и Питтсом в 1943 г. [I]. Позднее в работе [3] они исследовали сетевые парадигмы для распознавания изображений, подвергаемых сдвигам и поворотам. Простая нейронная модель, показанная на рис. 2.1, использовалась в большей части их работы.

Рис. 2.1. Персептронный нейрон

Простая нейронная модель, показанная на рис. 2.1, использовалась в большей части их работы. Элемент Σ умножает каждый вход х на вес w и суммирует взвешенные входы. Если эта сумма больше заданного порогового значения, выход равен единице, в противном случае – нулю. Эти системы (и множество им подобных) получили название персептронов. Они состоят из одного слоя искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов (см. рис. 2.2), хотя в принципе описываются и более сложные системы.

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход.

Алгоритм обучения может быть представлен следующим образом:

1. Подать входной образ и вычислить Y.

2 а. Если выход правильный, то перейти на шаг 1;

б. Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или

в. Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.

3. Перейти на шаг 1.

За конечное число шагов сеть научится разделять входные вектора на два класса при условии, что множество цифр линейно разделимо. Это значит, что для одних образов выход будет больше порога, а для других – меньше. Отметим, что это обучение глобально, т. е. сеть обучается на всем множестве образов. Возникает вопрос о том, как это множество должно предъявляться, чтобы минимизировать время обучения. Должны ли элементы множества предъявляться последовательно друг за другом или их следует выбирать случайно?

Дельта-правило

Важное обобщение алгоритма обучения персептрона, называемое дельта-правилом, переносит этот метод на непрерывные входы и выходы. Шаг 2 алгоритма обучения персептрона может быть сформулирован в обобщенной форме с помощью введения величины δ, которая равна разности между требуемым или целевым выходом T и реальным выходом Y

δ = (T - Y). (2.3)

Случай, когда δ=0, соответствует шагу 2а, когда выход правилен и в сети ничего не изменяется. Шаг 2б соответствует случаю δ > 0, а шаг 2в случаю δ < 0.

В любом из этих случаев персептронный алгоритм обучения сохраняется, если δ умножается на величину каждого входа х_i и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент «скорости обучения» η), который умножается на δх_i, что позволяет управлять средней величиной изменения весов.

В алгебраической форме записи

Δ_i = ηδx_i, (2.4)

w(n+1) = w(n) + Δ_i, (2.5)

где Δ_i – коррекция, связанная с i-м входом х_i; w_i(n+1) – значение веса i после коррекции; w_i{n) -значение веса i до коррекции.

Дельта-правило модифицирует веса в соответствии с требуемым и действительным значениями выхода каждой полярности как для непрерывных, так и для бинарных входов и выходов. Эти свойства открыли множество новых приложений.

Обучение без учителя

Правило обучения Хебба.(+Кохонена)

Согласно этому правилу, обучение происходит в результате усиления силы связи (синаптического веса) между одновременно активными нейронами. Исхо­дя из этого, часто используемые в сети связи усиливаются, что объясня­ет феномен обучения путем повторения и привыкания.

Пусть имеются два нейронных элемента i и j, между которыми существует сила связи, равная w_ij (рис. 3.1):

Рис. 3.1 Взаимосвязь двух нейронов

Тогда правило обучения Хебба можно записать следующим образом:

w_ij (t + 1) = w_ij (t) + x_iy_j

где t - время; х, и у,- - соответственно выходное значение i-го и j-го нейронов.

В начальный момент времени предполагается, что w_ij (t=0)=0, для всех i и j.

Рассмотрим применение пра­вила Хебба для простейшей ней­ронной сети, состоящей из двух входных и одного выходного ней­ронов (см.рис. 3.2). В такой сети по­рог выходного нейронного элемен­та является скрытым в этом эле­менте. При операциях с нейронны­ми сетями порог нейронного элемента можно вынести за его пределы и изобразить как синаптическую связь (рис. 3.2) с весовым коэффициентом, равным значению Т .

Рис. 3.2. Представление порогового значения в виде синаптической связи

Так как входное значение, подаваемое на дополнительный ней­рон, равняется -1, то взвешенная сумма

S=w₁₁x₁+w₂₁x₂-T

Обучение ней­ронной сети происходит путем настройки весовых коэффициентов и порогов нейронных элементов. Поэтому рассмотренное выше преоб­разование позволяет настраивать весовые коэффициенты и пороги се­ти как единое целое.

Правило Хебба для нейронной сети, изображенной на рис. 3.2, можно представить в виде выражений

w₁₁ (t + 1) = w₁₁ (t) + x₁y₁

w₂₁ (t + 1) = w₂₁ (t) + x₂y₁

T(t+1)=T(t)-y₁

Аналогичным образом правило Хебба записывается для нейрон­ной сети большей размерности.

Рассмотрим матричную формулировку правила Хебба. Пусть L -число входных образов, подаваемых на нейронную сеть, n - размер­ность одного образа. Тогда совокупность входных образов можно представить в виде матрицы

где соответствует L -му входному образу.

Весовые коэффициенты нейронной сети, можно также предста­вить в виде матрицы. Тогда матрица взвешенной суммы

S = XW

а матрица выходных значений нейронной сети

Y = F(S)

Правило Хебба в матричной форме можно представить в сле­дующем виде:

W = X^TY.

Правило Хебба может использоваться как при обучении с учите­лем, так и без него. Если в качестве выходных значений у нейронной сети используются эталонные значения, то это правило будет соответ­ствовать обучению с учителем. При использовании в качестве y ре­альных значений, которые получаются при подаче на вход сети вход­ных образов, правило Хебба соответствует обучению без учителя.

В последнем случае весовые коэффициенты нейронной сети в начальный момент времени инициализируются случайным образом. Обучение с использованием правила Хебба заканчивается после пода­чи всех имеющихся входных образов на нейронную сеть. В общем случае правило Хебба не гарантирует сходимости процедуры обучения нейронной сети.

Обучение c учителем

Метод обратного распространения сигнала ошибки

Обозначения

Будем рассматривать трехслойные нейронные сети, аналогичные показанной на рис. 3.3, где O_k, О_j и О_i — выходные величины выходного, скрытого и входного слоев со­ответственно. Вес связи между j-м элементом скрытого слоя и k-м элементом выходного слоя будем обозначать как W_kj.

Рис. 3.3. Многослойная НС

Ана­логично вес связи между i-м элементом входного слоя и j-м эле­ментом скрытого слоя будем обозначать как W_ji. Таким обра­зом, на выходном слое

а на скрытом слое

где

Процедура обучения включает представление набора пар входных и выходных образов. Сначала нейронная сеть на ос­нове входного образа создает собственный выходной образ, а затем сравнивает его с желаемым (целевым) выходным обра­зом. Если различий между фактическим и целевым образом нет, то обучения не происходит. В противном случае веса связей изменяются таким образом, чтобы различие уменьшилось. В качестве меры различия будем использовать функцию квадрата ошибки Е:

где — τ_pk желаемый выход для k-й компоненты р-го выходного образа и O_pk — соответствующий фактический выход. Таким образом, Е_р — мера ошибки вход/выход для р-го образа, Е — общая мера ошибки.

ВЫВОД АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ

Порядок реализации алгоритма обратного распространения

Алгоритм обратного распространения может быть представ­лен в виде следующих шагов.

Шаг 1. Присвоить начальные значения величинам W_ji , W_kj , θ_k, θ_j, η и ά.

Шаг 2. Подать на нейронную сеть входной сигнал. Задать соответствующий ему желаемый выход τ_k, вычислить O_k, О_j и δ_k по формуле:

Шаг 3. Изменить веса связей на величину:

Шаг 4. Вычислить δ_j по формуле:

Шаг 5. Изменить веса связей на величину:

Шаг 6. Положить t->t+l и перейти к шагу 2.

Свойства алгоритма обратного распространения

Алгоритм обратного распространения, полученный на ос­нове градиентного метода наискорейшего спуска, предназна­чен для поиска минимума ошибки, что приводит, однако, к поиску локального минимума или точки перегиба (плато), как показано на рис. 3.4 В идеальном случае должен отыски­ваться глобальный минимум, представляющий собой нижнюю точку на всей области определения. Так как локальный мини­мум окружен более высокими точками, стандартный алгоритм обратного распространения обычно не пропускает локальных минимумов.

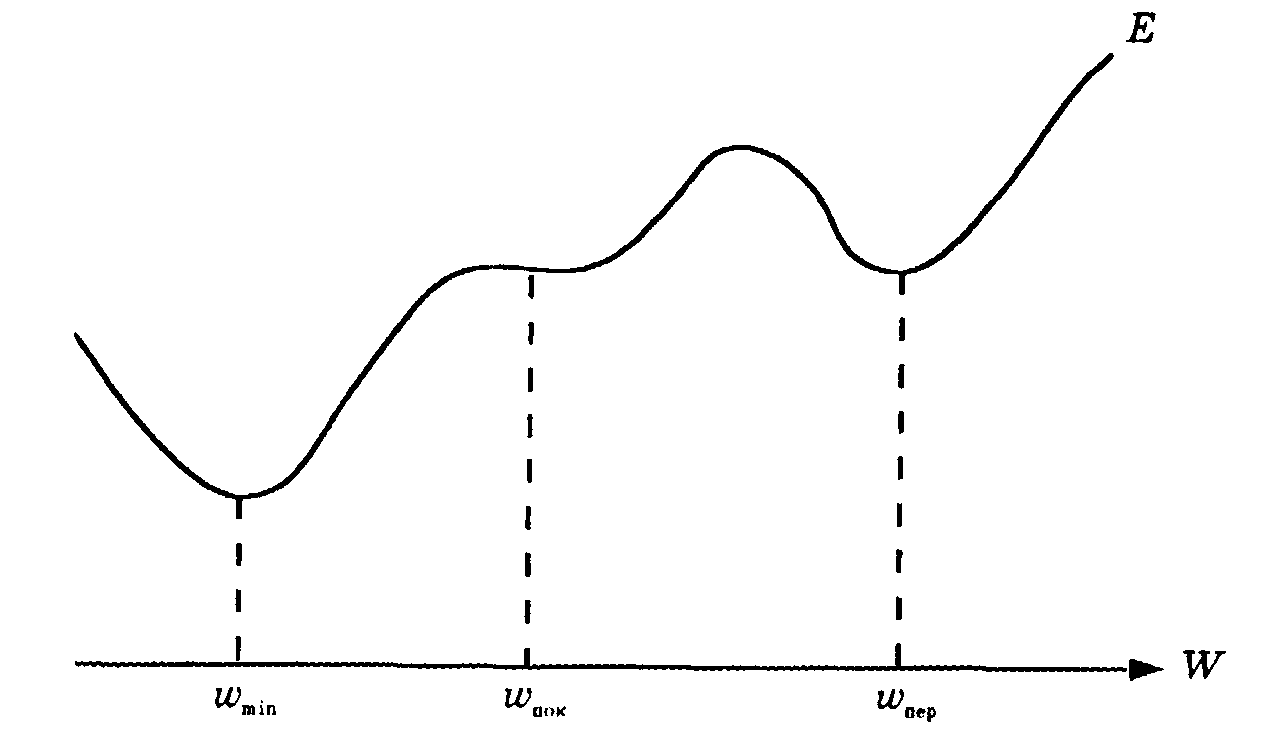
Рис. 3.4 Локальный минимум

Вид локального минимума не всегда представляет суще­ственный интерес. Можно ожидать, что в ходе обучения в со­ответствии с алгоритмом обратного распространения ошибка сети будет сходиться к приемлемому значению, если обучаю­щие образцы четко различимы. Чтобы избежать локальных минимумов, можно изменять параметры обуче­ния, количество скрытых слоев, начальные значения весов связей. Эти методы разрабатываются так, чтобы по­пытаться изменить сценарий перемещения по участку, содер­жащему локальные минимумы и максимумы. Для поиска дос­таточно приемлемых значений параметров алгоритма обрат­ного распространения в последнее время используется генети­ческий алгоритм.

Для вывода алгоритма обратного распространения использована сигмоидная функ­ция. Могут использоваться и другие функции актива­ции. Если, например, использовать функцию вида:

Таким образом, потребовалось только заменить выражения δ_k и δ_j, полученные по формулам на выражения δ_k / T и δ_j / T соответственно. Если выбрать меньшее значе­ние Т, то δ_k и δ_j увеличатся, и в результате скорость изменения весов связей также увеличится. Однако если выбрать большее значение Т, то δ_k и δ_j уменьшатся, и в результате скорость изме­нения весов связей также уменьшится. Таким образом, изме­няя величину Т в процессе обучения, можно управлять скорос­тью сходимости алгоритма обратного распространения.

Скорость обучения η — это константа, представляющая со­бой коэффициент пропорциональности между изменением веса связи и градиентом ошибки Е относительно веса. Чем больше данная константа, тем больше изменения в весах связей. Обыч­но скорость обучения выбирается как можно большей, но та­кой, чтобы не возникало осцилляции. Так как для исключе­ния осцилляции в формулы был введен момент времени, тре­буется выбрать подходящее значение ά. Введение момента вре­мени «отфильтровывает» высокочастотные изменения поверхности ошибки в пространстве весов связей. Это полезно в случаях, когда пространство весов связей содержит длинные овраги с острыми искривлениями. В связи с тем, что такое ис­кривление вызывает резкие расходящиеся колебания в доли­не, необходимо выбирать небольшой размер шага, для чего требуется небольшая скорость обучения. Рекомендуется использовать величи­ну ά, приблизительно равную 0,9.

Лекция №4 Глобальная оптимизация

Алгоритм имитации отжига

Метод имитации отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига (управляемого охлаждения. - Примеч. ред.) при температуре, последовательно понижаемой до нуля. При отвердевании расплавленного материала его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии - глобальному минимуму. В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация тела сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве тела для предотвращения слишком быстрого его остывания. Благодаря допустимости кратковременного повышения энергетического уровня возможен выход из ловушек локальных минимумов, которые возникают при реализации процесса. Только понижение температуры тела до абсолютного нуля делает невозможным какое-либо самостоятельное повышение его энергетического уровня. В этом случае любые внутренние изменения ведут только к уменьшению общей энергии тела.

В реальных процессах кристаллизации твердых тел температура пони­жается ступенчатым образом. На каждом уровне она какое-то время поддерживается постоянной, что необходимо для обеспечения терми­ческого равновесия. На протяжении всего периода, когда температура оста­ется выше абсолютного нуля, она может как понижаться, так и повышаться. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия, удается обходить ловушки локальных минимумов, что при достижении нулевой температуры позволяет получить и минимальный энергетический уровень.

Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953 г. и доработанный многочисленными после­дователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих практически находить глобальный минимум функции нескольких переменных.

Классический алгоритм имитации отжига можно описать следующим образом.

1. Запустить процесс из начальной точки w при заданной начальной температуре Т= Тmах.

2. Пока T > 0, повторить L раз следующие действия:

• выбрать новое решение w' из окрестности w;

• рассчитать изменение целевой функции Δ = E(w') - E(w);

• если Δ <= 0, принять w = w'; в противном случае (при Δ > 0) принять, что w = w' с вероятностью ехр(-Δ /Т) путем генерации случайного числа R из интервала (0,1) с последующим сравнением его со зна­чением ехр(-Δ /Т); если ехр(-Δ /Т) > R, принять новое решение w = w '; в противном случае проигнорировать его.

3. Уменьшить температуру (Т < rТ) с использованием коэффициента уменьшения r, выбираемого из интервала (0,1), и вернуться к п. 2.

4. После снижения температуры до нулевого значения провести обучение сети любым из представленных выше детерминированных методов, вплоть до достижения минимума целевой функции.

В описании алгоритма в качестве названия параметра, влияющего на вероятность увеличения значения целевой функции, используется выбран­ный его автором Н. Метрополисом термин "температура", хотя с формальной точки зрения приведенная модель оптимизации является только математической аналогией процесса отжига. Алгоритм имитации отжига выглядит кон­цептуально несложным и логически обоснованным. В действительности приходится решать много фундаментальных проблем, которые влияют на его практическую применимость. Первой следует назвать проблему длительности имитации. Для повышения вероятности достижения глобального минимума длительность отжига (представляемая количеством циклов L, повторяемых при одном и том же значении температуры) должна быть достаточно большой, а коэффициент уменьшения температуры r - низким. Это увели­чивает продолжительность процесса моделирования, что может дискреди­тировать его с позиций практической целесообразности.

Возникает проблема конкурентоспособности метода по сравнению, например, с методами локальной оптимизации в связи с возможностью многократного возобновления процесса из различных точек в пространстве параметров. При таком подходе грамотная статистическая обработка позволяет с высокой вероятностью и достаточно быстро локализовать зону глобального минимума и достичь его с применением технологии детерминированной оптимизации.

Большое влияние на эффективность метода имитации отжига оказывает выбор таких параметров, как начальная температура T_mах, коэффициент уменьшения температуры г и количество циклов L, выполняемых на каждом температурном уровне.

Максимальная температура подбирается по результатам многочисленных предварительных имитационных экспериментов. На их основе строится распределение вероятности стохастических изменений текущего решения при конкретных значениях температуры (зависимость А = f/(T)). В последующем, задаваясь процентным значением допустимости изменений в качестве порогового уровня, из сформированного распределения можно найти искомую начальную температуру. Главной проблемой остается определение порогового уровня, оптимального для каждой реализации процесса имитации отжига. Для отдельных практических задач этот уровень может иметь различные значения, однако общий диапазон остается неизменным. Как правило, начальная температура подбирается так, чтобы обеспечить реализацию порядка 50% последующих случайных изменений решения. Поэтому знание предварительного распределения вероятностей таких изменений позволяет получить приблизительную оценку начальной температуры.

Методики выбора как максимального количества циклов L для кон­кретных температурных уровней, так и определение значения коэффи­циента уменьшения температуры r не столь однозначны. При подборе этих параметров приходится учитывать динамику изменения величины целевой функции в зависимости от количества выполненных циклов обучения.

Большая часть вычислительных ресурсов расходуется на начальной стадии процесса, когда средняя скорость изменения целевой функции неве­лика и прогресс оптимизации минимален. Это "высокотемпературная" стадия имитационного процесса. Быстрее всего величина целевой функции уменьшается на средней стадии процесса при относительно небольшом количестве приходящихся на нее итераций. Завершающая стадия процесса имеет стабилизационный характер. На ней независимо от количества итераций прогресс оптимизации становится практически незаметным. Такое наблюдение позволяет существенно редуцировать начальную стадию отжига без снижения качества конечного результата. Модификации обычно подвергается количество циклов, выполняемых при высоких температурах, оно сокращается в случае, когда оказался выполненным весь запланированный объем изменений текущего решения. Такой подход позволяет сэкономить до 20% времени.

Исключение последней, плоской части характеристической кривой целевой функции также возможно. В соответствии с обычным критерием остановки алгоритма, если при нескольких последовательных снижениях температуры не регистрируется уменьшение величины целевой функции, то процесс останавливается, а наилучшее достигнутое решение считается глобальным минимумом. Дальнейшее уменьшение критерия остановки не рекомендуется, поскольку оно ведет к снижению вероятности достижения глобального минимума. В то же время заметное влияние на конечную стадию процесса оказывают коэффициент понижения температуры r и количество циклов L. Ее длительность удается сократить более частым изменением температуры при уменьшении количества циклов, но при сохранении неизменным общего объема итераций.

Еще одна проблема связана с определением длительности моделирования процесса отжига, пропорциональной суммарному количеству итераций. Поскольку отводимое для оптимизации время всегда ограничено, все его можно потратить либо на одну реализацию процесса с соответствующим удлинением циклов, либо сократить длительность всех циклов, а за счет этого выполнить несколько реализаций и принять в качестве результата наилучшее решение. В ходе различных компьютерных экспериментов установлено, что при малом лимите времени лучшие результаты дает единичная реализация. Если же моделирование может быть более длительным, статистически лучшие результаты достигаются при многократной реализации процесса имитации отжига, при больших (близких к 1) значениях коэффициента r.

Наибольшее ускорение процесса имитации отжига можно достичь путем замены случайных начальных значений весов w тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных. В такой ситуации в зависимости от количества оптимизируемых весов и степени оптимальности начальных значений удается добиться даже многократного сокращения времени моделирования.

Таким образом, метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с весьма большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами, приведенными в предыдущем подразделе.

Генетические алгоритмы

Идея генетических алгоритмов была предложена Дж. Холландом в 70-х годах XX в., а их интенсивное развитие и практическая реализация для численных оптимизационных расчетов были инициированы Д. Гольдбергом. Эти алгоритмы имитируют процессы наследования свойств живыми организмами и генерируют последовательности новых векторов w, содержащие оптимизированные переменные: w = [w₁, w₂,...,w_n]^T. При этом выполняются операции трех видов: селекция, скрещивание и мутация.

Отдельные компоненты вектора w могут кодироваться в двоичной системе либо натуральными числами. При двоичном кодировании применяется обычный код, или код Грея. После соответствующего масштабирования отдельные биты представляют конкретные значения параметров, подлежащих оптимизации. Каждому вектору w сопоставляется определенное значение целевой функции. Генетические операции (селекция, скрещивание и мутация) выполняются для подбора таких значений переменных w_i вектора w, при которых максимизируется величина функции приспо­собленности (англ.: fitness function). Функция приспособленности F(w) определяется через целевую функцию E(w) путем ее инвертирования (целевая функция минимизируется, а функция приспособленности максимизируется). Например, она может иметь вид: F(w) = -E(w).

На начальной стадии выполнения генетического алгоритма инициали­зируется определенная популяция хромосом (векторов w). Она формируется случайным образом, хотя применяются также и самонаводящиеся спо­собы (если их можно определить заранее). Размер популяции, как правило, пропорционален количеству оптимизируемых параметров. Слишком малая популяция хромосом приводит к замыканию в неглубоких локальных минимумах. Слишком большое их количество чрезмерно удлиняет вычислительную процедуру и также может не привести к точке глобального минимума. При случайном выборе векторов w, составляющих исходную популяцию хромосом, они статистически независимы и представляют собой начальное погружение в пространство параметров. Одна часть этих хро­мосом лучше "приспособлена к существованию" (у них большие значения функции соответствия и меньшие - целевой функции), а другая часть хуже. Упорядочение хромосом в популяции, как правило, производится в направлении от лучших к худшим. Хромосомы отбираются (подвергаются селекции) для формирования очередного поколения по значениям функции соответствия.

Селекция хромосом для создания нового поколения может основываться на различных принципах. Одним из наиболее распространенных считается принцип элитарности, в соответствии с которым наиболее приспособленные хромосомы сохраняются, а наихудшие отбраковываются и заменяются вновь созданным потомством, полученным в результате скрещивания пар родителей. На этапе скрещивания подбираются такие пары хромосом, потомство которых может быть включено в популяцию путем селекции. В случае турнирной системы случайным образом отбирается несколько хромосом, среди которых определяются наиболее приспособленные (с наименьшим значением целевой функции). Из победителей последовательно проведенных турниров формируются пары для скрещивания.

При взвешенно-случайной системе в процессе отбора учитывается информация о текущем значении функции приспособленности. Отбор может происходить по принципу "рулетки", при этом площадь сегмента колеса рулетки, сопоставленного конкретной хромосоме, пропорциональна величине ее относительной функции приспособленности. Ситуация, типичная для такого отбора, иллюстрируется на рис. 3.5. Полная площадь круга соответствует сумме значений функций приспособленности всех хромосом данной популяции. Каждый выделенный сегмент отвечает конкретной хромосоме. Наиболее приспособленным особям отводятся большие сегменты колеса рулетки, увеличивающие их шансы попадания в переходную популяцию.

Рис. 3.5. Схема "рулетки", используемая при выборе родителей для будущего поколения. Площадь отдельных сегментов пропорциональна значениям соответствующих функций

приспособленности

Процесс скрещивания основан на рассечении пары хромосом на две части (рис. 3.10) с последующим обменом этих частей в хромосомах родителей. Место рассечения также выбирается случайным образом.

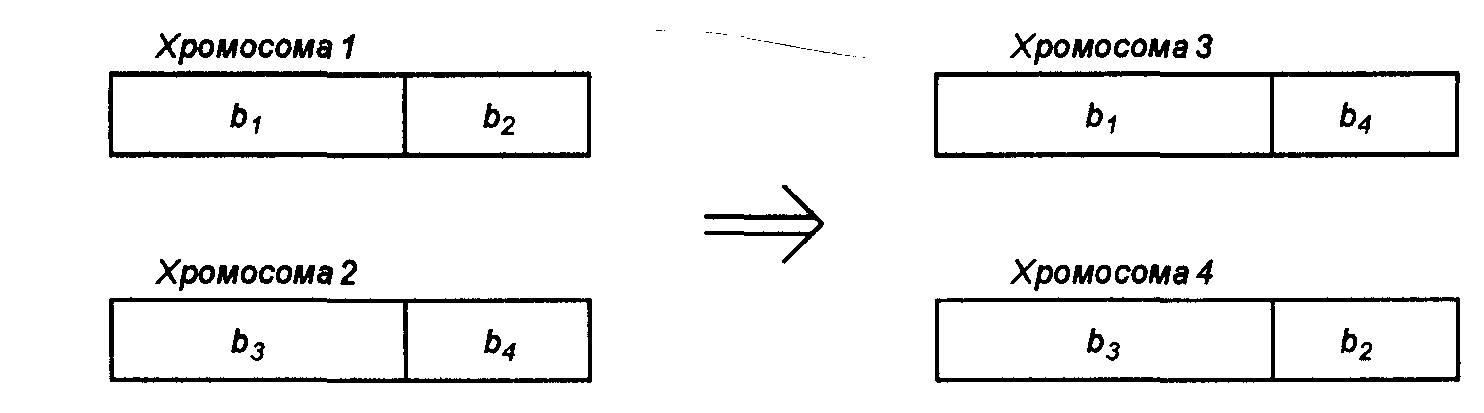
Рис. 3.6. Иллюстрация операции скрещивания, применяемой в генетическом алгоритме

В ситуации, показанной на рис. 3.6, после скрещивания хромосомы 1 с хромосомой 2 образовалась пара новых хромосом: хромосома 3 и хромосома 4. Количество новых потомков равно количеству отбракованных в результате селекции. После их добавления к оставшимся хромосомам размер популяции остается неизменным. Как правило, признается допустимым перенос в очередное поколение некоторых случайно выбранных хромосом вообще без скрещивания. Это соответствует ситуации, когда скрещивание достигает успеха с определенной вероятностью, обычно на уровне 0,6-1.

Мутация – это генетическая операция состоящая в замене значений отдельных битов (при двоичном кодировании) на противоположные. При кодировании натуральными десятичными цифрами мутация заключается в замене значения какого-либо элемента вектора другим, случайно выбранным допустимым значением. Мутация обеспечивает защиту как от слишком раннего завершения алгоритма (в случае выравнивания значений всех хромосом и целевой функции), так и от представления в какой-либо конкретной позиции всех хромосом одного и того же значения. Однако необходимо иметь в виду, что случайные мутации приводят к повреждению уже частично приспособленных векторов. Обычно мутации подвергается не более 1-5% бит всей популяции хромосом. Как и при выполнении большинства генетических операций, элемент, подвергаемый мутации, отбирается случайным образом.

Исследованиями доказано, что каждое последующее поколение, сформированное после выполнения селекции, скрещивания и мутации, имеет статистически лучшие средние показатели приспособленности (меньшие значения целевой функции).

В качестве окончательного решения принимается наиболее приспособленная хромосома, имеющая минимальное значение целевой функции. Генетический процесс завершается либо в момент генерации удовлетворяющего нас решения, либо при выполнении максимально допустимого количества итераций. При реализации генетического процесса отслеживается, как правило, не только минимальное значение целевой функции, но и среднее значение по всей популяции хромосом, а также их вариации. Решение об остановке алгоритма может приниматься и в случае отсутствия прогресса минимизации, опреде­ляемого по изменениям названных характеристик.

Хорошие результаты обучения приносит объединение алгоритмов глобальной оптимизации с детерминированными методами. На первом этапе обучения сети применяется выбранный алгоритм глобальной оптимизации, а после дости­жения целевой функцией определенного уровня включается детермини­рованная оптимизация с использованием какого-либо локального алгоритма (наискорейшего спуска, переменной метрики, Левенберга-Марквардта или сопряженных градиентов).