Методичка Зайцева

51

И889

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ

Методические указания и задания к практическим занятиям

Новосибирск 2007

3

УДК 681.306 И889

Исследование операций и методы оптимизации: Метод. указ. и задания к практическим занятиям / Сост. Т.С. Зайцева, И.А. Новицкая, Э.А. Усова, В.И. Хабаров. – Новосибирск: Изд-во СГУПСа, 2007. – 54 с.

Даны основные виды задач различных типов и методические указания к их решению, а также ключевые вопросы для самоконтроля, помогающие самостоятельно анализировать пошагово полученные знания, осваивать основные положения дисциплины «Исследование операций и методы оптимизации», приобретать навыки оформления решений предложенных задач.

Методические указания предназначены для изучения студентами различных специальностей факультетов БИ, МЭ (дневная форма), заочного факультета курсов «Исследование операций», «Математическое программирование», «Исследование операций и методы оптимизации».

Рассмотрены и утверждены к печати на заседании кафедры «Системный анализ и управление проектами».

Ответственный редактор д-р техн. наук, проф. кафедры «Информационные технологии транспорта» В.И. Хабаров

Р е ц е н з е н т ы:

канд. экон. наук, доц. кафедры «Общая информатика» Г.А. Черемных канд. техн. наук, вед. науч. сотр. НИЛ ИТТ А.А. Уланов

©Зайцева Т.С., Новицкая И.А., Усова Э.А., Хабаров В.И., сост., 2007

©Сибирский государственный университет путей сообщения, 2007

4

ВВЕДЕНИЕ

В данных методических указаниях рассмотрены различные классы задач математического программирования и методы их решения:

−первая группа задач — транспортные задачи, задача о назначении, задача выбора;

−ко второй группе задач относятся задачи линейного программирования, решаемые различными методами (прямой сим- плекс-метод, двойственный симплекс-метод);

−задачи нелинейного программирования входят в следующую, третью группу и решаются методом наискорейшего спуска, методом Ньютона, для оценки полученного решения используются методы «золотого сечения», Фибоначчи, квадратичной аппроксимации; задачи выпуклого программирования, решаемые с помощью метода возможных направлений или методом Нелдора – Мида, также входят в данную группу;

−задачи динамического программирования и матричные игры, решаемые симплекс-методом, составляют свой, четвертый класс.

Предложенные варианты содержат задачи небольшой размерности. Это позволяет рассмотреть широкий круг методов решения в ограниченное учебным планом время и провести их геометрическую интерпретацию. Оптимизационные задачи содержат все характерные черты рассматриваемого класса задач.

При выполнении задания студентам рекомендуется как можно больше делать рисунков, проясняющих геометрическую сущность задачи. Наглядность обеспечит более глубокое понимание идеи метода, а также проверку достоверности результата.

Сначала следует детально проработать алгоритм и только после этого приступать к вычислениям. Выполнение алгоритма можно производить с помощью блок-схем либо с помощью языков программирования высокого уровня. Это позволит организовать мышление и использовать для вычислений имеющиеся технические средства.

5

ЗАДАНИЕ № 1

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ТРАНСПОРТНОГО ТИПА

1.1.Задание для предложенного варианта

1.1.1.Привести математическую постановку транспортной задачи (ТЗ).

1.1.2.Найти опорное решение ТЗ методом северо-западного угла и методом минимального элемента. Сравнить по значению целевой функции качество полученных опорных планов.

1.1.3.Получить оптимальный план перевозок методом потенциалов. Сравнить значение целевой функции на каждом шаге метода со значением для опорного плана.

1.1.4.Решить задачу о назначении венгерским методом.

1.2. Методические указания к выполнению задания № 1

Метод потенциалов для решения ТЗ подробно освещен в [1–3]. Необходимо обратить внимание на экономический смысл условий оптимальности решения ТЗ, выражаемых через потенциалы. На каждом шаге реализации метода необходимо эти условия проверять. По возможности следует составить для каждого шага граф перевозок, в котором группа вершин с исходными дугами соответствует пунктам потребления. Дуги соотносятся с ненулевыми перевозками. Каждой вершине соответствует потенциал, а каждой дуге — стоимость перевозки. Данный граф удобно использовать для составления потенциальных уровней.

Рассмотреть ситуацию, когда ТЗ будет вырожденной.

Решая задачу о назначении (задача выбора), необходимо дать ее содержательную, а также математическую постановку. Показать, что эта задача является частным случаем транспортной задачи. Исходными данными для задачи о назначении служит матрица, использованная в ТЗ.

Венгерский метод достаточно полно описан в [1].

1.3.Вопросы для самоконтроля

1.3.1.Сформулируйте условия разрешимости транспортной за-

дачи.

1.3.2.Что называется опорным планом ТЗ?

6

1.3.3.Сформулируйте принцип оптимальности плана ТЗ и объясните экономический смысл понятия потенциала.

1.3.4.Какой план является вырожденным? Как решить ТЗ в условиях вырожденности?

1.3.5.В чем состоит особенность венгерского метода по сравнению с методом потенциалов?

1.3.6.Покажите, что задача о назначении является частным случаем ТЗ.

1.4. Варианты задания

Для каждого варианта исходные данные представлены в табл. 1.1, в которой для ТЗ объем производства отражен в крайнем правом столбце, объем потребления — в нижней строке. Остальные элементы таблицы составляют матрицу стоимостей перевозок.

															Таблица 1.1
	Вариант № 1						Вариант № 2						Вариант № 3
12	11	25	17	21	17	2	24	4	2	3	28	15	6	25	11	12	9
22	18	14	8	1	14	20	10	15	27	7	13	13	14	20	27	30	18
9	13	2	28	15	21	15	15	12	25	19	15	16	7	19	10	21	23
26	21	3	4	27	43	2	6	3	5	5	30	1	29	23	25	18	26
19	22	23	17	14		27	16	25	11	7		11	22	31	6	6
	Вариант № 4						Вариант № 5						Вариант № 6
22	24	25	23	29	24	6	11	20	17	8	12	7	10	16	27	19	17
1	21	10	7	19	14	1	25	3	18	17	17	30	18	8	29	15	19
2	26	18	30	27	19	9	39	16	30	31	18	3	18	28	19	13	11
22	10	29	26	23	17	23	15	4	3	28	13	9	12	2	25	21	13
22	9	12	13	18		10	8	12	14	16		5	15	11	9	20
	Вариант № 7						Вариант № 8						Вариант № 9
4	21	12	8	1	21	5	3	24	10	25	24	21	19	11	12	12	24
20	8	25	15	23	21	30	2	22	16	7	15	26	29	14	1	26	12
17	1	11	5	3	23	30	24	27	29	10	16	39	1	22	8	25	18
23	10	24	6	5	23	15	17	21	2	3	24	53	23	40	26	28	16
22	22	22	11	11		12	13	14	31	9		11	13	26	10	10
	Вариант № 10						Вариант № 11						Вариант № 12
25	28	20	15	7	16	16	30	17	10	16	4	15	1	22	19	1	20
27	5	11	23	10	12	30	27	26	9	23	6	21	18	11	4	3	20
1	25	14	16	16	14	13	4	22	3	1	10	26	29	23	26	24	20
8	6	4	16	18	18	3	1	5	4	24	10	21	10	3	19	27	20
7	8	4	11	30		7	7	7	7	2		19	19	19	19	4

7

													Окончание табл. 1.1
	Вариант № 13						Вариант № 14						Вариант № 15
17	20	29	26	25	15	14	25	18	19	23	23	8	1	19	1	15		18
3	4	5	15	24	15	2	17	16	24	2	25	8	27	30	7	7		23
19	2	22	4	13	15	29	3	7	15	22	25	10	20	19	26	20		17
20	27	1	17	19	15	5	20	17	23	10	17	18	28	25	7	22		22
11	11	11	11	16		33	11	11	11	34		21	21	9	9	20
	Вариант № 16						Вариант № 17						Вариант № 18
30	20	27	15	26	33	11	10	15	8	7	16	20	26	24	26	29		13
25	6	28	20	5	33	12	14	29	20	20	15	15	20	29	26	23		17
19	24	11	29	23	33	18	7	5	25	28	24	4	10	27	30	7		17
1	4	6	6	8	11	24	4	30	24	26	15	9	16	29	30	3		13
22	22	22	22	22		15	15	15	15	10		12	12	12	12	12
	Вариант № 19						Вариант № 20						Вариант № 21
21	22	2	13	7	18	10	17	9	20	30	15	30	24	11	12	25	21
27	10	4	24	9	12	13	4	24	26	26	15	26	4	29	20	24		19
3	16	25	5	4	17	22	24	30	27	29	19	27	14	14	10	18		15
28	11	17	10	29	13	25	12	11	24	23	11	6	14	28	8	2		25
8	8	8	8	28		9	24	9	9	9		15	15	15	15	20
	Вариант № 22						Вариант № 23						Вариант № 24
5	15	3	6	10	9	9	17	29	28	8	22	30	2	5	6	15		16
23	8	13	27	12	11	13	21	27	16	29	13	5	29	9	5		7	15
30	1	5	24	25	14	20	30	24	7	26	17	16	24	14	6	26		14
8	26	7	28	9	16	11	19	30	6	2	18	13	28	4	25		8	15
8	9	13	8	12		7	7	7	7	42		6	6	13	20	15

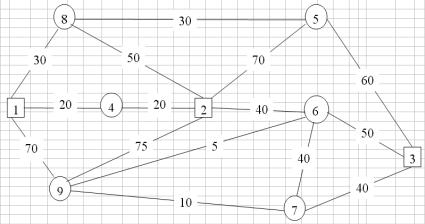
1.5. Постановка транспортной задачи на сети

Сформулировать математическую постановку транспортной задачи применительно к условиям сети ж.-д. траспорта и решить ее, используя исходные данные табл. 1.2 (количество поставляемого и потребляемого груза, усл. ед.). На рисунке показана схема движения груза от поставщиков — к потребителям — .

Схема движения поставляемого и потребляемого груза

8

Таблица 1.2

Варианты
№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
	Поставщики
1	200	100	250	75	150	300	325	200	245	155	325	250	125	250	455	320	255	325	400	635
2	300	300	250	125	200	150	255	415	75	125	250	350	250	325	355	190	390	435	385	215

3100 250 250 200 125 150 125 185 125 300 175 150 350 145 120 385 420 370 375 350 Потребители

4	150	100	50	125	55	30	40	75	80	125	100	75	125	100	350	130	215	270	125	245
5	50	150	100	75	125	125	150	185	45	35	95	65	325	75	125	265	175	255	250	325
6	150	50	75	25	45	50	160	65	65	95	75	110	45	65	45	195	35	160	315	355
7	100	100	125	50	75	145	125	155	150	85	180	300	120	215	140	65	190	245	125	30
8	100	75	200	75	85	150	80	250	65	145	185	140	60	155	155	145	145	45	245	125
9	50	175	200	50	90	100	150	70	40	95	115	60	50	110	115	95	305	155	100	120
Варианты
№	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
	Поставщики
1	325	250	150	300	200	300	455	345	400	345	365	350	250	400	500	425	250	285	300	500
2	245	295	275	345	345	200	315	325	200	365	315	350	230	300	450	125	150	290	200	500
3	365	245	315	255	185	325	125	285	300	385	385	350	280	100	350	325	350	145	400	300
	Потребители
4	245	120	45	155	95	145	175	175	125	150	170	145	85	125	200	200	145	100	85	200
5	50	150	125	200	75	165	180	190	150	140	195	135	65	120	200	140	35	120	55	210
6	150	70	170	170	145	85	130	95	185	130	185	165	185	165	250	140	100	135	45	250
7	100	200	100	90	145	125	140	175	145	180	165	155	155	95	200	120	85	100	225	190
8	110	75	185	135	165	115	95	265	180	190	135	215	125	120	200	125	175	120	235	255
9	280	175	115	150	105	190	175	55	115	305	215	235	145	175	250	150	210	145	255	195
Варианты
№	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
	Поставщики
1	200	250	400	300	550	400	500	400	200	300	250	285	250	400	400	300	500	300	450	350
2	200	350	300	150	250	200	400	300	250	400	350	365	250	300	500	500	500	350	250	380

3200 250 500 250 350 450 500 350 350 500 450 450 350 200 300 400 200 300 250 345 Потребители

4	95	145	210	140	185	150	200	250	150	250	150	175	100	145	200	210	180	100	190	85
5	85	245	220	150	175	125	250	200	120	125	145	190	200	165	125	230	170	100	180	95
6	75	125	230	90	100	150	200	150	130	185	215	185	95	155	180	220	160	100	155	150
7	125	95	250	60	255	250	150	150	150	195	265	250	145	140	150	150	155	150	225	245
8	135	130	145	120	280	200	300	150	125	225	185	175	160	130	250	140	260	250	110	270

985 110 145 140 155 175 300 150 125 220 90 125 150 165 295 250 275 250 90 230

1.6. Задача для решения венгерским методом

Привести математическую постановку Т3 и решить ее венгерским методом. Исходные данные для 36 вариантов представлены в табл. 1.3.

9

Таблица 1.3

№		Условие				№		Условие				№		Условие				№		Условие
вар.						вар.						вар.						вар.
	11		4		5		14		6		5		8		9		11		8		9		2
1	2		16		7	10	5		4		4	19	7		4		8	28	6		9		12
	9		11		6		10		11		12		4		10		4		12		13		3
	7		11		2		10		11		7		10		10		4		7		10		14
2	4		15		14	11	3		3		2	20	14		1		15	29	1		13		7
	4		15		12		13		4		9		2		10		7		6		13		5
	6		3		14		9		13		14		1		6		4		7		10		10
3	14		3		12	12	14		10		5	21	12		2		4	30	8		4		6
	7		12		12		2		10		13		9		4		7		8		12		4
	15		6		8		5		11		4		4		12		6		2		8		3
4	13		10		13	13	16		11		10	22	15		15		2	31	3		15		4
	13		14		11		3		11		5		4		15		2		6		12		3
	10		15		12		11		13		3		9		14		3		14		12		13
5	4		7		8	14	12		10		8	23	14		1		5	32	14		6		7
	3		7		7		12		10		12		5		8		3		4		2		13
	14		12		9		3		15		2		8		1		14		5		5		6
6	6		4		15	15	15		14		6	24	6		5		9	33	7		7		9
	8		13		6		1		10		16		3		15		13		11		6		8
	4		13		3		3		6		9		15		4		5		9		10		2
7	15		16		16	16	11		5		6	25	7		6		14	34	14		9		4
	14		8		11		16		6		3		12		1		10		10		10		6
	2		1		9		2		4		11		13		10		10		5		4		5
8	5		10		14	17	6		12		10	26	16		8		4	35	4		4		10
	13		4		9		4		10		15		16		12		14		2		5		16
	9		13		5		6		15		3		8		4		15		12		11		9
9	7		11		3	18	16		13		2	27	7		9		5	36	13		15		6
	11		16		11		10		11		2		6		7		7		10		2		2

ЗАДАНИЕ № 2

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО

ИЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

2.1.Задание для предложенного варианта

2.1.1.Привести математическую постановку задачи линейного программирования (ЛП).

2.1.2.Дать графическую интерпретацию задачи ЛП и решить ее графическим способом.

2.1.3.Записать задачу ЛП в двойственной формулировке.

2.1.4.Привести графическую интерпретацию двойственной задачи ЛП. Найти графический способ решения двойственной задачи ЛП.

10

2.1.5.Решить задачу линейного программирования с помощью прямого и двойственного симплекс-методов. Сравнить полученные решения с графическими решениями (пп. 2.1.2, 2.1.3).

2.1.6.Привести математическую постановку задачи линейного целочисленного программирования (ЛЦП).

2.1.7.Дать графическую интерпретацию задачи ЛЦП. Выделить множество допустимых точек. Решить графическим способом задачи ЛЦП.

2.1.8.Найти решение задачи ЛЦП с помощью алгоритма Гомори. Сравнить полученное решение с графическим решением.

2.1.9.Найти решение задачи ЛЦП с помощью алгоритма ветвей

играниц (алгоритм Ленг и Дойг).

2.2. Методические указания к выполнению задания № 2

Существует множество вариантов математической записи задачи ЛП. Будем придерживаться следующей формы записи:

			n
			∑c j x j → max;		(2.1)
			j=1	x
		n
	∑ aij x j ≤ bi , (i = 1,2,...,				m );
j =1					(2.2)
			≥ 0, ( j = 1,2,..., n).
x		j

Поскольку в публикациях не существует единообразия, полезно уметь переходить от одной формы записи задачи ЛП к другой. Представленная выше форма записи соответствует стандартной форме, данной в основном учебном пособии [1].

Рассмотрим варианты прямого и двойственного симплексметодов, реализация которых основана на данных симплекстаблицы 2.1.

			Таблица 2.1
Элементы симплекс-таблицы	x1...xj...xn	1	=
y1	a1...aij...am	− b1	− u1
yi	ai1...aij...ain	− bi	− ui
ym	am1...amj...amn	− bm	− um
–1	c1...cj...cn	0	ω
=	υ1...υ j...υn	− ω′

11

x j = 0, j =1,...,n,

В приведенной таблице одновременно представлена прямая и двойственная задачи ЛП. Переменные y1, y2,..., ym соответствуют переменным двойственной задачи. Переменные u1,u2,...,um и υ1,υ2,...,υn приводят ограничения-неравенства соответственно в прямой и двойственной задачах к ограничениям-равенствам. Переменные, находящиеся в верхней строке, называются базисными, а переменные, находящиеся в крайнем правом столбце, – небазисными или свободными. Нетрудно убедиться в том, что если xj и ui

поменять местами, то элементы симплекс-таблицы (2.1) изменяются согласно схеме

			1
p q
			p
		→
				r
r	s		−
				p

q
p
				,	(2.3)
s −		rq
		p

где q — любой элемент i-той строки, r — любой элемент j-го столбца, а p = aij . Элемент р называют ведущим. Преобразование

симплекс-таблицы называют симплекс-преобразованием относительно ведущего элемента р. Симплекс-преобразование играет основную роль в симплекс-методе решения задачи ЛП. Геометрически симплекс-преобразование соответствует переходу от одного базиса n-мерного линейного пространства к другому. Пусть задан некоторый базис, определяемый координатами x1,x2,...,xn. Если по-

ложить то полученная точка будет соответствовать началу координат. Пусть при этом все элементы − bi ,i = 1,...,m отрицательны, тогда согласно (2.1) – (2.3) эта точка будет допустимой, т.е. удовлетворяющей системе неравенств в (2.2). Такая точка также называется базисной.

Геометрическая идея симплекс-метода сводится к последовательному переходу от одной базисной точки к другой с условием, что при таком переходе целевая функция должна строго возрастать. Поскольку количество базисных точек конечно, то число шагов в симплекс-методе также конечно.

Можно выделить два основных этапа решения задачи ЛП — это получение:

– базисного решения;

12