Несобственные интегралы I и II рода

Понятие определенного интеграла было введено для функций, заданных на интервале [a; b]. Однако существуют понятия интеграла на случай функций, определенных на неограниченных интервалах.

Пусть функция определена на бесконечном интервале [a; ) и интегрируема на любом интервале [a; b], где b < .

Несобственным интегралом I рода функции f(x) на интервале [a; ) называется предел

= (6)

Если предел в левой части равенства (6) является конечным числом, то интеграл называетсясходящимся, если этого предела не существует или он равен , то говорят, что интеграл расходится.

Пример 6. Вычислить несобственный интеграл или установить его расходимость.

Решение

Имеем

||=

Тест 6. Вычислить несобственный интеграл или установить его расходимость:

1) расходится;

2)

3) 1;

4)

5) 2.

При введении понятия определенного интеграла предполагалось, что подынтегральная функция на [a; b] является ограниченной. Тем не менее существует обобщение понятия определенного интеграла и на случаи, когда нарушается требование ограниченности подынтегральной функции на [a; b].

Предположим, что f(x) является ограниченной и интегрируемой на любом отрезке [a + ; b], 0 <  < b – a, но неограниченной в любой окрестности точки а. В таком случае точка а называется особой точкой.

Несобственным интегралом II рода функции f(x) на отрезке [a; b] называется предел

=(7)

Если предел в левой части равенства (7) существует и является конечным числом, то интеграл называетсясходящимся. В противном случае он называется расходящимся.

Пример 7. Вычислить несобственный интеграл или установить его расходимость.

Решение

Имеем

|=

Делаем вывод, что данный несобственный интеграл расходится.

Тест 7. Вычислить несобственный интеграл или установить его расходимость:

1) расходится;

2)

3) 1;

4)

5) 2.

Приближенные методы вычисления определенных интегралов

Существует много формул приближенного вычисления определенных интегралов. Приведем наиболее простую из них – формулу трапеций.

Пусть в интеграле функцияf(x) непрерывна на отрезке [a; b]. Разобьем отрезок [a; b] на n равных частей точками =– значение функции=в точкеТогда имеет место так называемая формула трапеций

(8)

Пример 8. Вычислить приближенно определенный интеграл применив формулу трапеций, взявn = 3.

Решение

Находим шаг h: Получаем:x₀ = 1, x₁ = 2, х₂ = 3, х₄ = 4. Тогда соответствующими значениями функции y₀ = 1, Подставляя эти значения в формулу (8), получим

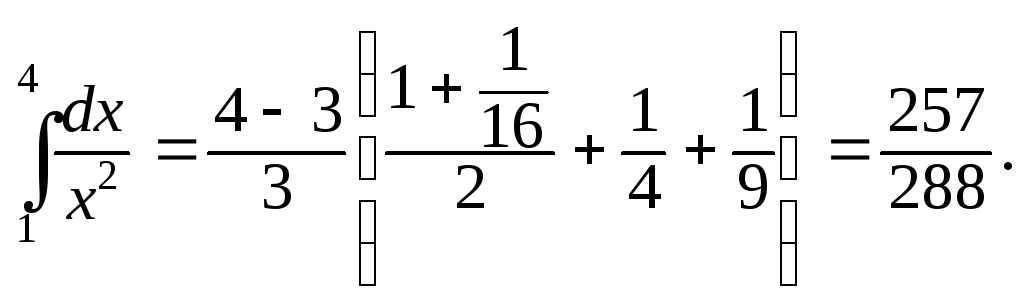
Тест 8. Вычислить приближенно определенный интеграл применив формулу трапеций, взяв n = 4:

1)

2) 2;

3)

4)

5)

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7	8
Правильный ответ	2	1	5	3	2	4	1	5

2.10. Кратные интегралы

Множество точек называется связным, если любые две из них можно соединить линией, все точки которой принадлежат данному множеству.

Под геометрической фигурой Ф будем понимать одно из следующих связных (включая границу) множеств точек:

1) линия L в R² или R³, в частности отрезок [a; b] координатной оси;

2) плоская область D в R² (рисунок 52);

3) поверхность Q в R³ (рисунок 53);

4) пространственная область V в R³, ограниченная замкнутой поверхностью, − тело в пространстве (рисунок 53).

Определение. Диаметром d фигуры Ф называется максимальное расстояние между двумя ее точками.

Пример 1. Диаметр параллелограмма − длина большей диагонали.

В дальнейшем будем рассматривать фигуры конечного диаметра (ограниченные).

Определение. Под мерой фигуры Ф будем понимать: для отрезка [a; b] − его длину |[a; b]|, для линии L − ее длину l, для плоской области D и поверхности Q − их площади s и q соответственно, для пространственной области V − объем v соответствующего тела.

Рассмотрим фигуру Ф, мера которой μ, и определенную на ней непрерывную скалярную функцию f(P), P  Ф. Осуществим построение, геометрическая интерпретация которого применительна к плоской области D. Выбранная в качестве конкретного примера фигура Ф дана на рисунках 52 и 53.

Для этого выполним следующие действия:

1. Разобьем Ф произвольным образом на n элементарных фигур ΔФ_i с мерами Δμ_i, i = 1, 2, , n.

2. На каждой элементарной фигуре выберем произвольную точку P_i ΔФ_i и вычислим значения f(P_i) функции в этих точках.

3. Найдем произведения f(P_i )Δμ_i, i = 1, 2, , n.

4. Составим сумму

S_n = (1)

которую будем называть n-й интегральной суммой для функции f(P) по фигуре Ф.

5. Перейдем к пределу в сумме (1) при условии, что наибольший из диаметров λ элементарных фигур ΔФ_i стремится к 0

S_n =

Очевидно, что для данной фигуры Ф и выбранного n можно составить сколько угодно интегральных сумм, зависящих от разбиения фигуры Ф и выбора точек P_i ΔФ_i.

У

Z

D

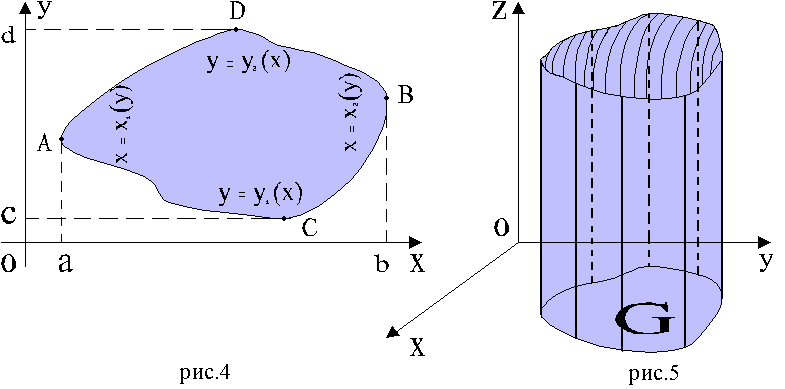
Рисунок 52 Рисунок 53

Определение. Предел n-й интегральной суммы (1) для данной функции f(P) и фигуры Ф при условии, что каждая из элементарных фигур стягивается в точку (λ → 0), если он существует, конечен и не зависит от способа построения интегральной суммы, называется интегралом по фигуре Ф от скалярной функции f(P) и обозначается

= (2)

Теорема. Если на связной, ограниченной и содержащей граничные точки фигуре Ф скалярная функция f(P) непрерывна, то интеграл по фигуре Ф от этой функции существует.