Частные случаи интегралов по фигуре (кратных интегралов) Определенный интеграл

Пусть Ф – отрезок [a; b] координатной оси Ох. Мерой μ отрезка [a; b] является его длина, μ = |[a; b]| = b – a. Обозначим также Δμ_i = Δx_i и λ = max{Δx_i}, i = 1, 2, …, n. Тогда интегральная сумма (1) для функции f(P) = f(x) примет вид

S_n ==

и ее предел, если он существует, называется определенным интегралом (однократным интегралом) и обозначается

= =

где Ф = [a; b] – отрезок интегрирования;

x – переменная интегрирования;

a и b – соответственно нижний и верхний пределы интегрирования.

Двойной интеграл

Пусть фигура Ф – плоская область D, которой принадлежит ее граница (кривая L). Мерой μ такой фигуры является его площадь s, т. е. μ = s. Обозначим также Δμ_i = Δs_i и λ = max{Δs_i}, i = 1, 2, , n. Тогда интегральная сумма (1) для функции z = f(P) = f(x; y) примет вид

S_n ==

и ее предел, если он существует, называется двойным интегралом от функции z = f(x; y) по области D и обозначается

== (3)

где D – область интегрирования;

x, y – переменные интегрирования;

dxdy – дифференциал площади плоской области D.

Тройной интеграл

Пусть фигура Ф – область V  R³, ограниченная замкнутой поверхностью. Мерой μ такой фигуры является его объем v, т. е. μ = v. Обозначим также Δμ_i = Δv_i и λ = max{Δv_i}, i = 1, 2, …, n. Тогда интегральная сумма (1) для функции f(P) = f(x; y; z), P  V, примет вид

S_n ==

и ее предел, если он существует, называется тройным интегралом от функции f(x; y; z) по пространственной области D и обозначается

==

где V – область интегрирования;

x, y, z – переменные интегрирования;

dxdydz – дифференциал объема пространственной области V.

Свойства интегралов по фигуре (кратных интегралов). Свойства интегралов по фигуре аналогичны свойствам однократных определенных интегралов как частным случаям интеграла по фигуре.

Геометрический смысл двойного интеграла. Пусть функция z = f(P) = f(x; y) принимает в области D только положительные значения. Тогда двойной интеграл численно равен объему V вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности z = f(x; y) (рисунки 53 и 54).

Рисунок 54

Вычисление двойного интеграла

1. Пусть функция f(x; y) непрерывна в области D. Если D – прямоугольник, то при вычислении двойного интеграла имеет место формула

(4)

которая показывает, что порядок интегрирования можно менять.

Интеграл (4) представляет собой объем тела, ограниченного снизу прямоугольником P, сбоку – боковыми гранями прямой призмы, построенной на этом прямоугольнике, а сверху – той частью поверхности, которая вырезана этой призмой (рисунок 55).

Рисунок 55

2. Если функция f(x; y) непрерывна на множестве D = {(x; y): a ≤ x ≤ b, y₁(x) ≤ y ≤ y₂(x)}, где y₁(x) и y₂(x) непрерывны на отрезке [a; b] и y₁(x) ≤ ≤ y₂(x) на [a; b] (область D правильная в направлении оси OY, т. е. любая прямая, параллельная оси OY, пересекает область D не более чем в двух точках) (рисунок 56), то верно равенство

(5)

Правая часть в формуле (4) называется повторным интегралом, a и b − его внешними пределами (они всегда постоянны), y₁(x) и y₂(x) − внутренними пределами интегрирования (они могут быть переменными и постоянными). Вначале вычисляется внутренний интеграл, при этом вторая переменная (в данном случае x), соответствующая внешнему интегралу, считается постоянной, а затем – внешний интеграл с последующим применением формулы Ньютона-Лейбница.

3. Если функция f(x; y) непрерывна в области D (рисунок 57), D = {(x; y): c ≤ y ≤ d, x₁(y) ≤ x ≤ x₂(y), где функции x₁(y) и x₂(y) непрерывны на сегменте [c; d] и x₁(y) ≤ x₂(y) на [c; d] (область D правильная в направлении оси OX, т. е. любая прямая, параллельная оси OX, пересекает область D не более чем в двух точках), то верно равенство

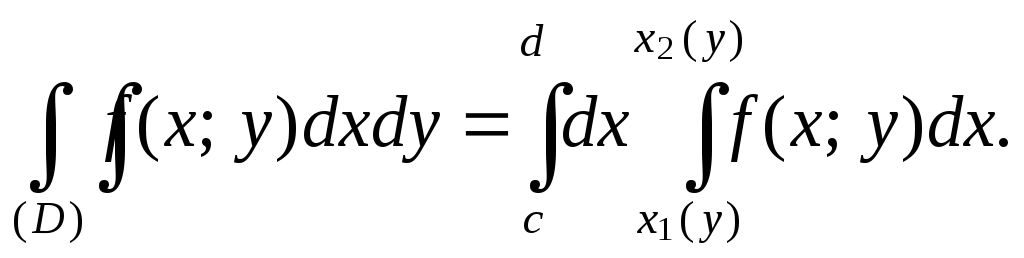(6)

Рисунок 56 Рисунок 57

4. Если область D такова (рисунок 52), что к ней применима и формула (5), и формула (6), то

Это равенство используется для перемены порядка интегрирования в повторном интеграле.

Области более сложного вида следует разбить на части, к которым применима формула (5) или (6).