IV. Проверочная работа.

– Решите задачи:

В а р и а н т 1

1. Два последовательных чётных числа таковы, что квадрат большего из них в 9 раз больше меньшего числа. Найдите эти числа.

2. Одну сторону квадрата уменьшили на 2 см, а другую – на 1 см и получили прямоугольник с площадью 6 см². Найдите длину стороны квадрата. Изобразите квадрат и прямоугольник.

В а р и а н т 2

1. Два последовательных нечётных числа таковы, что квадрат большего из них в 9 раз больше меньшего числа. Найдите эти числа.

2. Одну сторону квадрата увеличили на 2 см, а другую – на 1 см и получили прямоугольник с площадью 12 см². Найдите длину стороны квадрата. Изобразите квадрат и прямоугольник.

П р и м е ч а н и е. В зависимости от уровня подготовки класса можно сократить содержание проверочной работы до одной задачи.

Р е ш е н и е

В а р и а н т 1

1. Пусть х и (х + 2) – два последовательных чётных числа. Зная, что квадрат большего из них в 9 раз больше меньшего числа, составим уравнение:

(х + 2)² = 9х;

х² + 4х + 4 – 9х = 0;

х² – 5х + 4 = 0;

D = (–5)² – 4 · 1 · 4 = 25 – 16 = 9; D > 0; 2 корня.

x₁ = 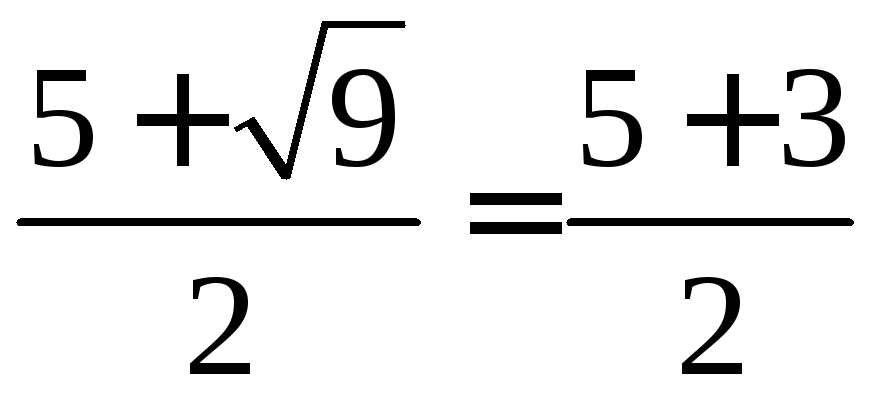= 4;

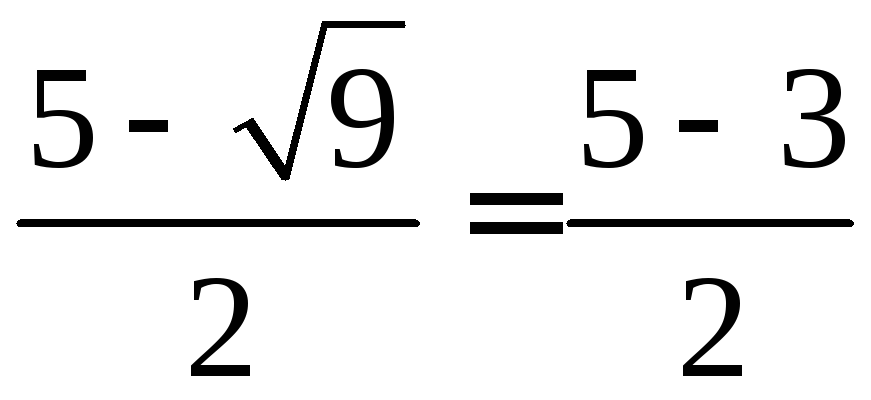x₂ = = 1.

Так как число – чётное, то х₂ = 1 – не удовлетворяет условию задачи.

О т в е т: 4; 6.

2. Пусть х см – сторона квадрата, тогда (х – 2) см и (х – 1) см – стороны прямоугольника. Зная, что площадь полученного прямоугольника равна 6 см, составим уравнение:

(х – 2) (х – 1) = 6;

х² – х – 2х + 2 – 6 = 0;

х² – 3х – 4 = 0;

D = (–3)² – 4 · 1 · (–4) = 9 + 16 = 25; D > 0; 2 корня.

x₁ = 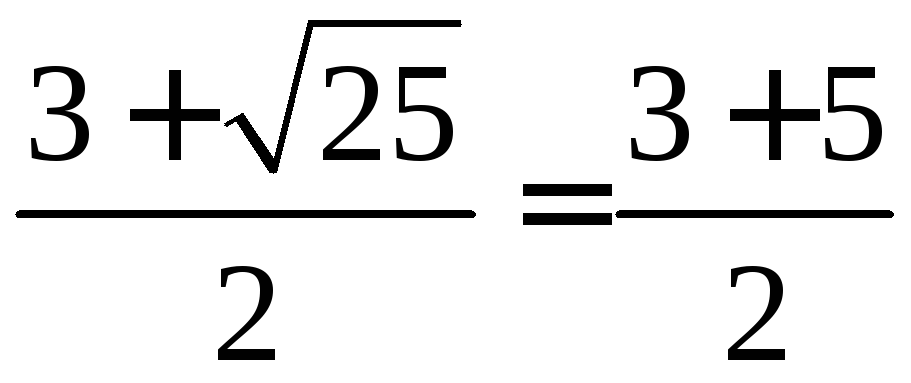= 4;

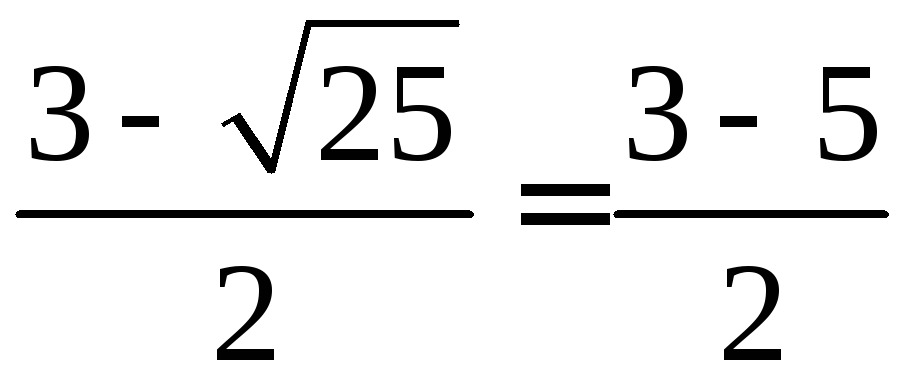x₂ = = –1.

Так как сторона квадрата выражается положительным числом, то х₂ = –1 – не удовлетворяет условию задачи.

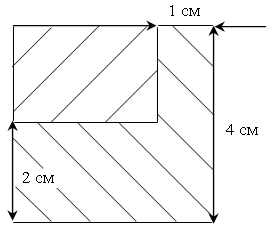
О т в е т: 4 см.

В а р и а н т 2

1. Пусть х и (х + 2) – два последовательных нечётных числа. Зная, что квадрат большего из них в 9 раз больше меньшего числа, составим уравнение:

(х + 2)² = 9х;

х² + 4х + 4 – 9х = 0;

х² – 5х + 4 = 0;

D = (–5)² – 4 · 1 · 4 = 25 – 16 = 9; D > 0; 2 корня.

x₁ = 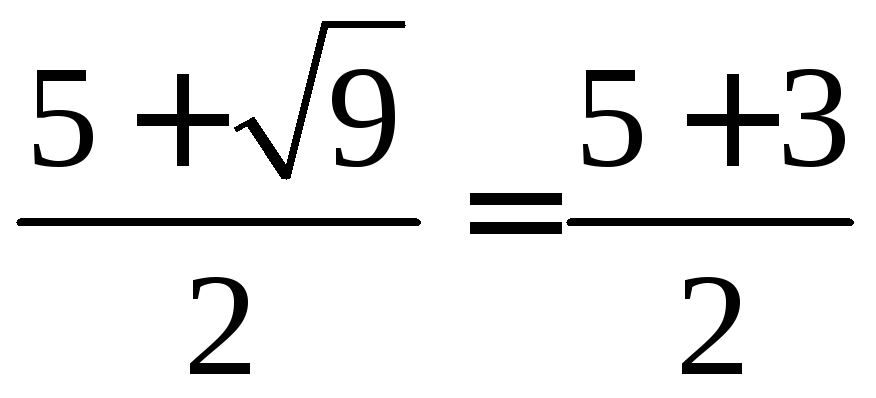= 4;

x₂ = = 1.

Так как число – нечётное, то х₁ = 4 – не удовлетворяет условию задачи.

О т в е т: 1; 3.

2. Пусть х см – сторона квадрата, тогда (х + 2) см и (х + 1) см – стороны прямоугольника. Зная, что площадь полученного прямоугольника равна 12 см, составим уравнение:

(х + 2) (х + 1) = 12;

х² + х + 2х + 2 – 12 = 0;

х² + 3х – 10 = 0;

D = 3² – 4 · 1 · (–10) = 9 + 40 = 49; D > 0; 2 корня.

x₁ = 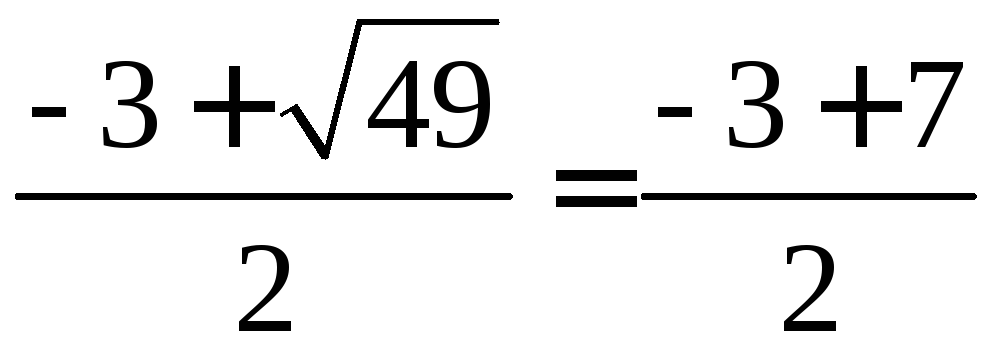= 2;

x₂ = = –5.

Так как сторона квадрата выражается положительным числом, то х₂ = –5 – не удовлетворяет условию задачи.

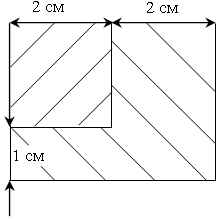
О т в е т: 2 см.

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Какие этапы выделяют при решении задачи алгебраическим методом?

– В чём состоит интерпретация полученного решения задачи?

– Когда полученное решение может противоречить условию задачи?

– Какие решения, полученные на сегодняшнем уроке, вы интерпретировали как противоречащие условию задачи?

Домашнее задание: № 569, № 572, № 574, № 578 (б).

У р о к 1 (52) Доказательство теоремы Виета и её применение

Цели: изучить теорему Виета; формировать умение применять теорему Виета и обратную ей теорему при решении приведённых квадратных уравнений.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите полные, неполные и приведённые квадратные уравнения:

а) 3х² – 2х = 0; е) –21х² + 16х = 0;

б) 7х² – 16х + 4 = 0; ж) х² = 0;

в) х² – 3 = 0; з) х² + 4х + 4 = 0;

г) –х² + 2х – 4 = 0; и) х² = 4;

д) 2 – 6х + х² = 0; к) –7х² + 6 = 0.

2. Преобразуйте квадратное уравнение в приведённое:

а) 3х² + 6х – 12 = 0; г) х² + х – 2 = 0;

б) 2х² = 0; д) 3х² – 7 = 0;

в) –х² – 2х + 16 = 0; е) –5х² + 10х – 2 = 0.

III. Объяснение нового материала.

Объяснение проводится в н е с к о л ь к о э т а п о в.

1. «О т к р ы т и е» теоремы Виета.

Целесообразно организовать лабораторную исследовательскую работу. Для этого разбить класс на пять групп, каждой из которых дать решить приведённое квадратное уравнение. После его решения один представитель от каждой группы выходит к доске и заполняет соответствующую строку в таблице:

Уравнение	b	c	Корни	Сумма корней	Произведение корней
х^2– 3х+ 12 = 0
х^2–х– 12 = 0
х^2+ 5х+ 6 = 0
х^2+ 3х– 10 = 0
х^2– 6х– 7 = 0

После этого учитель предлагает учащимся сравнить сумму и произведение полученных корней с коэффициентами b и c и выдвинуть гипотезу. Учитель подтверждает сделанное предположение, сообщая, что данное утверждение называется теоремой Виета, обращая внимание учащихся, что эта теорема справедлива для приведенных квадратных уравнений.

Можно привести краткий исторический материал о жизни и деятельности Франсуа Виета.

Рассмотреть доказательство теоремы можно как по учебнику (с. 127– 128), так и привлекая учащихся, поскольку оно не является сложным. После доказательства на доску выносится запись:

Т е о р е м а В и е т а

Если х₁, х₂ – корни уравнения x² + px + q = 0,

то х₁ + х₂ = –р; х₁ · х₂ = q.

Для первичного усвоения теоремы Виета можно предложить учащимся выполнить устно упражнение на нахождение суммы и произведения корней квадратного уравнения:

1) № 580 (а, б, в, г) – устно.

2) х² – х – 5 = 0.

3) х² + 3х + 5 = 0.

При выполнении этого задания необходимо предотвратить формальное применение теоремы Виета. Нужно убедиться, что квадратное уравнение имеет корни. Если учащиеся сами не выскажут эту мысль, то при решении третьего задания предложить им найти дискриминант уравнения и сделать соответствующий вывод.

2. Т е о р е м а В и е т а для неприведённого квадратного уравнения.

При выполнении устной работы в начале урока учащиеся вспомнили, как преобразовать квадратное уравнение в приведённое. Следует предложить им самостоятельно вывести формулы для неприведённого квадратного уравнения, используя теорему Виета. После этого на доску выносится запись:

Т е о р е м а В и е т а

Если х₁, х₂ – корни уравнения аx² + bx + c = 0,

то х₁ + х₂ = ;х₁ ∙ х₂ = .

3. Т е о р е м а, обратная теореме Виета.

Обращаем внимание учащихся, что по теореме Виета мы можем только убедиться в правильности нахождения корней с помощью дискриминанта. Возникает вопрос, а если мы подберем такие числа, которые в сумме будут равны второму коэффициенту с противоположным знаком, а в произведении – свободному члену, то не будут ли они являться корнями уравнения? Подчеркиваем, что мы хотим воспользоваться утверждением, обратным теореме Виета, значит, мы должны его доказать. Работа с теоремой Виета и обратной ей теоремой позволяет формировать элементы математической культуры учащихся.

После рассмотрения (по учебнику) доказательства теоремы привести примеры нахождения корней квадратного уравнения подбором.